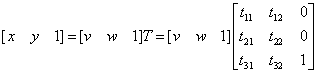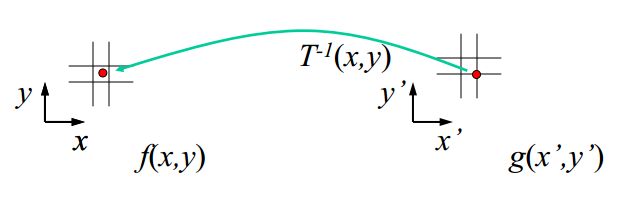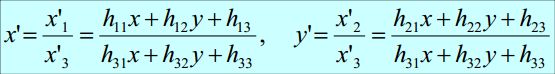图像仿射变换及图像扭曲(Image Warping)
空间图像几何变换包括两个主要步骤:
(1) 空间坐标变换
(2)变换坐标的赋值、插值运算
空间坐标变换一般可以表达为如下式子:
![]()
对于用得普遍的仿射变换,可以表达为如下式子:
(x, y)为变换后的坐标,(v, w)为变换前的坐标。通过变换矩阵T,可以进行图像的缩放,旋转,平移等。有了坐标的变换,下面一步就是进行像素灰度级的赋值了。从原始图像映射到变换图像,赋值的时候需要进行插值运算。通常情况下有三种插值运算:最邻近插值法、双线性插值法、双三次插值法。
在仿射变换的一般表达式中,有两种基本的变换方法。第一种是forward mapping, 第二种 是inverse mapping(backward mapping)。在inverse mapping 中,(v, w) = T¬-1(x, y)。一般情况下,inverse mapping 比forward mapping更有效。仿射变换的原始坐标中,首先将原坐标变换为齐次坐标(齐次坐标的理解)。并且经过仿射变换后,你有了图像插值的基础,这样你就可以学习Image Warping了。姑且翻译为图像扭曲吧。Image Warping 同时也分为 Forward Warping 和 Backward Warping。下面一一介绍:
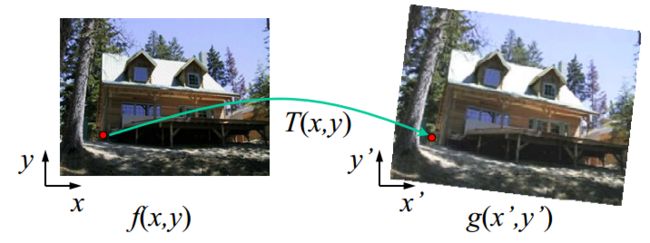
Image Warping:
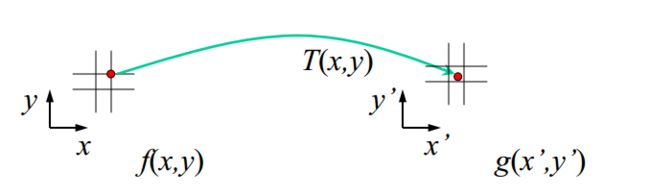
和Mapping一样,都是从原始图像向目标图像映射。其中(x’,y’)= T(x,y),x,y为原始图像坐标。同理,作为Backward Warping则为相反的方向。
其中,(x,y) =inverse(T (x’,y’))。就是从目标图像向原始图像进行映射了。
对于这两种方法,那么哪一种的效果比较好呢?如果实验一下,就会知道,Backward Warping效果比Forward Warping效果好。Forward Warping容易产生空洞及像素的重叠,使其结果不理想。
我想原理还是不难理解的。但是如果我们真正要动手去实现这个个东西,仔细想想,还是缺点什么?那就是缺少变换函数(变换矩阵),就像文章前面提到的仿射变换需要变换矩阵T,那么我们这里需要的是变换矩阵H,英文叫Homography,单应矩阵。如果已经有幅图像,只需要找到原始图像中的任意四个点坐标(其中至少三个点不在同一条直线上),并且指定目标图像中的四个点,这样通过这八个点,就能求出变换矩阵H。由于楼主只实验了Backward Warping,所以下面以Backward Warping为例子进行说明,Forward Warping与其类似,但是变换方向不一样,自然H的方向就不一样。具体过程如下:
变换矩阵H是3X3,根据对其次坐标的理解,H的最后一个元素始终为1,又由于只需要各四个点,所以可以看到最后只取到了h32。并且x,y全部已知,可以通过最小二乘方法求取H:
最后,再在得到的H中,根据齐次坐标的概念,求得最终映射的坐标点:
注意,h33 = 1。
下面贴出Backward Warping的Matlab代码:
%Backward warping
I = imread('X.jpg'); %reference image
I=rgb2gray(I);
I_r = imread('original.jpg');
I_r = rgb2gray(I_r);
[Rows Cols d1] = size(I_r);
figure(1)
imshow(I_r);
title('original image');
figure(2)
imshow(I);
title('reference image');
changeCoordinates=[36,39;618,43;616,285;39,288];
originalCoordinates=[27,13;546,101;550,294;28,330];
A=[];
A1=[originalCoordinates(1,1),originalCoordinates(1,2),1,0,0,0,(-1)*originalCoordinates(1,1)*changeCoordinates(1,1),(-1)*originalCoordinates(1,2)*changeCoordinates(1,1)];
A2=[0,0,0,originalCoordinates(1,1),originalCoordinates(1,2),1,(-1)*originalCoordinates(1,1)*changeCoordinates(1,2),(-1)*originalCoordinates(1,2)*changeCoordinates(1,2)];
A3=[originalCoordinates(2,1),originalCoordinates(2,2),1,0,0,0,(-1)*originalCoordinates(2,1)*changeCoordinates(2,1),(-1)*originalCoordinates(2,2)*changeCoordinates(2,1)];
A4=[0,0,0,originalCoordinates(2,1),originalCoordinates(2,2),1,(-1)*originalCoordinates(2,1)*changeCoordinates(2,2),(-1)*originalCoordinates(2,2)*changeCoordinates(2,2)];
A5=[originalCoordinates(3,1),originalCoordinates(3,2),1,0,0,0,(-1)*originalCoordinates(3,1)*changeCoordinates(3,1),(-1)*originalCoordinates(3,2)*changeCoordinates(3,1)];
A6=[0,0,0,originalCoordinates(3,1),originalCoordinates(3,2),1,(-1)*originalCoordinates(3,1)*changeCoordinates(3,2),(-1)*originalCoordinates(3,2)*changeCoordinates(3,2)];
A7=[originalCoordinates(4,1),originalCoordinates(4,2),1,0,0,0,(-1)*originalCoordinates(4,1)*changeCoordinates(4,1),(-1)*originalCoordinates(4,2)*changeCoordinates(4,1)];
A8=[0,0,0,originalCoordinates(4,1),originalCoordinates(4,2),1,(-1)*originalCoordinates(4,1)*changeCoordinates(4,2),(-1)*originalCoordinates(4,2)*changeCoordinates(4,2)];
A=[A1;A2;A3;A4;A5;A6;A7;A8];
bv=[changeCoordinates(1,:),changeCoordinates(2,:),changeCoordinates(3,:),changeCoordinates(4,:)]';% b
h=pinv(A)*bv; % pinv(A) = (A'A)`A' A'=A^T X`=X^(-1) % Least Square Method
%h=((A'*A)^-1)*A'*bv;
% H=[h(1),h(2),h(3);h(4),h(5),h(6);h(7),h(8),1];
H=[h(1),h(2),h(3);h(4),h(5),h(6);h(7),h(8),1]
H=inv(H);
img_final=[];
M=zeros(Rows,Cols);
X=zeros(3,1);
for j=1:Rows
for i=1:Cols
X = H*[i;j;1];
X=X/X(3);
original_x=X(1);
original_y=X(2);
original_x = round(original_x);
original_y = round(original_y);
if original_x<1 || original_y<1 || original_x >Cols || original_y>Rows
continue;
end
M(j,i) = I_r(original_y, original_x);
end
end
% M = uint8(M);
for j=1:Rows %y
for i=1:Cols %x
% b1=M(0,0);
% b2=M(1,0)-M(0,0);
% b3=M(0,1)-M(0,0);
% b4=M(0,0)-M(1,0)-M(0,1)+M(1,1);
% % M(j,i)=b1+b2*i+b3*j+b4*j*i;
X1 = H*[i;j;1];
X1=X1/X1(3);
if X1(1)<1 || X1(1)>Rows || X1(2)<1 || X1(2)>Cols
continue;
end
b = fix(X1);
k=X1-b;
val=M(b(1), b(2))*(1-k(1))*(1-k(2)) ...
+ M(b(1), b(2)+1)*k(2)*(1-k(1)) ...
+ M(b(1)+1, b(2))*(1-k(2))*k(1) ...
+ M(b(1)+1, b(2)+1)*k(1)*k(2);
X1=fix(X1);
img_final(i,j) = val;
end
end
img_final=uint8(img_final);
figure(3)
imshow(img_final);代码最后做了 双线性内插的,保证得到的图像更平滑。实验图片的来源起始很简单,就是用手机在一个建筑物面前正面照一张,手机横向侧着照一张。然后,分别找出建筑物四个相同特征分别在两幅图中的位置,这样就得到了八个点的坐标。
同时,用OpenCV里面的Warping函数试了一下,测试代码和结果如下:(VS2010 + OpenCV2.4.9.0)
#include <iostream>
#include "cv.h"
#include "highgui.h"
using namespace std;
using namespace cv;
int main(int argc, char**argv)
{
char* source_window = "Source Image";
char* warp_window = "Warp Image";
char* warp_rotate_window = "Warp + Rotate";
Mat src = imread("lena.jpg");
Point2f srcTri[3];
Point2f dstTri[3];
Mat rotMat(2,3,CV_32FC1);
Mat warpMat(2,3,CV_32FC1);
Mat warpDst,warpRotateDst;
warpDst = Mat::zeros(src.rows,src.cols,src.type());
srcTri[0] = Point2f(0, 0);
srcTri[1] = Point2f(src.cols - 1, 0);
srcTri[2] = Point2f(0, src.rows - 1);
dstTri[0] = Point2f(src.cols * 0.0, src.rows * 0.33);
dstTri[1] = Point2f(src.cols * 0.85, src.rows * 0.25);
dstTri[2] = Point2f(src.cols * 0.15, src.rows * 0.7);
warpMat = getAffineTransform(srcTri,dstTri);
warpAffine(src,warpDst,warpMat,warpDst.size());
Point center = Point(warpDst.cols/2,warpDst.rows/2);
double angle = -90.0; //negative - clock-wise
double scale = 0.6;
rotMat = getRotationMatrix2D(center,angle,scale);
warpAffine(warpDst,warpRotateDst,rotMat,warpDst.size(),INTER_CUBIC);
namedWindow(source_window,CV_WINDOW_AUTOSIZE);
imshow(source_window,src);
namedWindow(warp_window,CV_WINDOW_AUTOSIZE);
imshow(warp_window,warpDst);
namedWindow(warp_rotate_window,CV_WINDOW_AUTOSIZE);
imshow(warp_rotate_window,warpRotateDst);
waitKey(0);
return 0;
}原始图像:
Warping结果:
Warping + Rotation结果:
其实突然发现Affine Transform 和Warping的原理好类似,甚至感觉是一个东西,都可以称之为Mapping。只是变换矩阵的不同而已,Warping中还是用了Least Square Method等,但他们都是以齐次坐标理论为基础的。在学习Warping的时候,还看见了一种叫Morphing的东东,它是以Warping为基础的图像变形。那是后话了。。。