极端学习机学习之路----svm的推导过程(精简版)
参考faturo的《SVM入门精品系列讲解目录》和一些别的文档整理而成。
http://www.matlabsky.com/thread-10317-1-1.html
简单来说svm(支持向量机)就是一个分类器,假设有很多点(这些点可以是二维的,也可以使三维空间,甚至是多维的),然后我们要找到一个面(超平面,hyper plane)把这些点分隔开,这个面用下面函数表示:
g(x)=wx+b
我们可以取阈值为0,这样当有一个样本xi需要判别的时候,我们就看g(xi)的值。若g(xi)>0,就判别为类别C1,若g(xi)<0,则判别为类别C2(等于的时候我们就拒绝判断)。此时也等价于给函数g(x)附加一个符号函数sgn(),即f(x)=sgn [g(x)]是我们真正的判别函数。
注:1、x是样本的向量表示,一般要列向量,如果是行向量则要加上转置。
2、并不局限于二维的情况,在n维空间中仍然可以使用这个表达式,只是式中的w成为了n维向量,这里的w严格的说也应该是转置的形式,为了表示起来方便简洁,以下均不区别列向量和它的转置。
如何去确定这个分类面,则如何找个这个函数?这样要引入一个概念:分类间隔。在进行文本分类的时候,每一个样本由一个向量(特征向量)和一个标记(标示属于哪个类别)组成。如下:
Di=(xi,yi)
注:xi就是文本向量(维数很高),yi就是分类标记。
在二元的线性分类中,这个表示分类的标记只有两个值,1和-1(用来表示属于还是不属于这个类)。有了这种表示法,我们就可以定义一个样本点到某个超平面的间隔:
δi=yi(wxi+b)
而δi=yi(wxi+b)=|g(x)|
现在把w和b进行一下归一化,即用w/||w||和b/||w||分别代替原来的w和b,那么间隔就可以写成:
注: ||w||叫做向量w的范数,范数是对向量长度的一种度量。我们常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数,可以写成如下表达式
向量w=(w1,w2, w3,…… wn)
它的p-范数为
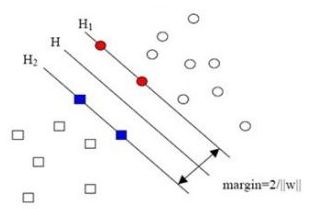
当用归一化的w和b代替原值之后的间隔有一个专门的名称,叫做几何间隔,几何间隔所表示的正是点到超平面的欧氏距离。下面这张图更加直观的展示出了几何间隔的现实含义:
H是分类面,而H1和H2是平行于H,且过离H最近的两类样本的直线,H1与H,H2与H之间的距离就是几何间隔。几何间隔与样本的误分次数间存在关系:
我们的目的是要减少误分次数,即要上面式子的上界变小,即几何间隔δ要越大越好。因为几何间隔δ:
在通常情况下,我们会固定几何间隔(例如固定为1),寻找最小的||w||。用式子表示如下:
min||w||
但实际上对这个目标,我们常常使用另外一个完全等价的目标函数来代替,那就是:
w=α1x1+α2x2+…+αnxn
式子中的αi是一个一个的数(在严格的证明过程中,这些α被称为拉格朗日乘子),而xi是样本点,因而是向量,n就是总样本点的个数。因此g(x)的表达式严格的形式应该是:
g(x)=<w,x>+b
注:<w,x>表示w和x的内积,也叫点积
其实w不仅跟样本点的位置有关,还跟样本的类别有关(也就是和样本的“标签”有关)。因此用下面这个式子表示才算完整:
w=α1y1x1+α2y2x2+…+αnynxn
式子也可以用求和符号简写一下:
如果有这样的函数,那么当给了一个低维空间的输入x以后,
g(x)=K(w,x)+b
f(x’)=<w’,x’>+b
找到核函数后,g(x)的形式可以表示为:
把一个复杂的最优化问题的求解简化为对原有样本数据的内积运算。只需选择适当的核函数及其参数、惩罚因子。