codeforce #200 div2 的水题三道
Mad scientist Mike entertains himself by arranging rows of dominoes. He doesn't need dominoes, though: he uses rectangular magnets instead. Each magnet has two poles, positive (a "plus") and negative (a "minus"). If two magnets are put together at a close distance, then the like poles will repel each other and the opposite poles will attract each other.
Mike starts by laying one magnet horizontally on the table. During each following step Mike adds one more magnet horizontally to the right end of the row. Depending on how Mike puts the magnet on the table, it is either attracted to the previous one (forming a group of multiple magnets linked together) or repelled by it (then Mike lays this magnet at some distance to the right from the previous one). We assume that a sole magnet not linked to others forms a group of its own.
Mike arranged multiple magnets in a row. Determine the number of groups that the magnets formed.
The first line of the input contains an integer n (1 ≤ n ≤ 100000) — the number of magnets. Then n lines follow. The i-th line (1 ≤ i ≤ n) contains either characters "01", if Mike put the i-th magnet in the "plus-minus" position, or characters "10", if Mike put the magnet in the "minus-plus" position.
On the single line of the output print the number of groups of magnets.
6 10 10 10 01 10 10
3
4 01 01 10 10
2
The first testcase corresponds to the figure. The testcase has three groups consisting of three, one and two magnets.
The second testcase has two groups, each consisting of two magnets.
题解:
简单模拟就好,水题~
/****************************>>>>HEADFILES<<<<****************************/
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <sstream>
#include <algorithm>
using namespace std;
/****************************>>>>>DEFINE<<<<<*****************************/
#define fst first
#define snd second
#define root 1,N,1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define PB(a) push_back(a)
#define MP(a,b) make_pair(a,b)
#define CASE(T) for(scanf("%d",&T);T--;)
#define FIN freopen("input.txt","r",stdin)
#define FOUT freopen("output.txt","w",stdout)
//#pragma comment(linker, "/STACK:1024000000,1024000000")
typedef __int64 LL;
const int INF = 0x3f3f3f3f;
/****************************>>>>SEPARATOR<<<<****************************/
int main()
{
// FIN;
int N;
while(~scanf("%d",&N))
{
int ans;string x,prex;
cin>>x;prex = x;
ans = 1;
for(int i = 1;i < N;i++)
{
cin>>x;
if(x!=prex) ans ++;
prex = x;
}
printf("%d\n",ans);
}
}
Mad scientist Mike is busy carrying out experiments in chemistry. Today he will attempt to join three atoms into one molecule.
A molecule consists of atoms, with some pairs of atoms connected by atomic bonds. Each atom has a valence number — the number of bonds the atom must form with other atoms. An atom can form one or multiple bonds with any other atom, but it cannot form a bond with itself. The number of bonds of an atom in the molecule must be equal to its valence number.
Mike knows valence numbers of the three atoms. Find a molecule that can be built from these atoms according to the stated rules, or determine that it is impossible.
The single line of the input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 106) — the valence numbers of the given atoms.
If such a molecule can be built, print three space-separated integers — the number of bonds between the 1-st and the 2-nd, the 2-nd and the 3-rd, the 3-rd and the 1-st atoms, correspondingly. If there are multiple solutions, output any of them. If there is no solution, print "Impossible" (without the quotes).
1 1 2
0 1 1
3 4 5
1 3 2
4 1 1
Impossible
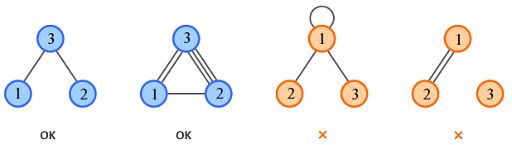
The first sample corresponds to the first figure. There are no bonds between atoms 1 and 2 in this case.
The second sample corresponds to the second figure. There is one or more bonds between each pair of atoms.
The third sample corresponds to the third figure. There is no solution, because an atom cannot form bonds with itself.
The configuration in the fourth figure is impossible as each atom must have at least one atomic bond.
题解:
简单二分~画图出来输入三个数a,b,c;那么有:
a= x + (a - x);
b= x + (b - x);
c= (a – x) + (b - x);
这样:可得 2*x = a+ b - c;
那么对x二分即可~
/****************************>>>>HEADFILES<<<<****************************/
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <sstream>
#include <algorithm>
using namespace std;
/****************************>>>>>DEFINE<<<<<*****************************/
#define fst first
#define snd second
#define root 1,N,1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define PB(a) push_back(a)
#define MP(a,b) make_pair(a,b)
#define CASE(T) for(scanf("%d",&T);T--;)
#define FIN freopen("input.txt","r",stdin)
#define FOUT freopen("output.txt","w",stdout)
//#pragma comment(linker, "/STACK:1024000000,1024000000")
typedef __int64 LL;
const int INF = 0x3f3f3f3f;
/****************************>>>>SEPARATOR<<<<****************************/
int main()
{
// FIN;
int a, b, c;
while(~scanf("%d %d %d", &a, &b, &c))
{
int ans = 0;
int l = 0, r = a + 1, mid;
while(r - l >= 1)
{
mid = l + ((r - l) >> 1);
if(2 * mid < b + a - c)
ans = l = mid + 1;
else if(2 * mid > b + a - c)
ans = r = mid - 1;
else
{
ans = mid;
break;
}
// printf("%d %d %d\n",l,mid,r);
}//puts("");
if(ans < 0 || b - ans < 0 || a - ans < 0 || 2 * ans != b + a - c) printf("Impossible\n");
else printf("%d %d %d\n", ans, b - ans, a - ans);
}
}
Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.
However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:
- one resistor;
- an element and one resistor plugged in sequence;
- an element and one resistor plugged in parallel.
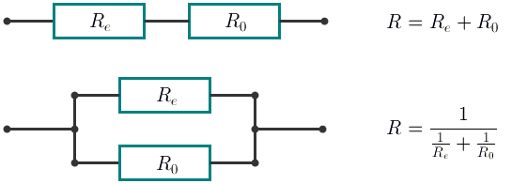
With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals . In this case Re equals the resistance of the element being connected.
Mike needs to assemble an element with a resistance equal to the fraction . Determine the smallest possible number of resistors he needs to make such an element.
The single input line contains two space-separated integers a and b (1 ≤ a, b ≤ 1018). It is guaranteed that the fraction is irreducible. It is guaranteed that a solution always exists.
Print a single number — the answer to the problem.
Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%I64d specifier.
1 1
1
3 2
3
199 200
200
In the first sample, one resistor is enough.
In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance ![]() . We cannot make this element using two resistors.
. We cannot make this element using two resistors.
题解:
题意:用最少的1Ω电阻拼出指定阻值(a/b)电阻.元件之间可以以串联或并联的方式连接.
分析: 显然电阻越并越小,a/b的整数部分可以串联若干1Ω电阻解决.此时,有这样一条重要结论:如果最少用K个电阻构成a/bΩ电阻,那么b/a也需K个(只需改变所有的串并联关系即可).所以此时若b>a,只需交换a,b的值,重复上一步骤.
/****************************>>>>HEADFILES<<<<****************************/
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <sstream>
#include <algorithm>
using namespace std;
/****************************>>>>>DEFINE<<<<<*****************************/
#define fst first
#define snd second
#define root 1,N,1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define PB(a) push_back(a)
#define MP(a,b) make_pair(a,b)
#define CASE(T) for(scanf("%d",&T);T--;)
#define FIN freopen("input.txt","r",stdin)
#define FOUT freopen("output.txt","w",stdout)
//#pragma comment(linker, "/STACK:1024000000,1024000000")
typedef __int64 LL;
const int INF = 0x3f3f3f3f;
/****************************>>>>SEPARATOR<<<<****************************/
int main()
{
//FIN;
LL a, b;
while(~scanf("%I64d %I64d", &a, &b))
{
LL ans = 0;
while(b != 0)
{
ans += a / b;
a %= b;
swap(a,b);
}
printf("%I64d\n",ans);
}
}