UVa 10173 - Smallest Bounding Rectangle

题目：求包裹平面上已知点的最小面积矩形。

分析：计算几何、凸包、旋转卡壳。最小面积矩形一定存在一条边与凸包共线。（不共线时，可以通过旋转变得更小）

            根据以上结论，直接枚举底边，然后利用旋转卡壳确定其余三个顶点即可。

              

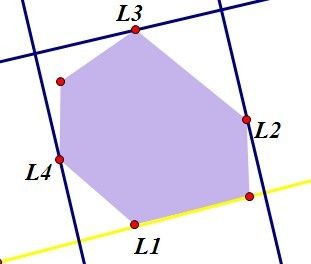
             如图：L1为底边，初始化确定四个边界点，然后利用向量，控制L2，L3，L4与L1的角度即可。

注意：1.输入点可以小于3个，可能是点或者线段；

            2.精度问题，之前用点到直线距离公式WA了N久，换成向量计算就AC了。

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cmath>

#define esp 1e-6

using namespace std;

//点结构 
typedef struct pnode
{
	double x,y,d;
	pnode( double a, double b ){x = a;y = b;}
	pnode(){}
}point;
point P[ 1005 ];

//直线结构 
typedef struct lnode
{
	double x,y,dx,dy;
	lnode( point a, point b ){x = a.x;y = a.y;dx = b.x-a.x;dy = b.y-a.y;}
	lnode(){}
}line;

//叉乘ab*ac 
double crossproduct( point a, point b, point c )
{
	return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y); 
}

//点到点距离 
double dist( point a, point b )
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
} 

//点到直线距离 
double dist( point p, point a, point b )
{
	return fabs(crossproduct( p, a, b )/dist( a, b ));
} 

//坐标排序 
bool cmp1( point a, point b )
{
	return (a.x == b.x)?(a.y < b.y):(a.x < b.x);
}

//级角排序 
bool cmp2( point a, point b )
{
	double cp = crossproduct( P[0], a, b );
	if ( cp == 0 ) return a.d < b.d;
	else return cp > 0;
}

//叉乘判断平行  
double judge1( point a, point b, point c, point d )  
{  
    return crossproduct( a, b, point( a.x+d.x-c.x, a.y+d.y-c.y ) );
}  

//点乘判断垂直 
double judge2( point a, point b, point c, point d )
{
	return ((b.x-a.x)*(d.x-c.x)+(b.y-a.y)*(d.y-c.y));
} 

double Graham( int n )
{
	if ( n < 3 ) return 0.0;
	sort( P+0, P+n, cmp1 );
	for ( int i = 1 ; i < n ; ++ i )
		P[i].d = dist( P[0], P[i] );
	sort( P+1, P+n, cmp2 );
	
	//计算凸包 
	int top = 1;
	for ( int i = 2 ; i < n ; ++ i ) {
		while ( top > 0 && crossproduct( P[top-1], P[top], P[i] ) < esp ) -- top;
		P[++ top] = P[i];
	}
	P[++ top] = P[0];
	if ( top < 3 ) return 0.0;
	
	//旋转卡壳
	int L2 = 0,L3 = 0,L4 = 0;
	for ( int i = 0 ; i < top ; ++ i ) {
		if ( P[i].y <= P[L2].y ) L2 = i;
		if ( P[i].x >= P[L3].x ) L3 = i;
		if ( P[i].y >= P[L4].y ) L4 = i;
	}
	
	double Min = (P[0].x-P[L3].x)*(P[L2].y-P[L4].y);
	for ( int L1 = 0 ; L1 < top ; ++ L1 ) {
		
		//旋转平行边 
		while ( judge1( P[L1], P[L1+1], P[L3], P[L3+1] ) > esp )
            L3 = (L3+1)%top;
		
		//旋转垂直边 
		while ( L2 != L3 && judge2( P[L1], P[L1+1], P[L2], P[L2+1] ) > esp ) 
			L2 = (L2+1)%top;
		while ( L4 != L1 && judge2( P[L1+1], P[L1], P[L4], P[L4+1] ) > esp ) 
			L4 = (L4+1)%top;
		
		double D = dist( P[L3], P[L1], P[L1+1] );
		double L = dist( P[L2], P[L4], point( P[L4].x-P[L1+1].y+P[L1].y, P[L4].y+P[L1+1].x-P[L1].x ) );
		if ( Min > D*L ) Min = D*L;
	}
	return Min;
}

int main()
{
	int n;
	while ( ~scanf("%d",&n) && n ) {
		for ( int i = 0 ; i < n ; ++ i )
			scanf("%lf%lf",&P[i].x,&P[i].y);
		
		printf("%.4lf\n",Graham( n ));
	}
	return 0;
}