Java数据类型(上)
一、java数据类型图如下
二、java基本数据类型讲解以及取值范围
(一)整数类型
1、byte类型
byte在计算机中是占8位的,而且byte是有符号整形,用二进制表示时候最高位为符号位0代表正数1代表负数。默认是0。
取值范围:-128到127(-2的7次方到2的7次方减1)
扩展(取值范围计算):
正数在计算机中是以原码形式存在的,负数在计算机中是以其补码形式存在的,就是负数的绝对值的原码转为二
进制再按位取反后加1。
我们来看-128绝对值128的二进制表示:1000 0000按位取反0111 1111加1后:1000 0000,也就是说-128在计算机
中的表示就是1000 0000了,再来看一下-129在计算机中的表示绝对值129的范围已经超出了了byte的位
数。所以要注意这类问题。
2、short类型
short(短整型)一个short 16位,取值范围为-32768~32767,在内存中占用2个字节(-2的15次方到2的15次方-1)默认是0
3、int类型
int(整型)一个int 32位,取值范围为(-2147483648~2147483647),在内存中占用4个字节(-2的31次方到2的31次方-1)默认是0
4、long类型
long(长整型)一个long 64位,取值范围为(-9223372036854774808~9223372036854774807),在内存中占用8个字节(-2的63
次方到2的63次方-1)默认是0L或0l推荐用大写。
可以看到byte和short的取值范围比较小,而long的取值范围太大,占用的空间多基本上int可以满足我们的日常的计算了,而且
int也是使用的最多的整型类型了。在通常情况下,如果JAVA中出现了一个整数数字比如35,那么这个数字就是int型的,但是如果要表
示long型的就一定要在数据后面加"L"。
byte深入测试(其他类型同理):
public static void main(String[] args) {
/**
* byte类型赋值问题: 负数需要在数值类型前加“-”,如果不标明则说明是正数(-表示负数,+表示正数,+可省略)
* 数值(正数或负数)首位没有0,则默认为十进制 数值(正数或负数)首位包含0(除0x为首位的情况),则表明为八进制(如:011)
* 数值(正数或负数)首位包含0x,则表明为十六进制(如:0x11或0X11)
* 将八进制、十进制、十六进制强制类型转换成byte类型,会丢失精度,byte取值范围为:-128到127
*/
// 八进制(十进制为9),该值输出为9
byte byte_bajinzhi = 011;
// 八进制(十进制为-9),该值输出为-9
byte byte_bajinzhi_fushu = -011;
// 八进制(十进制为585,超出byte取值范围),该值输出结果为,十进制为73(0111八进制)
byte byte_bajinzhi_zhuanhuan = (byte) 01111;
// 十进制,该值输出结果不变为111
byte byte_shijinzhi = 111;
// 十进制,超过byte取值范围,此值输出结果为-127
// 注意:正数在计算机的存储就是此正数的原码;负数在计算机的存储为负数的绝对值的原码转为二进制再按位取反后加1
// 计算过程:129在计算机存储的,原码为:127+2(10000001)(说明:127为01111111,加2后10000001,
// 10000001为计算机的存储,可以看出此值为负数,将首位1去掉,转换来打印到控制台,转换方式:先减1,为0000000,然后按位取反得1111111(127),则最后输出结果为-127)
byte byte_shijinzhi_zhuanhuan = (byte) 129;
// 十六进制(十进制为17),该值输出为17
byte byte_shiliujinzhi = 0x11;
// 八进制(十进制为-17),该值输出为-17
byte byte_shiliujinzhi_fushu = -0x11;
System.out.println("byte_bajinzhi:" + byte_bajinzhi);
System.out.println("byte_bajinzhi:" + byte_bajinzhi_fushu);
System.out
.println("byte_bajinzhi_zhuanhuan:" + byte_bajinzhi_zhuanhuan);
System.out.println("byte_shijinzhi:" + byte_shijinzhi);
System.out.println("byte_shijinzhi_zhuanhuan:"
+ byte_shijinzhi_zhuanhuan);
System.out.println("byte_shiliujinzhi:" + byte_shiliujinzhi);
System.out
.println("byte_shiliujinzhi_fushu:" + byte_shiliujinzhi_fushu);
}
测试结果如下:
byte_bajinzhi:9
byte_bajinzhi:-9
byte_bajinzhi_zhuanhuan:73
byte_shijinzhi:111
byte_shijinzhi_zhuanhuan:-127
byte_shiliujinzhi:17
byte_shiliujinzhi_fushu:-17
(二)浮点类型
1、float类型
内存结构如下:
1bit(符号位) 8bits(指数位) 23bits(尾数位)
2、double类型
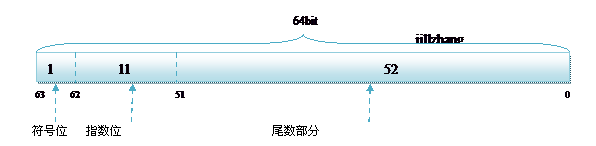
内存结构如下:
1bit(符号位) 11bits(指数位) 52bits(尾数位)
于是,float的指数范围为-128~+127,而double的指数范围为-1024~+1023,并且指数位是按补码的形式来划分的。
其中负指数决定了浮点数所能表达的绝对值最小的非零数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。
float的范围为-2^128 ~ +2^127,也即-3.40E+38 ~ +3.40E+38;double的范围为-2^1024 ~ +2^1023,也即-1.79E+308 ~ +1.79E+308。
3、精度讨论
float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。
float:2^23 = 8388608,一共七位,由于最左为1的一位省略了,这意味着最多能表示8位数: 2*8388608 = 16777216 。有8位有效数字,但绝对能保证的为7位,也即float的
精度为7~8位有效数字;double:2^52 = 4503599627370496,一共16位,同理,double的精度为16~17位。
对于小数来说,更容易会因为精度而出错误。
测试:
测试代码:
float f = 2.2f;
double d = (double) f;
System.out.println(d);
f = 2.25f;
d = (double) f;
System.out.println(d);
测试结果:
2.200000047683716
2.25
------------------------------------------------------------------------------------测试结果分析-----------------------------------------------------------------------------------------------------------------------------
首先我们看看2.25的单精度存储方式,转化为2进制位便是10.01,整理为1.001*2 很简单
于是我们可以写出2.25的内存分布:
符号位为:0
指数为1,用补码表示 0000 0001,转为移码就是1000 0001。
尾数位为0010 0000 0000 0000 0000 000
而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候,数值是不会变的,而我们再
看看2.2呢,2.2用科学计数法表示应该为:将十进制的小数转换为二进制的小数的方法为将小数*2,取整数部分,所以0.282=0.4,所以二进制小数第一位为0.4的整数部分0,0.4×2
=0.8,第二位为0,0.8*2=1.6,第三位为1,0.6×2 = 1.2,第四位为1,0.2*2=0.4,第五位为0,这样永远也不可能乘到=1.0,得到的二进制是一个无限循环的排列 0011001100110011
0011... ,对于单精度数据来说,尾数只能表示24bit的精度,所以2.2的float存储为
但是这样存储方式,换算成十进制的值,却不会是2.2的,因为十进制在转换为二进制的时候可能会不准确,如2.2,而double类型的数据也存在同样的问题,所以在浮点数表示中会产生些许的误差,在单精度转换为双精度的时候,也会存在误差的问题,如下面的代码,输出结果就不一样:
- float f = 2.2f;
- double d = (double) f;
- System.out.println(f);
- System.out.println(d);