LCT学习笔记
一、什么是势能分析?
势能分析首先要有一个势能函数F(S),S是一个数据结构集合,是你要分析的所有数据结构的集合,比如说你要分析一坨splay/lct森林的时间复杂度,那么f就是splay/lct森林的势能函数,而不仅仅是一棵splay/lct,虽然它也可以是。
对于每一次操作,我们进行这样的放缩:实际运行代价+势能改变量 ≤G(n)(n=|S|)。G(n)是一个比较良性的函数。那么我们把所有操作的此式加起来,就有:总运行代价+总势能改变量≤每一次操作的G(n)之和。那么就有总运行代价≤每一次操作的G(n)之和-总势能改变量≤每一操作的G(n)之和的上界-总势能改变量的下界。
二、如何分析splay的时间复杂度?
我们令 F(S)=∑x∈Sf(x),f(x)=logs(x) ,s(x)=以x为根的splay子树的大小。为什么要设这个函数呢?我感觉最主要的原因就是我们希望它的时间复杂度是logn的,其次是对加减操作套以log会让它更易于放缩。
splay的工作方式是当你splay x的时候,检查x的父亲是否是根,如果是的话就把x旋到根;否则的话就看旋转x的父亲和旋转x的方向是否一致,一致的话就先旋x的父亲再选x,否则就旋两次x。
为什么要这么做呢?实际上是因为如果双旋的话操作代价的常数因子是可以被放缩掉的。根据上文所述,我们需要考虑的是每一次旋转的势能改变量+1(大小没有关系,只是表示它是个常数)。
设一次旋转后的f(x)为f’(x),旋转前的还叫f(x).
我们对三种情况分别考虑。
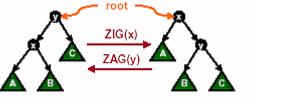
f′(x)+f′(y)−f(x)−f(y)+1=f′(y)−f(x)+1≤f′(x)−f(x)+1
f′(x)+f′(y)+f′(z)−f(x)−f(y)−f(z)+2
(+2是为了下面方便化式子,常数而已。)
≤f′(y)+f′(z)−2f(x)+2≤2(f′(x)−f(x))+2+(f′(y)−f′(x))+(f′(z)−f′(x))
(化出我们期望得到的形式:
Δf(x) )
=2(f′(x)−f(x))+2+logs′(y)s′(x)s′(z)s′(x)≤2(f′(x)−f(x))+2+logs′(y)s′(x)+s′(z)s′(x)22
(均值不等式)
=2(f′(x)−f(x))+2+2logs′(y)+s′(z)2s′(x)≤2(f′(x)−f(x))+2−2∗(−1)
(看图可知)
=2(f′(x)−f(x))
(于是我们惊奇的发现,旋转花费的代价被放缩掉了)
f′(x)+f′(y)+f′(z)−f(x)−f(y)−f(z)+2=f′(y)+f′(z)−f(y)−f(x)+2≤f′(x)+f′(z)−2f(x)+2
(凑出f’(x)和两个儿子覆盖ABCD的节点,以便均值不等式放缩出2)
≤3(f′(x)−f(x))+2+(f′(z)−f′(x))+(f(x)−f′(x))=3(f′(x)−f(x))+2+logf′(z)f′(x)f′(x)f(x)
(与zigzag类似)
≤3(f′(x)−f(x)+2−2
(同样看图易知)
=3(f′(x)−f(x))
显然每次旋转f(x)都是增大的,那么我们将一次splay中每次旋转的代价加势能改变量加起来就会发现它 ≤3(f′(x)−f(x))+1≤3logn+1
所以G(n)的和的上界是nlogn,而显然 F(S)∈[0,nlogn] ,所以 ΔF(S)≥−nlogn ,所以splay的总时间复杂度就是nlogn的。
三、lct的时间复杂度
lct的所有操作都依赖于access操作,我们也许也会在lct中单独splay,但那些操作我们只需套用splay的时间复杂度分析即可。所以lct的时间复杂度分析就是对于access的时间复杂度分析。
我们称lct的splay中的边为关键边。
首先我们来分析一下关键边与非关键边之间的转换次数,它显然就等于splay次数。在这里我们需要使用树链剖分中的轻重边的概念,即x连向它s函数值(子树大小)最大的儿子的边我们称之为重边,其余的边成为重边。显然,任意一个节点到根的路径上最多只有logn条轻边,因为考虑从节点x向上走,没遇到一条轻边,就意味其子树大小至少*2。
那么access过程中,至多也只会将logn条轻边由非关键边变为关键边。但是会改变多少条重边呢?显然,如果一开始每一个节点都是一个单独的lct的话,那么重边变为关键边的次数就至多为重边变为非关键边的次数+1;如果一开始把一条重链建成一个splay,那么重边变为关键边的次数就至多为重边变为非关键边的次数。而一个如果一个重边变为非关键边,就必然意味着一个轻边把它从splay里面挤出来了或者是access了它的一个节点。所以O(重边变为关键边的总次数)=O(轻边变为关键边的总次数)=O(nlogn)。
那么我们再考虑一下一次access中splay的时间复杂度。在这里我们需要换一个势能函数了,我们令s(x)=lct中的子树大小,它定义为 s(x)=∑ys(y) [y是x在splay中的儿子或原树中的儿子]+1。
那么显然,对于每一次splay,使用与分析splay时完全一样的分析可以得到操作数+势能改变量≤3(f’(x)-f(x))+1,我们把若干次splay全加起来就可得到3(f’(x)-f(x))+splay次数。而次数我们已经分析过了是均摊nlogn,而也有 3(f′(x)−f(x))≤3logn ,lct的势能改变量显然也≥-nlogn,所以access总的均摊时间复杂度就是 O(nlogn) 的。
我们再来梳理一遍这是怎么回事:
①轻边在单次操作中只会变成关键边logn次,所以它们变成关键边的总次数至多是nlogn次。
②重边变成关键边意味着之前有一条轻边把它从splay中挤出,所以重边变成关键边的均摊次数等于轻边变成关键边的次数,所以它们变成关键边的次数是O(nlogn)的。
③一次access中若干splay的总时间复杂度是O(nlogn+splay总次数-lct势能改变量),splay总次数上面已经分析过了是O(nlogn)的,而势能改变量根据定义显然也≥-nlogn,所以它的总时间复杂度也是O(nlogn).
四、奇怪向:链剖splay?
使用与lct相同的势能函数,确实可以得到O(nlogn)的均摊时间复杂度。不过与线段树不同的是不能把所有节点都塞进一棵splay里,而是要对于每一个重链维护一棵单独的splay才行。
我感觉对于 n=105 的数据范围,应该会比链剖线段树和lct都快一些吧?并没有试过,不过感觉挺有意思,有时间拿个链剖题试试。
五、吐槽
学lct\splay的时候看了杨思雨的写splay的国家集训队论文,关于时间复杂度用势能分析的部分感觉完全没说清楚,不知道为什么用了一种很奇怪很鬼畜的讲解方式。。膜拜了网上其他人写的blog才明白的。
杨哲写的qtree解题报告讲lct却讲得非常明白非常好。
2014年何琦的国家集训队论文里说splay常数是3(势能分析)* 6(旋转),这显然不太对啊,势能分析出来的应该是 6*(3logn-(-logn))=24logn,常数起码应该是24才对,21是什么鬼啊;然后说lct的常数和splay相同,这更扯淡了,起码应该是nlogn(轻边变关键边)+nlogn(重边变关键边)+6 * (3nlogn+(nlogn+nlogn)(所有边变关键边的次数)-(-nlogn)(势能改变量))=38nlogn,常数38才比较科学,怎么可能跟splay一样呢?
六、实现及实现中可能遇到的问题(我犯的傻逼错误)
1、一定要注意区分lct的根和splay的根。(我习惯叫前者root,后者top)
2、为了方便起见,我们通常需要引入一个换根的操作(我将其称之为makeroot),将u换到根其实意味着u到root的路径上所有节点的父子关系置反,在splay里就是大小关系置反。这导致我们需要存一个翻转标记。
3、access(u)的时候可以在将u接到它的父splay上的时候顺便旋转(rot)一下,这样u就会成为lct的root splay的top。
4、得到一条路径(getchain(u,v))的方式是makeroot(u),access(v),那么u就会成为lct的root,v会成为这条路径的splay的top。
5、如果要维护的是边权信息,就在每条边的中间插一个点,记录这条边的信息。
6、link(u,v)的方式是getchain(u,v),然后将u的父指针指向v。
7、cut(u,v)的方式是getchain(u,v),然后将u的父指针和v的左儿子指针清空。
8、如果是cut一个点的话(cut(u))(把边看成点的时候就会需要这么做)其实就不用那么麻烦了,只需要splay(u),然后将u的左儿子们的父指针指向u的父亲,将u的右儿子清零。
9、常数优化:能splay就不要access。
10、务必要注意splay与线段树的巨大不同:splay需要单独维护节点的信息。
11、其实在静态dfs序中求子树也是可以换根的,如果是在新根和老根之间的节点求其子树的时候就其向新根方向的节点的子树然后对全集求补集就行了。
12、判断(u,v)是否联通?u==v||getchain(u,v),lct[u].fa≠0.一定要小心u==v的情况。。
13、判断(u,v)是否有边直连?getchain(u,v),lct[u].fa&&!lct[u].ch[1]如果u有父亲的话,它必然是v,只需判断u是否有右儿子就行了。
14、改变一个点的孩子信息前一定要先pushdown。
15、splay前一定要下方标记到它的top(而不是root!)
16、做树上的题的时候一定要生成一个链的数据,如果是随机树的话很有可能你并不能发现你写残了,但链很有可能会帮你发现。