枚举法的简单心得

枚举法：

百度百科的解释是：在进行归纳推理时，如果逐个考察了某类事件的所有可能情况，因而得出一般结论，那么这结论是可靠的，这种归纳方法叫做枚举法．

优点：算法简单，容易想到        缺点：时间复杂度高，运算量大，

但是，但是，如果，我们能排除那些明显不属于题解的元素，在局部使用枚举，它的效果是相当非常好的。

ps：下面两个问题均摘自百度,其中第二题的判断条件也是借鉴与热心网友，在此谢谢了

问题1：

百钱买百鸡问题：有一个人有一百块钱，打算买一百只鸡。到市场一看，大鸡三块钱一只，小鸡一块钱三只，不大不小的鸡两块钱一只。现在，请你编一程序，帮他计划一下，怎么样买法，才能刚好用一百块钱买一百只鸡？

代码1：

#include <iostream>
using namespace std;

int main(){
	int x,y,z;      //x,y,z分别表示大鸡，小鸡，不大不小的鸡的个数 
	
	for(x = 0;x<100; x++){
		for(y=0; y<100; y++){
			for(z= 0;z<100;z++){
				if((x+y+z == 100) && (3*x+y/3+ 2*z == 100)  &&  (y%3 == 0))
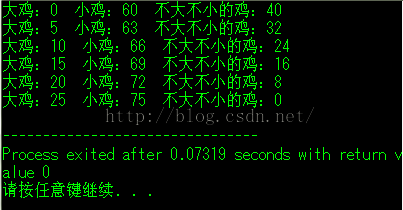
				    cout<<"大鸡："<<x<<"  "<<"小鸡："<<y<<"  "<<"不大不小的鸡："<<z<<endl;
			}
		}
	} 
	return 0;
}

运行结果：

好，我们来看这个程序,它的时间复杂度是100^3，已经特别大，这时我们就可以来考虑在局部使用枚举法

首先大鸡，小鸡，不大不小的鸡总共100，在第一个循环里，已经确定了大鸡的个数，那么我们知道（小鸡最多是100-大鸡的个数），我们确定了小鸡的个数，那就是不大不小的鸡的个数我们都确定了，也就是（大鸡-小鸡-不大不小的鸡）

0k'，我们来看程序：

代码2：

#include <iostream>
using namespace std;

int main(){
	int x,y,z;      //x,y,z分别表示大鸡，小鸡，不大不小的鸡的个数 
	
	for(x = 0;x<100; x++){
		for(y=0; y<100-x; y++){
			    z = 100-x-y;
				if((3*x+y/3+ 2*z == 100)  &&  (y%3 == 0))
				    cout<<"大鸡："<<x<<"  "<<"小鸡："<<y<<"  "<<"不大不小的鸡："<<z<<endl;
			}
	} 
	return 0;
}

运行结果：如上图（代码1的结果）

这时，我们知道;程序的时间复杂度大大减小，O（100^2）,所以我们在用枚举法的时候，一定要注意它的约束条件，这对我们程序执行的时间影响是很大的。

问题2：

将1,2...9共9个数分成三组,分别组成三个三位数,且使这三个三位数构成1:2:3的比例,试求出所有满足条件的三个三位数.

分析：如果我们自己写的话，首先要找到9个数，就意味着我们要9个大for循环，这时候，我相信它的时间复杂度也就爆炸了，

然而，如果我们考虑他们的关系 ，三个数：构成1:2:3的比例，那么结果就大大不一样了。

#include <iostream>
#include <conio.h>
using namespace std;

int check(int , int , int );
int main(){
	int i;
	int a = 0;
	for(i=123; i<321;i++){
		if(check(i,2*i, 3*i)){
			a++;
			printf("%d :  %d   %d  %d\n", a, i, 2*i, 3*i);
		}
	}
}

int check(int a, int b, int c){
	int i =45;    //1+2+3+....+9 = 45; 
	long j = 362880;    //1*2*3*....*9 = 362880;
	int a1 = a%10 + a/10%10 + a/100%10;
	int b1 = b%10 + b/10%10 + b/100%10;
	int c1 = c%10 + c/10%10 + c/100%10;
	
	long a2 = (a%10) * (a/10%10) * (a/100%10);
	long b2 = (b%10) * (b/10%10) * (b/100%10);
	long c2 = (c%10) * (c/10%10) * (c/100%10);
	if((a1 + b1 + c1 ==i)   &&  (a2*b2*c2 == j))
		return 1;
	return 0;
}

程序复杂度极地，大大的降低了O(n)，有利于我们编程，

其中上面程序中的：

是我们判断三个三位数都是不相同的数字的一个很好的判断方法，值得大家的借鉴，如果，让我们写程序可能又是一个很麻烦的过程，

简而言之，也就是三个数的数字之和和数字之积如果都为123456789的和或积的话，也就说明不重复。

程序的最终目的也就是:时间和空间，

尽管枚举的时间复杂度高，但是我们也应该尽可能的缩减枚举的范围（局部枚举），来力求完善自己的程序