hdu 4582 DFS spanning tree
题意:给出一棵dfs生成树,让你选一些树上的边,使得所有T-Simple Circles至少包含一条你选的边。
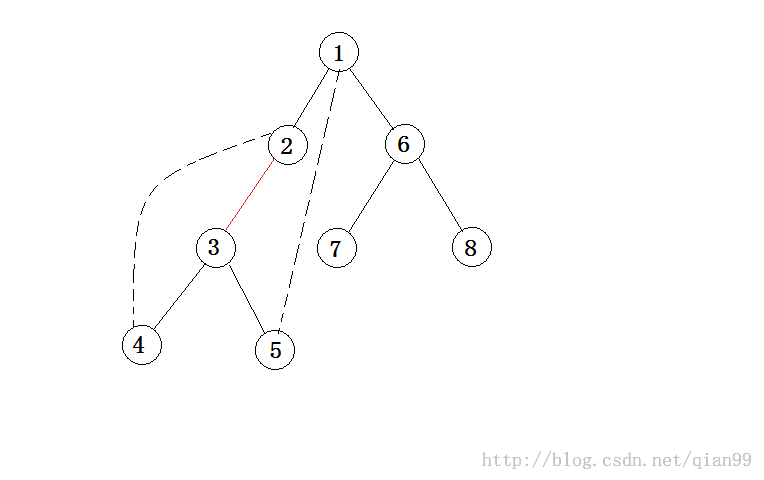
思路:由于给出的是dfs生成树,所以这里是没有横叉边的,直觉告诉我们选择的边应该在树上尽量“高”,对于生出树上的边(u,v),可以考虑这条边是否必须被选择,如果必须被选,那么就选择它,并把v的子树上的点都标记掉,这些点的反向边都包含(u,v)了。
一条边是否必须被选可以看下面的图,(2,3)这条边必须被选当且仅当2有连向其子节点的非树边(如果不是这样,我们总可以找出更"高"的边),并且这个点没有被标记。选择(2,3)这条边以后可以发现,3及其子树中的所有的点连向它们父节点的边都已经包含(2,3)了,因此将它们都标记掉就行了。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#define inf 0x3f3f3f3f
#define Inf 0x3FFFFFFFFFFFFFFFLL
#define eps 1e-9
#define pi acos(-1.0)
using namespace std;
typedef long long ll;
const int maxn=2000+10;
const int maxm=20000+10;
struct Edge
{
int v,next;
};
Edge edges[maxn<<1],ee[maxm<<1];
int head[maxn],h[maxn],nEdge,ne;
int S[maxn],pre[maxn],c,ans,dfs_clock;
bool flag[maxn];
void AddEdge(int u,int v,int wh)
{
if(wh)
{
nEdge++;
edges[nEdge].v=v;edges[nEdge].next=head[u];
head[u]=nEdge;
}
else
{
ne++;
ee[ne].v=v;ee[ne].next=h[u];
h[u]=ne;
}
}
void dfs(int u,int fa)
{
pre[u]=++dfs_clock;
for(int k=head[u];k!=-1;k=edges[k].next)
{
int v=edges[k].v;
if(v==fa) continue;
dfs(v,u);
for(int p=h[u];p!=-1;p=ee[p].next)
{
int to=ee[p].v;
if(!pre[to]) continue;
if(!flag[to]&&pre[to]>=pre[v])
{
ans++;
int tmp=0;
for(int i=0;i<c;++i)
{
if(pre[S[i]]>=pre[v])
flag[S[i]]=true;
else S[tmp++]=S[i];
}
c=tmp;
}
}
}
S[c++]=u;
}
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
int n,m;
while(~scanf("%d%d",&n,&m))
{
if(n==0&&m==0) break;
memset(flag,0,sizeof(flag));
memset(pre,0,sizeof(pre));
memset(head,0xff,sizeof(head));
memset(h,0xff,sizeof(h));
nEdge=ne=-1;
int u,v;
for(int i=1;i<n;++i)
{
scanf("%d%d",&u,&v);
AddEdge(u,v,1);
AddEdge(v,u,1);
}
for(int i=n;i<=m;++i)
{
scanf("%d%d",&u,&v);
AddEdge(u,v,0);
AddEdge(v,u,0);
}
dfs_clock=c=ans=0;
dfs(1,-1);
printf("%d\n",ans);
}
return 0;
}