规则引擎研究(一)——Rete算法(5)——一种产生式的优化算法
一、 简介
产生式系统的系统随着事实数目的增多,性能也跟着下降。因为在大多数的系统中,匹配过程中的连接(join)操作花费的时间与事实数目的平方成正比。另外,不当的条件排列顺序可以产生大量的中间数据,从而导致大量的join操作。
为了解决这个问题,ART、YES/OPS以及其他的一些系统允许用户自己设定join结构。在没有一个专门的优化器来确定join的最佳机构时,专家系统的设计者一般都是采用手动的方式来设定join结构。本文提出了一种优化算法可以减小产生式系统中的join操作的开销。此算法并不是直接将启发式算法用在规则上,而是列举可能的join结构,从而选出最佳结构。主要的思想是采用一些有效约束条件来减少可能结构数目。引入一个代价模型(cost model)来估计在不同join结构中的进行join操作的代价。测试结果显示,采用本算法,可以产生和手动设置一样有效的程序。
二、 Join拓扑结构(topological transformation)
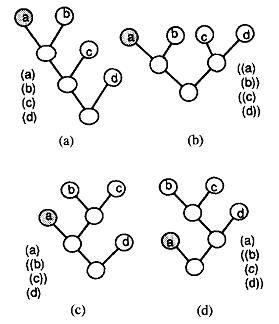
规则的条件可以有多种拓扑结构,如下图所示,条件(a, b, c, d)可以有以下四种结构,如果条件的顺序可变,则join的结构可以达到4*4!=96种。因此,可能的join结构的数目与条件的个数的指数在一个数量级上。
三、 Rete算法特点
Rete算法中的启发式(heuristic)特点有:
3.1 约束性条件优先(place restrictive conditions first)
中间数据(即tokens)所进行的操作占据了总的join操作的绝大部分。减少中间数据的方法之一就是把约束性条件先进行join操作。如下图所示,含有事实越少的alpha内存越优先。

3.2 将易变的规则置后(place volatile conditions last)
假设有N条规则,如果添加(或删除)第一条规则对应的事实,则其余N-1个规则的节点的Join操作到要重复进行。但是,如果此事实对应的规则是第N条,那么只要进行一次join操作。为了减少join操作的次数,把易变的事实对应的规则放在放在后面。如下图所示。

3.3 在规则间共享Join块(share join clusters among rules)
如果某个Join块(join cluser)被N条规则共享,则相当于此join操作的代价降低到原来的1/n。为了获得更大的共享块,一般改变规则的Join结构。如下图所示。
以上启发式算法是rete算法的重要特点。但是,因为不同的启发式算法之间存在冲突,因此专家系统设计者在如何设计一个更好的Join结构时往往要走很多弯路。本文提出的优化算法可以实现join结构的各种拓扑转换,同时自动估计各种结构的性能。

四、 代价模型(cost model)
本文引入的代价模型如下图所示:
在代价模型中,每个节点n都有五个参数:Token(n), Memory(n), Test(n), Cost(n)和Ratio(n)。Token(n)指从节点n传递到其后继节点的所有tokens的数目。Memory(n)指n节点内存中平均存储的tokens数目。Test(n)指n节点总共进行的join测试数目。Cost(n)指在n节点进行的join操作所花费的代价,用一个代价函数来确定。Ration(n)是n节点上join测试成功的比例。
在系统优化时,创建不同的Join结构并且评价其性能。
在开始优化前,产生式系统先运行一边,记录下每个节点的Test(n), Token(n), Memory(n)。
五、 优化算法
正如第三部分所述,启发式算法不能单独应用,因为它们之间可能会有冲突。同时,join结构的可能数目与节点数的指数级是一个数量级的,
因此,产生——测试(generate-and-test)的方法不能解决这个问题。本文中采用不同的约束限制条件来产生可能的Join结构,极大减少了需
要检测的join结构的数目。
5.1 具体算法步骤是:
1、 根据程序的运行确定各个规则的代价大小,按降序排列。从代价最高的规则开始优化。这样保证代价较高的规则有较大的自由度来选
择Join结构。
2、 在优化各个规则前,先把每个alpha节点和beta节点加入到join-list中去。
3、 在优化每个节点时,从Join-list上选择两个节点,创建它们的join节点。如果在join-list没有与新创建的Join结构相同的节点,则
把此节点加入到Join-list中去。
4、 创建每个可能的Join结构后,从中选出最低代价的结构。
5.2 约束条件
上面的算法用到了下面的约束条件来减少可能的join结构数目。
最少代价约束(minimal-cost constraint)
最少代价约束是指,如果某个将要创建的节点比目前Join-list中已存在的节点的代价高,则不创建此节点。形式化定义为,如果满足下面条件
,则不创建s节点:
其中,conditions(s)指s节点的Join结构中的条件集合。
连接约束(connectivity constraint)
连接约束是指,当两个节点之间没有共同变量时,不创建这两个节点的join节点。例如,p, q是规则中的alpha节点。如果满足如下条件,则不
创建l, r的连接节点s:

其中,variables(l)指l的join结构中的变量结合。
在下图所示的例子中,节点b和d不能执行join操作,因为它们之间没有共享变量(满足条件1),同时存在一个c节点,使它们满足条件2。但a,
b可以执行join操作,因为,虽然满足条件1但不满足条件2。
优先级约束
根据统计数据可以确定各个alpha的节点的优先级。优先级约束是指,当进行join操作时,先把优先级高的节点进行Join。更为形式化的定义
:p, q都是alpha节点,且p>q(即p的优先级高于q)。那么不创建l, r的join节点,如果满足如下条件:

上面p>q的定义是当且仅当token(p)>token(q)且memory(p)>memory(q)。引入条件二是为了防止这样一种情况,即,当l和r因为优先级约束不能
Join时,l和p因为连接约束也不能进行join。连接约束和优先级约束可以显著的减少搜索可能范围,但是有可能漏掉在最优结构。
六、 试验结果
把本文所述的优化器用于类似与ops5的系统中。系统配置如下图所示:
实验结果显示,采用优化后,join节点减少到原来的1/3,CPU运行时间减少到原来的1/2,比采用手动优化的效率还高。
不采用优先级约束得到的join结构数目是原来的3.7倍,而同时不使用优先级和连接约束,得到的是原来的6.3倍。根据优化时间与Join结构数
目的平方成正比的规律,优化时间相应的是原来的14到40倍。
本文引入的算法在一个专家系统上测试表明,使用此优化算法同手动优化一样有效。文中提出的代价模型在优化算法中非常重要,但一个完全
精确的模型很难达到。
