数据结构(13)二叉树的动态链表存储和遍历的实现

参考书籍：数据结构（C语言版）严蔚敏吴伟民编著清华大学出版社

1.动态二叉链表存储即遍历的实现

1.1.动态二叉链表的定义

#include<stdio.h>
#include<stdlib.h>
#define NULL 0
typedef char TElemType;
//动态二叉链表
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

测试用例：

测试按先序序列输入：abc..de.g..f...#,点号代表空树，#为输入结束符

另外下面的算法有使用到栈的，栈的相关实现如下：

#define MAXSIZE 100
typedef BiTNode* SElemType;
typedef struct SqStack{
	SElemType data[MAXSIZE];
	int top;//指向栈顶元素
}SqStack;

//初始化空栈
void initStack(SqStack &s){
	s.top = 0;
}

//判栈空
bool isEmpty(SqStack s){
	if(s.top == 0){
		//printf("是空栈\n");//
		return true;
	}else{
		return false;
	}
}

//判栈满
bool isFull(SqStack s){
	if(s.top == MAXSIZE){
		return true;
	}
	else{
		return false;
	}
}

//取栈顶元素
void getTopElem(SqStack s, SElemType &e){
	if(!isEmpty(s))
		e = s.data[s.top-1];
	else
		printf("此栈为空栈，取栈顶元素失败\n");
}

//入栈
void push(SqStack &s, SElemType e){
	if(!isFull(s)){
		s.data[s.top] = e;
		s.top++;
	}else
		printf("此栈已满，入栈操作失败\n");
}

//出栈
void pop(SqStack &s, SElemType &e){
	if(!isEmpty(s)){
		e = s.data[s.top-1];
		s.top--;
	}
	else
		printf("此栈为空栈，出栈操作失败\n");
}

更详细的栈实现请参见我的另一篇博文：数据结构(5)--栈的定义以及相关操作的实现http://blog.csdn.net/u010366748/article/details/50639195

1.2按先序序列输入创建二叉树的递归算法

//利用先序序列建立一颗二叉树，先序序列读入：'a', 'b', 'c', '.', '.', 'd', 'e', '.', 'g', '.', '.', 'f', '.', '.', '.' 
//,'.'代表空树
//测试用例：abc..de.g..f...#
void createBiTreeByPreOrder(BiTree &T){
	//按先序次序输入二叉树中节点的值（一个字符），点号字符表示空树，构造二叉链表表示的二叉树
	//注意：若输入的字符数（不含#号）为n个，则相应的空树即点号就应该有n+1个
	char ch;
	scanf("%c", &ch);
	//printf("test:%c\n", ch);
	if(ch != '#'){
		if(ch == '.'){
			T = NULL;
		}else{
			T = (BiTNode *)malloc(sizeof(BiTNode));
			T->data = ch;
			createBiTreeByPreOrder(T->lchild);
			createBiTreeByPreOrder(T->rchild);
		}
	}
}

1.3先序遍历二叉树的递归算法

//先序遍历打印二叉树的递归算法(根、左、右)
void preOrderPrint(BiTree T){
	if(T){
		printf("%c ", T->data);
		preOrderPrint(T->lchild);
		preOrderPrint(T->rchild);
	}
}

1.4先序遍历二叉树的非递归算法

//先序遍历打印二叉树的非递归算法(根、左、右)
void preOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;	
	while(p || !isEmpty(s)){		
		if(p){
			printf("%c ", p->data);
			push(s, p);
			p = p->lchild;
		}else{
			//printStack(s);
			pop(s, p);//栈顶指针（当前层的根节点指针）弹出
			p = p->rchild;
		}
	}
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	printf("先序遍历打印二叉树:\n");
	preOrderPrint(T);
	printf("\n");
	
	printf("先序遍历打印二叉树（非递归算法）:\n");
	preOrderPrint2(T);
	printf("\n");
}

1.5中序遍历二叉树的递归算法

//中序遍历打印二叉树的递归算法（左、根、右）
void inOrderPrint(BiTree T){
	if(T){
		inOrderPrint(T->lchild);
		printf("%c ", T->data);		
		inOrderPrint(T->rchild);
	}
}

1.6中序遍历二叉树的非递归算法

//中序遍历打印二叉树的非递归算法（左、根、右）
void inOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;	
	while(p || !isEmpty(s)){
		if(p){
			push(s, p);
			p = p->lchild;
		}else{
			pop(s, p);//栈顶指针（当前层的根节点指针）弹出
			printf("%c ", p->data);			
			p = p->rchild;
		}
	}
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	printf("中序遍历打印二叉树:\n");
	inOrderPrint(T);
	printf("\n");
	
	printf("中序遍历打印二叉树（非递归算法）:\n");
	inOrderPrint2(T);
	printf("\n");
}

1.7后序遍历二叉树的递归算法

//后序遍历打印二叉树的递归算法（左、右、根）
void postOrderPrint(BiTree T){
	if(T){
		postOrderPrint(T->lchild);
		postOrderPrint(T->rchild);
		printf("%c ", T->data);
	}
}

1.8后序遍历二叉树的非递归算法

//后序遍历打印二叉树的非递归算法（左、右、根）
void postOrderPrint2(BiTree T){
	SqStack s;
	initStack(s);
	BiTNode *p = T;
	while(p || !isEmpty(s)){
		if(p){
			push(s, p);
			p = p->lchild;
		}else{ 
			BiTNode *top;
			getTopElem(s, top);//取得栈顶元素
			if(top->data > 0){//栈顶元素的右子树还没有被访问过
				p = top->rchild;
				top->data = -top->data;//赋右子树已遍历标志
				
			}else{//栈顶元素的右子树已经访问过了
				printf("%c ", -top->data);
				pop(s, top);
				//p = NULL;				
			}
		}		
	}
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	printf("后序遍历打印二叉树:\n");
	postOrderPrint(T);
	printf("\n");

	printf("后序遍历打印二叉树（非递归算法）:\n");
	postOrderPrint2(T);
	printf("\n");
}

1.9按层次遍历二叉树的非递归算法

typedef BiTNode* QElemType;
typedef struct{
	QElemType data[20];
	int f;//指向队头元素
	int r;//指向对尾元素的下一个位置
}SqQueue;
//初始化一个空队列
void initQueue(SqQueue &Q){
	Q.f = Q.r = 0;
}

//按层次遍历（从上到下，从左到右），
void hierarchicalTraversePrint(BiTree T){
	//QElemType queue[20];//维护一个顺序队列，用来按层次存放每个实节点，实际上是一个广度优先搜索
	//int f = 0, r = 0;//队头队尾
	SqQueue Q;//维护一个顺序队列，用来按层次存放每个实节点，实际上是一个广度优先搜索
	initQueue(Q);
	//注意，不能写成int f, r = 0;否则f没有被赋值
	if(T){
		//queue[0] = T;//根节点入队
		Q.data[Q.r] = T;//根节点入队
		Q.r++;
	}
	while(Q.f != Q.r){
		//先将队头元素的左孩子依次入队
		if(Q.data[Q.f]->lchild){
			Q.data[Q.r] = Q.data[Q.f]->lchild;
			Q.r++;
		}
		//将队头元素的右孩子依次入队
		if(Q.data[Q.f]->rchild){
			Q.data[Q.r] = Q.data[Q.f]->rchild;
			Q.r++;
		}
		//然后打印（访问）队头元素,并将队头元素出队		
		printf("%c ", Q.data[Q.f]->data);
		Q.f++;//队头元素出队
	}
	printf("\n");
}

演示：

void main(){
	BiTree T;
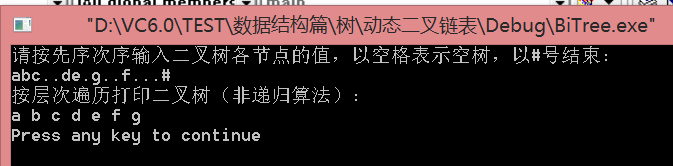
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	printf("按层次遍历打印二叉树（非递归算法）:\n");
	hierarchicalTraversePrint(T);
}

2.遍历二叉树的应用

2.1求二叉树的深度

//求二叉树的深度
int getBiTreeDepth(BiTree T){
	if(!T){
		return 0;
	}
	int leftTreeDepth = getBiTreeDepth(T->lchild);
	int rightTreeDepth = getBiTreeDepth(T->rchild);
	return leftTreeDepth > rightTreeDepth ? (leftTreeDepth+1) : (rightTreeDepth+1);
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	int depth = getBiTreeDepth(T);
	printf("该二叉树树的深度为%d\n", depth);
}

2.2求二叉树的结点数

//求二叉树的节点数
int getBiTreeSize(BiTree T){
	if(!T)
		return 0;
	int leftTreeSize = getBiTreeSize(T->lchild);
	int rightTreeSize = getBiTreeSize(T->rchild);
	return leftTreeSize + rightTreeSize + 1;
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	int size = getBiTreeSize(T);
	printf("该二叉树树的结点数为%d\n", size);
}

2.3求二叉树的叶子节点数

//先序遍历求叶子节点数
int getBiTreeLeafNodesNum2(BiTree T){
	if(T){
		if(!T->lchild && !T->rchild)
			return 1;
		else{
			int leftTreeLeafNodesNum = getBiTreeLeafNodesNum2(T->lchild);
			int rightTreeLeafNodesNum = getBiTreeLeafNodesNum2(T->rchild);
			return leftTreeLeafNodesNum + rightTreeLeafNodesNum;
		}
	}else{
		return 0;
	}
}

或者：

//先序遍历求叶子节点数
void getBiTreeLeafNodesNum(BiTree T, int &count){
	if(T){
		if(!T->lchild && !T->rchild)
			count++;
		//else{
			getBiTreeLeafNodesNum(T->lchild, count);
			getBiTreeLeafNodesNum(T->rchild, count);
		//}
	}
}

演示：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	int leafNodesNum2 = 0;
	leafNodesNum2 = getBiTreeLeafNodesNum2(T);
	printf("该二叉树树的叶子点数为%d\n", leafNodesNum2);
}

或者：

void main(){
	BiTree T;
	printf("请按先序次序输入二叉树各节点的值，以空格表示空树，以#号结束:\n");
	createBiTreeByPreOrder(T);

	int leafNodesNum = 0;
	getBiTreeLeafNodesNum(T, leafNodesNum);
	printf("该二叉树树的叶子点数为%d\n", leafNodesNum);
}