scikit-learn——Classification

Generalized Linear Models

线性回归（LinearRegression）

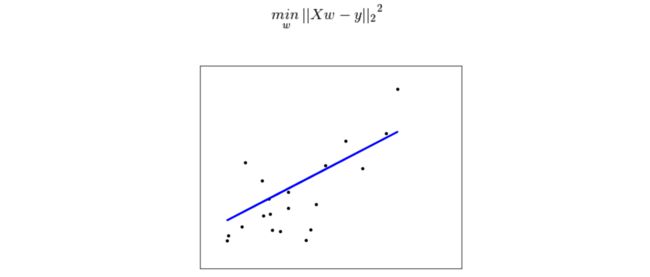
（Ordinary Least Squares）基于均方误差最小化来进行模型求解的方法称为最小二乘法。普通最小乘法线性回归就是最小化预测值与真实值的差的平方这个目标函数。

• 使用步骤：
  
  • 首先构建一个线性回归器clf
  • 然后让clf拟合数据集
  • coef_ 表示系数，intercept_表示截距

>>> from sklearn import linear_model
>>> clf = linear_model.LinearRegression()
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_
array([ 0.5,  0.5])
>>> clf.intercept_
1.11022302463e-16

• 参数解读：LinearRegression(fit_intercept=True, normalize=False,
  copy_X=True, n_jobs=1)括号里都是默认值。
  
  • fit_intercept：设置为False时，clf.intercept_==0.0，表示没有截距。
  • normalize：设置为True时，clf.coef_为[ 0.50000002 0.50000002]，输入的样本特征归一化。
  • copy_X：复制样本（True）或者重写样本（False）；
  • n_jobs ： If -1 all CPUs are used，加快速度，适用足够大的任务。

• 主要函数

  • fit(X, y[, sample_weight])：线性拟合样本数据。
  • predict(X) ：利用构建好的线性分类器进行预测。
  • score(X, y[, sample_weight])： 返回系数R^2 =(1 - u/v)，其中u= ((y_true - y_pred) ^ 2).sum() and v=((y_true - y_true.mean()) ^2).sum()

• 时间复杂度

  • 该方法利用奇异值分解求解这个平方最小化问题，如果矩阵的大小是(n, p) 那么时间复杂度是O(n p^2),假设n >= p.

岭回归（Ridge Regression）

岭回归其实就是在基本线性回归的基础上引入了正则化项L2范数，引入正则化有助于降低过拟合风险。

>>> from sklearn import linear_model
>>> clf = linear_model.Ridge (alpha = .5)
>>> clf.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1]) 
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)
>>> clf.coef_
array([ 0.34545455,  0.34545455])
>>> clf.intercept_ 
0.13636...

• 参数解读：Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=’auto’, random_state=None)[source]括号里都是默认值。

  • alpha ：alpha越大，表明先验的高斯协方差越小，模型越稳定， 相对的variance也越小。
  • max_iter ：共轭梯度求解的最大迭代次数。the default value is determined by scipy.sparse.linalg. For ‘sag’ solver, the default value is 1000.
  • solver ： {‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’}最后四个可以支持密集/稀疏数据。然而,只有sag’支持稀疏输入且fit_intercept = True.
  • tol : 问题的精度。
  • random_state ：{ int seed, RandomState instance, or None (default)}当采用’sag’(随机梯度下降法)时对数据进行洗牌时的伪随机数生成器的种子。

• 特殊Attributes：n_iter_ 表示每个样本迭代的次数，只有sag和 lsqr才有，其他的是None。

• 时间复杂度

  • 与基本线性回归相同。

RidgeCV

该方法就是内置了交叉验证的岭回归。

>>> from sklearn import linear_model
>>> clf = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])
>>> clf.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])       
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None,
    normalize=False)
>>> clf.alpha_                                      
0.1

• alpha ：Array of alpha values to try也就是alpha 这个参数不再是一个值，而是一个向量，里面的alpha 值分别进行回归，最终clf选择最优的alpha 。

套索回归（Lasso Regression）

套索回归和前面的岭回归类似，只不过套索回归采用的是L1范数。L1正则是laplace先验，L2是高斯先验，L1范数的一个好处是求得的解中w会有更少的非零分量（更稀疏的解）。

它倾向于用更少的参数来解决问题，如果预测的一组变量是高度相关的，Lasso 会选出其中一个变量并且将其它的收缩为零，通过这种方法有效的减少了参数。

>>> from sklearn import linear_model
>>> clf = linear_model.Lasso(alpha = 0.1)
>>> clf.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection='cyclic', tol=0.0001, warm_start=False)
>>> clf.predict([[1, 1]])
array([ 0.8])

• 参数解读：Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=’cyclic’)[source]括号里都是默认值。
  
  • precompute ：{True | False | ‘auto’ | array-like}利用预先计算格拉姆矩阵来加快计算速度。
• 时间复杂度
  
  • 该方法利用奇异值分解求解这个平方最小化问题，如果矩阵的大小是(n, p) 那么时间复杂度是O(n p^2),假设n >= p.