Stanford 机器学习-Neural Networks learning

1. Cost Function

字母含义：
nl 表示网络的层数
Ll 表示第l层
W(l)ij 表示第l层第j单元到第l+1层第i个单元之间的连接参数
b(l)i 表示是第l+1层第i单元的偏置项
a(l)i 表示是第l层第i单元的激活值（输出值）
z(l)i 第l层i单元输入加权和（包括偏置单元）
Sl 表示第l层的neuron个数。
- 二分类： Sl =1,y=0或者1
- 多分类问题 Sl =K, yi = 1表示分到第i类；（K>2）

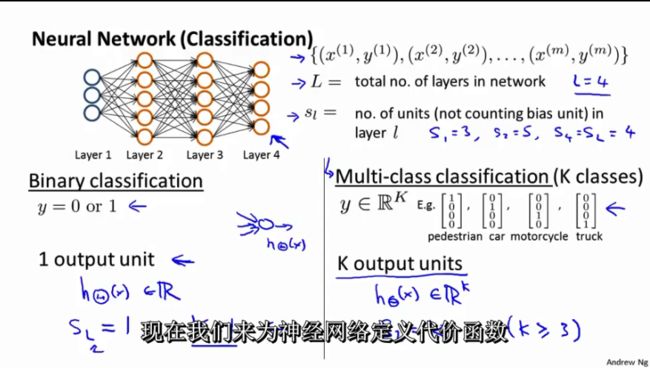
1.1两个cost function函数

其中前半部分是预测与真实值的距离，后半部分是用于正则化的bias项

∣w⃗ Tx⃗ +b∣∥w⃗ ∥ 任意点 x⃗  到超平面 (w⃗ ,b) 的距离。
公式 γ=2∥w⃗ ∥ 表示间隔
向量机的数学模型: min(w⃗ ,b⃗ )12∗∥w⃗ ∥2 ，使得 yi(w⃗ Tx⃗ i+b)≥1,i=1:m 。

2. Backpropagation Algorithm

我们的目的是最小化J(Θ)
下面公式中的第一项 J(W,b) 是一个均方差项。第二项是一个规则化项（也叫权重衰减项），其目的是减小权重的幅度，防止过度拟合。
权重衰减参数 λ 用于控制公式中两项的相对重要性。

通过forward propagation,首先算出training dataset 在神经网络上的各层输出值：
前向传播的公式:
z(l+1)=Wl⋅al+bl
a(l+1)=f(z(l+1))

根据 J(W,θ) 求偏导，可得出第 nl 层和第i层的 δ(l)j ， δ(l)j 表示实际值与网络产生的输出值的差异。
公式推导地址
对于第 nl 层：
δ(nl)i=−(yi−a(nl)i)⋅f′(z(nl)i)
对于第l层：
δ(l)i=(∑sl+1j=1Wjiδl+1j)f′(z(l)i)

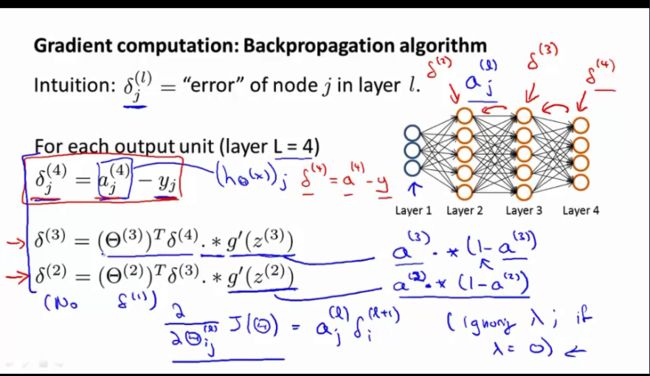
反向传播算法可以表示为以下几个步骤：
1. 进行前馈运算，求出所有层的激活值和加权和。
2. 对于输出层，计算 δ(nl)=−(y−a(nl))⋅f′(z(nl))
3. 对于其他层，计算 δ(l)=((W(l))Tδ(l+1))⋅f′(z(l))
4. 计算最终所需要的偏导数的值：
∇W(t)J(W,b;x,y)=δ(l+1)(a(l))T
∇b(t)J(W,b;x,y)=δ(l+1)
在梯度下降法一次迭代中:
1. 对于所有l，另 ΔW(l):=0 , Δb(l):=0
2. 对于i=1:m
使用反向传播算法计算 ∇W(t)J(W,b;x,y) 和 ∇b(t)J(W,b;x,y)
计算 ΔW(l):=ΔW(l)+∇W(t)J(W,b;x,y)
计算 Δb(l):=Δb(l)+∇b(t)J(W,b;x,y)
3. 更新权重参数
W(l)=W(l)−α[(1mΔW(l))+λW(l)]
b(l)=b(l)−α[1mΔb(l)]

3 Backpropagation Intuition

简述了BP算法
δ分量都等于后面一层所有的δ加权和，其中权值就是参数Θ。
θ(l)j=∑k=1θ(l)kj⋅θ(l+1)k

D作为cost function对参数的求导结果：
∂∂θ(l)ij=D(l)ij

4 unrolling parameters

首先将各层向量连接到一个vector里面传入function，然后展开，并进行计算。

5 gradient checking

主要就是通过gradient checking的方式，检查我们的BP算法是否正确。

6 Random Initialization

在初始化Theta值是，不能用0来初始化，而是随机初始化。

7 Putting It Together

简单叙述了如何选取隐层的数目和每层的节点数。

训练神经网络的步骤
1. 初始化权重
2. 对所有的 x(i) 进行forward propagation得到 hθ(x(i))
3. 实现cost function函数
4. 实现backprop 得到partial derivative
5. 用gradient checking来检验backprop算法是否正确，在训练前要disable
6. 通过梯度下降等算法最小化 J(θ)
梯度下降法不能保证得到全局最优解，但一般得到的结果都会比较好
对所有的training example进行训练