[机器学习] UFLDL笔记 - ICA（Independent Component Analysis）（Code）

引言

　机器学习栏目记录我在学习Machine Learning过程的一些心得笔记，涵盖线性回归、逻辑回归、Softmax回归、神经网络和SVM等等，主要学习资料来自Standford Ag老师的教程，同时也查阅并参考了大量网上的相关资料（在后面列出）。

　本文主要记录我在学习ICA（独立成分分析）过程中的心得笔记，对于ICA模型的理解和疑问，也纠正网络上一些Tutorial、资料和博文中的错误，欢迎大家一起讨论。
　全文共分为两个部分：
　ICA: Representation：ICA的模型描述；
　ICA: Code：ICA的代码实现。

前言

　本文主要介绍ICA的训练过程、代码以及实验结果（对应UFLDL的课后练习），源自于我在学习ICA过程中的笔记资料，包括了我个人对ICA模型的理解和代码实现，引用部分我都会标注出来，文章小节安排如下：
　1）实验基础
　2）实验结果
　3）实验代码
　4）参考资料
　5）结语

　关于ICA模型的基础知识可以参考：
　[机器学习] 笔记 - ICA（Independent Component Analysis）（Representation）
　

实验基础

　实验主要是基于UFLDL Tutorial中ICA部分的练习：Exercise:Independent Component Analysis，大家可以先参考该练习自己尝试完成实验。
　实验数据：STL-10 dataset

　ICA的目标函数：
　
　

　通过使用近似值“平滑” L1 范数，将ICA模型如下，
　标准正交ICA的目标函数：
　
　
　
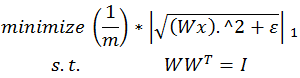
　标准正交ICA的目标函数对W的梯度：
　

注意事项：
（1）基底线性独立
　因为要学习到一组标准正交基，所以基向量的个数必须小于输入数据的维度。

（2）正交化
　注意一点，正交化通过来完成，其实现为：
　
　而不是
　

（3）白化
　对于标准正交ICA，样本数据必须经过无正则 ZCA 白化，即 ε 设为 0。

（4）均值化
　代价值和梯度必须除以样本数。

实验结果

（1）优化过程中采用Batch gradient descent，即梯度下降中利用全样本计算代价值及梯度
>>参数设置：
　alpha = 0.5，iteration = 50000，miniBatchSize = all

>>迭代输出：

 Iteration         Cost       time(s)
   1000        0.599483      62.35046
   2000        0.579602      158.1045
   3000        0.567833      222.5326
   4000        0.560265      287.4616
   5000        0.554130      349.7853
   ……………………………………………………
  16000        0.513359      1051.224
  17000        0.511163      1115.36
  18000        0.509213      1178.468
  19000        0.507456      1242.144
  20000        0.505815      1305.169
   ……………………………………………………
  36000        0.493431      2337.619
  37000        0.493253      2401.839
  38000        0.493097      2466.276
  39000        0.492961      2531.151
  40000        0.492841      2594.416
   ……………………………………………………
  46000        0.492322      2980.948
  47000        0.492257      3044.261
  48000        0.492197      3107.959
  49000        0.492144      3172.782
  50000        0.492096      3237.636

>>可视化：
迭代次数=10000

迭代次数=20000

迭代次数=30000

迭代次数=40000

迭代次数=50000

（2）优化过程中采用Mini-Batch Gradient Descent，即梯度下降中利用随机小批量样本计算代价值及梯度
>>参数设置：
　alpha = 0.5，iteration = 50000，miniBatchSize = 256

>>迭代输出：

 Iteration         Cost      time(s)
   1000        0.609892     4.643359
   2000        0.587216     9.270881
   3000        0.576038     13.96519
   4000        0.550711     18.70056
   5000        0.559629      23.6164
   ……………………………………………………
  16000        0.454444     79.16564
  17000        0.492942     84.36821
  18000        0.491434     89.44777
  19000        0.467292      94.3471
  20000        0.496667     99.20195
   ……………………………………………………
  26000        0.481736     138.9745
  27000        0.508776      144.397
  28000        0.462674     149.7803
  29000        0.524727     155.0663
  30000        0.480356      160.018
   ……………………………………………………
  36000        0.500814     190.5871
  37000        0.470674     195.8069
  38000        0.481720     200.8657
  39000        0.501621      205.682
  40000        0.536511     210.5624
   ……………………………………………………
  46000        0.478799      240.977
  47000        0.487278     246.0048
  48000        0.465347     250.7841
  49000        0.493228       255.54
  50000        0.495050     260.2548

>>可视化：
迭代次数=50000

>>分析
　采用 Mini-Batch Gradient Descent 可以在保证训练效果的同时，显著加快训练速度。
　采用Batch Gradient Descent和Mini-Batch Gradient Descent的最终效果对比如下：

　

（3）优化过程中采用Mini-Batch Gradient Descent，并设置 alpha = 16.0
>>参数设置：
　alpha = 16，iteration = 10000，miniBatchSize = 256
>>迭代输出：

 Iteration         Cost       time(s)
   1000        0.512445       4.92836
   2000        0.519963      9.913733
   3000        0.508143       14.9235
   4000        0.499603      19.89993
   5000        0.488427      24.81049
   6000        0.520706      29.91749
   7000        0.489411      34.86197
   8000        0.503602      39.87117
   9000        0.507514      44.86402
  10000        0.494073      49.80321

>>可视化：
迭代次数=10000

>>分析
　可以发现，随着 alpha 的增大，收敛速度越快，当alpha=16.0，基本上迭代10000次就可以达到不错的效果。但另一方面，cost下降的就没有那么稳定了。

实验代码

　在UFLDL - Exercise:Independent Component Analysis 基础上，我分别实现了Batch Gradient Descent和Mini-Batch Gradient Descent，并对参数 alpha 进行调整以实验不同参数下的训练情况。
　需要重点说明的是，
　第一，我在ICA优化过程中去除了线性搜索部分（代码中的while 1循环），因为我觉得这段线性搜索代码有些问题，因此非常容易陷入死循环。如果有朋友能理解这部分代码实现，务必请留言交流。
　第二，在orthonormalICACost函数中添加了一个miniBatchSize参数，用于实现Mini-Batch Gradient Descent。

　关于参数设置，
　迭代次数 iteration 和 学习率 alpha 的设置对训练速度和效果有直接的影响，对于本文中实现的ICA算法，实验了下面几种设置，
　1）alpha = 0.5，iteration = 10000, 20000, 50000
　2）alpha = 1.0，iteration = 10000, 20000, 50000
　3）alpha = 2.0，iteration = 10000, 20000, 50000
　4）alpha = 4.0，iteration = 10000, 20000, 50000
　5）alpha = 16.0，iteration = 10000, 20000, 50000
　可以发现随着 alpha 的增大，收敛速度越快，基本上 （alpha = 16.0，iteration = 10000） 就可以达到 （alpha = 0.5，iteration = 50000） 的效果。

　以下给出代码关键部分的实现：
　
　ICAExercise.m

%% CS294A/CS294W Independent Component Analysis (ICA) Exercise

%% STEP 0: Initialization
numPatches = 20000;
numFeatures = 121;
imageChannels = 3;
patchDim = 8;
visibleSize = patchDim * patchDim * imageChannels;
miniBatchSize = 256;
% 说明：
% 如果采用Batch Gradient Descent，则另 miniBatchSize = numPatches 
% 如果采用Mini-Batch Gradient Descent，则另 miniBatchSize = 随机采样值，例如 256。

%% STEP 1: Sample patches
%% STEP 2: ZCA whiten patches
%% STEP 3: ICA cost functions
% 说明：
% 这部分是 ICA cost function测试，测试通过后注释掉。

%% STEP 4: Optimization for orthonormal ICA

% 随机初始化W
weightMatrix = rand(numFeatures, visibleSize);

fprintf('%11s%16s%10s%12s\n','Iteration','Cost','t','time');

startTime = tic();

% Initialize some parameters for the backtracking line search
% 初始化参数设置
alpha = 0.5;            % 0.5, 16.0
t = 0.02;                  
lastCost = 1e40;

% 梯度下降

[cost, grad] = orthonormalICACost(weightMatrix(:), visibleSize, numFeatures, patches, epsilon, miniBatchSize);

% Do 10000 iterations of gradient descent
for iteration = 1:50000

    grad = reshape(grad, size(weightMatrix));
    newCost = Inf;        
    linearDelta = sum(sum(grad .* grad));

    % ===> 直接计算，去除线性搜索
    % 梯度下降
    considerWeightMatrix = weightMatrix - alpha * grad;
    % 正交化
    considerWeightMatrix = (considerWeightMatrix * considerWeightMatrix') ^ (-0.5) * considerWeightMatrix;
    [newCost, newGrad] = orthonormalICACost(considerWeightMatrix(:), visibleSize, numFeatures, patches, epsilon, miniBatchSize);
    % 更新参数矩阵（基底）
    weightMatrix = considerWeightMatrix;    

    % ===> 线性搜索，确定最优的alpha。这段代码似乎有点问题，这里注释掉了。
    %{
    % Perform the backtracking line search
    while 1
        considerWeightMatrix = weightMatrix - alpha * grad;
        % -------------------- YOUR CODE HERE --------------------
        % Instructions:
        % Write code to project considerWeightMatrix back into the space
        % of matrices satisfying WW^T = I.
        % 
        % Once that is done, verify that your projection is correct by 
        % using the checking code below. After you have verified your
        % code, comment out the checking code before running the
        % optimization.

        % Project considerWeightMatrix such that it satisfies WW^T = I
        %error('Fill in the code for the projection here'); 

        % 正交化
        considerWeightMatrix = (considerWeightMatrix * considerWeightMatrix') ^ (-0.5) * considerWeightMatrix;

        %{
        % 正交化计算结果验证，完成后注释掉
        % Verify that the projection is correct
        temp = considerWeightMatrix * considerWeightMatrix';
        temp = temp - eye(numFeatures);
        assert(sum(temp(:).^2) < 1e-23, 'considerWeightMatrix does not satisfy WW^T = I. Check your projection again');
        %error('Projection seems okay. Comment out verification code before running optimization.');
        %}
        % -------------------- YOUR CODE HERE -------------------- 

        [newCost, newGrad] = orthonormalICACost(considerWeightMatrix(:), visibleSize, numFeatures, patches, epsilon, miniBatchSize);

        if newCost > lastCost - alpha * t * linearDelta
            t = 0.9 * t;
        else
            break;
        end
    end

    lastCost = newCost;
    weightMatrix = considerWeightMatrix;

    t = 1.1 * t;

    %}


    cost = newCost;
    grad = newGrad;

    % Visualize the learned bases as we go along 
    if mod(iteration, 1000) == 0
        duration = toc(startTime);
        fprintf(' %9d %14.6f %8.7g %10.7g\n', iteration, newCost, t, duration);
        % Visualize the learned bases over time in different figures so 
        % we can get a feel for the slow rate of convergence
        figure(floor(iteration /  1000));
        displayColorNetwork(weightMatrix'); 
    end

end

% 可视化
% Visualize the learned bases
displayColorNetwork(weightMatrix');

　
　orthonormalICACost.m

function [cost, grad] = orthonormalICACost(theta, visibleSize, numFeatures, patches, epsilon, miniBatchSize)
%orthonormalICACost - compute the cost and gradients for orthonormal ICA
% (i.e. compute the cost ||Wx||_1 and its gradient)

    weightMatrix = reshape(theta, numFeatures, visibleSize);

    cost = 0;
    grad = zeros(numFeatures, visibleSize);

    % -------------------- YOUR CODE HERE --------------------
    % Instructions:
    % Write code to compute the cost and gradient with respect to the
    % weights given in weightMatrix. 
    % -------------------- YOUR CODE HERE -------------------- 

    % Random sampling
    patches_rndIdx = randperm(size(patches, 2));
    patches = patches(:, patches_rndIdx(1:miniBatchSize));
    numExamples = miniBatchSize;

    % Compute cost value
    L1Matrix = sqrt((weightMatrix * patches).^2 + epsilon);
    cost = sum(sum(L1Matrix)) / numExamples;

    % Compute gradient
    grad = weightMatrix * patches ./ L1Matrix * patches';
    grad = grad(:) ./ numExamples;

end

　

参考资料

UFLDL Tutorial (new version)
http://ufldl.stanford.edu/tutorial/
UFLDL Tutorial (old version)
http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial
Exercise:Independent Component Analysis
http://ufldl.stanford.edu/wiki/index.php/Exercise:Independent_Component_Analysis
Deep learning：三十九(ICA模型练习)
http://www.cnblogs.com/tornadomeet/archive/2013/05/07/3065953.html

结语

　以上就是ICA模型的训练过程，包括实验代码以及实验结果，至此完成对ICA算法的初步学习，也将笔记资料写在这里与大家交流，谢谢！

　本文的文字、公式和图形都是笔者根据所学所看的资料经过思考后认真整理和撰写编制的，如有朋友转载，希望可以注明出处：　
　[机器学习] UFLDL笔记 - ICA（Independent Component Analysis）（Code）
　http://blog.csdn.net/walilk/article/details/50471658

·