各种排序的排序思想和实现

     今天主要和大家讨论八大排序算法，包括冒泡排序、插入排序、选择排序、shell排序、归并排序、快速排序、计数排序、堆排序。通过和大家的讨论，相信对大家的在今后的学习和面试肯定会有很大的帮助。下面分别来说明各种排序的排序的思想和其实现。

      （1）冒泡排序：

             排序思想：设数组a[0..n-1]，令i = 0，j从1到n - i 判断相邻的元素的大小，如果a[j - 1] > a[j]，交换a[j - 1]、a[j]，则对于一趟排序来说，就可以将数组的最大值冒泡的a[n - 1]的位置；

  下面给出冒泡排序的程序：

void bubble_sort(int *array,int length)
{
    int i = 0;
    int j = 0;
    int temp = 0;
    for(i = 0;i < length;++i){
        for(j = 1;j < length - i;++j){
            if(array[j - 1] > array[j]){
                temp = array[j - 1];
                array[j - 1] = array[j];
                array[j] = temp;
            }
        }
    }
}

在此应注意的是，i和j遍历数组的范围，因为每次冒泡都会使得最大的元素位于数组的最后，则下一次排序时，位于数组的后面的元素不用参与排序，所以j是从1到length - i。

对于冒泡排序还可以进行优化，其优化的代码如下：

void bubble_sort1(int *array,int length)
{
    Boolean flag = TRUE;
    int j = 0;
    int temp = 0;
    while(flag){
        flag = FALSE;
        for(j = 1; j < length;++j){
            if(array[j - 1] > array[j]){
                temp = array[j - 1];
                array[j - 1] = array[j];
                array[j] = temp;
                flag = TRUE;
            }
        }
        length--;
    }
}

当出现在其中一次中没有发生交换，则说明数组的元素已经升序，则排序完成。

由此可看出冒泡排序的时间复杂度为o(n^2)，并且是一种发生在相邻元素的交换，所以冒泡排序是一种稳定的排序。

    （2）插入排序：

            排序思想：设数组a[0..n-1]，

            1> 初始时，a[0]自成一个有序序列，无序区为a[1..n-1] ，令i = 1；

            2>将a[i]插入到当前有序区a[0..i - 1]形成有序区a[0..i];

           3>i++重复第二步骤，使得i == n - 1，排序结束。

下面给出插入排序的代码实现：

void insert_sort(int *array,int length)
{
    int i = 0;
    int j = 0;
    int temp = 0;
    for(i = 1;i < length;++i){
        temp = array[i];
        for(j = i - 1;j >= 0 && array[j] > temp;j--){
            array[j + 1] = array[j];
        }
        array[j + 1] = temp;
    }
}

  由此可见看出插入排序的时间复杂度为o(n^2)，插入排序并不是相邻元素交换，所以插入排序是不稳定的。

       （3）选择排序：

              排序思想：设数组a[0..n-1]；
                1> 初始时，数组全为无序区为a[0..n-1].令i = 0
                2>在无序区a[i..n-1]中选取一个最小的元素，将其与a[i]交换，交换之后a[0    ..i] ， 就形成了一个有序区。
                3> i++并重复第二步直到i==n-1,排序完成。

选择排序的代码实现：

void select_sort(int *array,int length)
{
    int i = 0;
    int j = 0;
    int min_index = -1;
    int temp = 0;
    for(i = 0;i < length;++i){
        min_index = i;
        for(j = i + 1;j < length;++j){
            if(array[j] < array[min_index]){
                min_index = j;
            }
        }
        if(min_index != i){
            temp = array[min_index];
            array[min_index] = array[i];
            array[i] = temp;
        }
    }
}

选择排序的时间复杂度仍为o(n^2),并且是一种不稳定的排序。
对于这三种排序的结果如下：

  在数据规模比较小的时候，这三种排序消耗的时间都比较短；当我们把数据规模扩大到1万的时候，其消耗的时间如下：

                    

由程序的执行效果来说，在数据规模在1万左右时，插入排序的效率是三种排序中执行效率最快的，最慢的是冒泡排序。

接下来我们讨论的排序都比上述的排序效率高，首先我们来看shell排序，

         （4）shell排序：设数组a[0 .. n-1]

                 排序思想：shell排序可以说是插入排序的升级版，其中gap称为增量，在本程序中gap是从n / 2，减到1

，每次进行插入排序，当gap 减为1时，就和上述的插入排序一样。

          shell排序的代码实现：

void shell_sort(int *array,int length)
{
    int gap = 0;
    int i = 0;
    int j = 0;
    int temp = 0;
    for(gap = length / 2;gap > 0;gap /= 2){
        for(i = gap;i < length;++i){
            temp = array[i];
            for(j = i - gap;j >= 0 && array[j] > temp;j -= gap){
                array[j + gap] = array[j];
            }
            array[j + gap] = temp;
        }
    }    
}

shell排序也被称为缩小增量排序，是不稳定的排序。

       （5）归并排序：

          排序思想：其主要用到分治的思想，假设数组为a[ 8 ] = {3,2,5,9,0,7,4,6}，归并排序首先堆数组进行拆分，直到每个元素单独看成一个数组，然后进行合并，上述数组拆分到最后为 ：

3       2         5         9           0          7        4        6；

第一次合并的结果为：2  3  5  9  0  7  4  6

第二次合并的结果为：2  3  5  9  0  4  7  6

第三次合并的结果为：0  2  3  4  5  6  7  9

其代码实现如下：

static void merge_array(int *array,int left,int mid,int right,int *temp)
{
    int i = left;
    int j = mid + 1;
    int m = mid;
    int n = right;
    int k = 0;
    while(i <= m && j<= n){
        if(array[i] <= array[j]){
            temp[k++] = array[i++];
        }else{
            temp[k++] = array[j++];
        }
    }
    while(i <= m){
        temp[k++] = array[i++];
    }
    while(j <= n){
        temp[k++] = array[j++];
    }
    memcpy(array + left, temp,sizeof(int) * k);
}
static void Merge_sort(int *array,int left,int right,int *temp)
{
    int mid = -1;
    if(left < right){
        mid = (left + right) / 2;
        //拆分
        Merge_sort(array,left,mid,temp);
        Merge_sort(array,mid + 1,right,temp);
        //合并
        merge_array(array,left,mid,right,temp);
    }
}
void merge_sort(int *array,int length)
{
    int *temp = NULL;
    
    if(array == NULL || length < 2){
        return ;
    }
    temp = (int *)Malloc(sizeof(int) * length);
    Merge_sort(array,0,length - 1,temp);
    free(temp);
}

merge_array函数为合并过程，Merge_sort函数为拆分过程。

归并排序的时间复杂度为o(n * log 2^n)，归并排序为稳定的排序。

     （6）快速排序：

           排序思想：和归并排序的思想一样，用到分治的思想，

假设数组a[10] = { 12 , 3,  45 , 65 , 18 , 5 , 2 , 11 , 4}

第一次快排的具体情况如下：

         value = 12

把比12大的放在右边，比12的放在左边

12   3    45    65    18   5    2    11    4

i                                                        j              a[ j ]  < value

4    3    45    65    18    5    2    11    4

      i                                                  j               a[i]  < value 则 i++

4    3    45    65    18    5    2    11    4

             i                                           j               a[ i ]  >value 则 a[ j ] = a[ i ]

4    3    45    65    18    5    2    11    45

             i                                    j                       a[  j ]   <value 则 a[  i ] = a[ j ]

4    3    11    65    18    5    2    11    45

                     i                            j                       a[ i ]  >value 则 a[ j ] = a[ i ]

4    3    11    65    18    5    2    65    45

                     i                     j                               a[  j ]   <value 则 a[  i ] = a[ j ]

4    3    11    2    18      5    2    65    45

                            i              j                                a[ i ]  >value 则 a[ j ] = a[ i ]

4    3     11    2    18     5    18    65    45

                             i       j                                      a[  j ]   <value 则 a[  i ] = a[ j ]

4    3    11      2    5     5     18    65    45

                                    ij                                       a[  i  ] = value

4    3    11    2      5      12    18    65    45

接下来则分别左递归，右递归。

快排的代码实现如下：

void quick_sort(int *array,int left,int right)
{
    int i = left;
    int j = right;
    int value = array[left];
    if(left < right){
        while(i < j){
            for(;j > i && array[j] > value;j--);
            if(j > i){
                array[i++] = array[j];
            }
            for(;i < j && array[i] < value;++i);
            if(i < j){
                array[j--] = array[i];
            }
        }
        array[i] = value;
        quick_sort(array,left,i - 1);
        quick_sort(array,i + 1,right);
    }
}

还有一种实现如下：

static int partition(int *array,int left,int right)
{
    int i = left - 1;
    int j = 0;
    int value = array[right];
    int temp = 0;
    for(j = left;j <= right - 1;++j){
        if(array[j] < value){
            i = i + 1;
            temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    temp = array[i + 1];
    array[i + 1] = array[right];
    array[right] = temp;
    return i + 1;
    
}
void quick_sort1(int *array,int left,int right)
{
    int q = 0;
    if(left < right){
        q = partition(array,left,right);
        quick_sort1(array,left,q - 1);
        quick_sort1(array,q + 1,right);
    }
}

快排是一种不稳定的排序，其时间复杂度为o(n * log 2^n)，对于有一定的顺序的序列，其快排的效率会明显下降。

接下来我们来看shell、归并和快排的执行结果：

对于1亿个数据的，以上的三种排序消耗的时间如下：

      （7）计数排序：

          排序思想：计数排序可以看成是hash的一种应用，适合数据比较集中的序列，首先统计数组中元素出现的次数，然后在将其合并。

代码的实现如下：

void count_sort(int *array,int length,int min,int max)
{
    int *count = NULL;
    int c_size = max - min + 1;
    int i = 0;
    int j = 0;
    count = (int *)Malloc(sizeof(int) * c_size);
    bzero(count,sizeof(int) * c_size);
    for(i = 0; i < length;++i){
        count[array[i] - min]++;
    }
    for(i = 0,j = 0; i < c_size;){
        if(count[i]){
            array[j++] = i + min;
            count[i]--;
        }else{
            i++;
        }
    }
    free(count);
}

时间复杂度为o(n).

     (8)堆排序：

        堆排序思想：在之前的博客中也详细介绍了堆排序，大家可以进行参考，今天则不过多说明，主要将堆排序和其他几种排序进行比较；

    代码的实现：

void heap_sort(int *array,int length)
{
    int i = 0;
    int temp = 0;
    int n = length;
    build_max_heap(array,length);
    for(i = length;i >= 1;i--){
        temp = array[0];
        array[0] = array[i -1];
        array[i - 1] = temp;
        n--;
        Max_heapify(array,1,n);
    }
}
static int Left(int i)
{
    return 2 * i;
}
static int Right(int i)
{
    return 2 * i + 1;
}
static int Parent(int i)
{
    return i / 2;
}
static void Max_heapify(int *array,int i ,int length)
{
    int left = Left(i);
    int right = Right(i);
    int largest = 0;
    int temp = 0;
    if(left <= length && array[left - 1] > array[i - 1]){
        largest = left;
    }else{
        largest = i;
    }
    if(right <= length && array[right - 1] > array[largest - 1]){
        largest = right;
    } 
    if(largest != i){
        temp = array[i - 1];
        array[i - 1] = array[largest -1];
        array[largest - 1] = temp;
        Max_heapify(array,largest,length);
    }
}
void build_max_heap(int *array,int length)
{
    int i = 0;
    for(i = length / 2;i >= 1; i--){
        Max_heapify(array,i,length);
    }

 
}

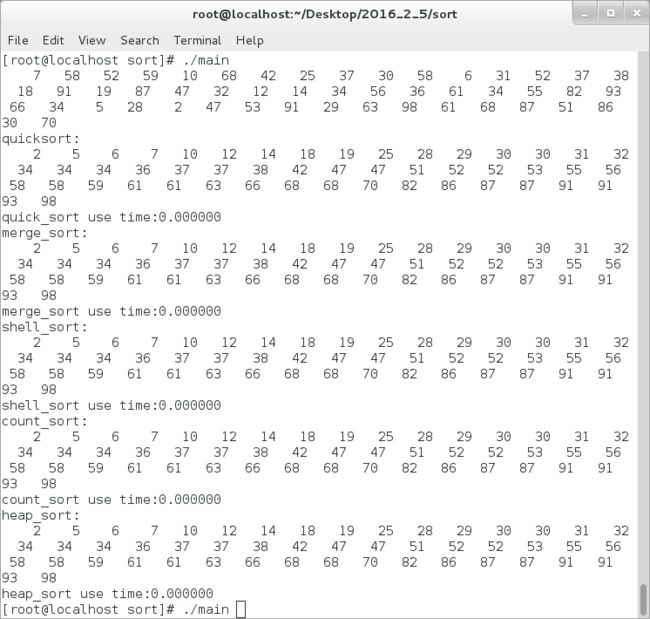
对于以上的几种排序，其执行结果如下图：

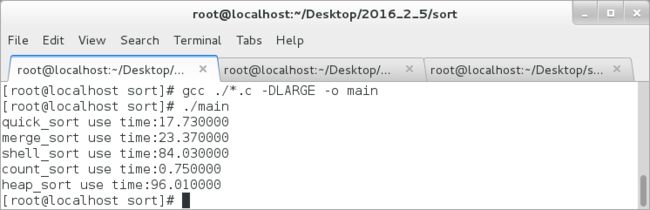
接下来再来看其对时间的消耗：

   

由此看来，对于1亿的数据进行排序，计数排序的效率更高，计数排序适用于数据比较集中的序列，其次是快排，最慢的则是堆排。

接下来我们对于10亿个数据再进行测试：

由图得出还是计数排序的效率更高一些。

下面给出主程序的代码：

int main(int argc,char** argv)
{
    clock_t start = 0;
    clock_t end = 0;
    double use_time = 0;
    int *array1 = NULL;
    int *array2 = NULL;
    int *array3 = NULL;
    int *array4 = NULL; 
    int *array5 = NULL;
    int *array6 = NULL; 
    array1 = (int *)Malloc(sizeof(int) * SIZE);
    radom_array(array1,SIZE); 
    array2 = (int *)Malloc(sizeof(int) * SIZE);
    memcpy(array2,array1,sizeof(int) *SIZE);
    array3 = (int *)Malloc(sizeof(int) * SIZE);
    memcpy(array3,array1,sizeof(int) *SIZE);
    array4 = (int *)Malloc(sizeof(int) * SIZE);
    memcpy(array4,array1,sizeof(int) *SIZE);
    array5 = (int *)Malloc(sizeof(int) * SIZE);
    memcpy(array5,array1,sizeof(int) *SIZE);
    array6 = (int *)Malloc(sizeof(int) * SIZE);
    memcpy(array6,array1,sizeof(int) *SIZE);
    //序列1：
    #ifdef PRINT
    print_array(array1,SIZE);
    start = clock();
    //bubble_sort(array1,SIZE);
    quick_sort(array1,0,SIZE - 1);
    end = clock();
    printf("quicksort:\n");
    print_array(array1,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("quick_sort use time:%lf\n",use_time);

    #else
    start = clock();
    quick_sort(array1,0,SIZE - 1);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("quick_sort use time:%lf\n",use_time);
    #endif
    //序列2：
    #ifdef PRINT
    start = clock();
    //bubble_sort1(array2,SIZE);
    //insert_sort(array2,SIZE);
    merge_sort(array2,SIZE);
    end = clock();
    printf("merge_sort:\n");
    print_array(array2,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("merge_sort use time:%lf\n",use_time);

    #else
    start = clock();
    //bubble_sort(array2,SIZE);
    //insert_sort(array2,SIZE);
    merge_sort(array2,SIZE);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("merge_sort use time:%lf\n",use_time);
    #endif
    //序列3：
    #ifdef PRINT
    start = clock();
    //quick_sort1(array3,0,SIZE - 1);
    shell_sort(array3,SIZE);
    end = clock();
    printf("shell_sort:\n");
    print_array(array3,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("shell_sort use time:%lf\n",use_time);

    #else
    start = clock();
    //quick_sort1(array3,0,SIZE - 1);
    shell_sort(array3,SIZE);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("shell_sort use time:%lf\n",use_time);
    #endif
    //序列4：
    #ifdef PRINT
    start = clock();
    count_sort(array4,SIZE,0,MODE_SIZE);
    end = clock();
    printf("count_sort:\n");
    print_array(array4,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("count_sort use time:%lf\n",use_time);

    #else
    start = clock();
    count_sort(array4,SIZE,0,MODE_SIZE);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("count_sort use time:%lf\n",use_time);
    #endif
    #if 0
    //序列5：
    #ifdef PRINT
    start = clock();
    base_sort(array5,SIZE,0,MODE_SIZE);
    end = clock();
    printf("base_sort:\n");
    print_array(array5,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("base_sort use time:%lf\n",use_time);

    #else
    start = clock();
    base_sort(array5,SIZE,0,MODE_SIZE);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("base_sort use time:%lf\n",use_time);
    #endif
    #endif
    //序列6：
    #ifdef PRINT
    start = clock();
    heap_sort(array6,SIZE);
    end = clock();
    printf("heap_sort:\n");
    print_array(array6,SIZE);

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("heap_sort use time:%lf\n",use_time);

    #else
    start = clock();
    heap_sort(array6,SIZE);
    end = clock();

    use_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("heap_sort use time:%lf\n",use_time);
    #endif
    return 0;
}

    还有一个排序为基数排序，将在下次的博客中和大家分享！！！