后缀数组学习笔记
学习算法...
准备工作中...
一直耳闻后缀数组的神奇,据说是解答字符串类型题目的神器...故作此文,权作学习笔记...
何谓后缀数组?下面介绍几个名词的基本定义:
子串:令字符串S [0..n],则子串s[i..j](0<= i <= j <=n)表示字符串S中从位置 i 到位置 j 顺次排列的一段字符列;
后缀:后缀是指从位置 i 开始到整个串尾结束的一个子串,如后缀Suffix(i) = s[i..n];
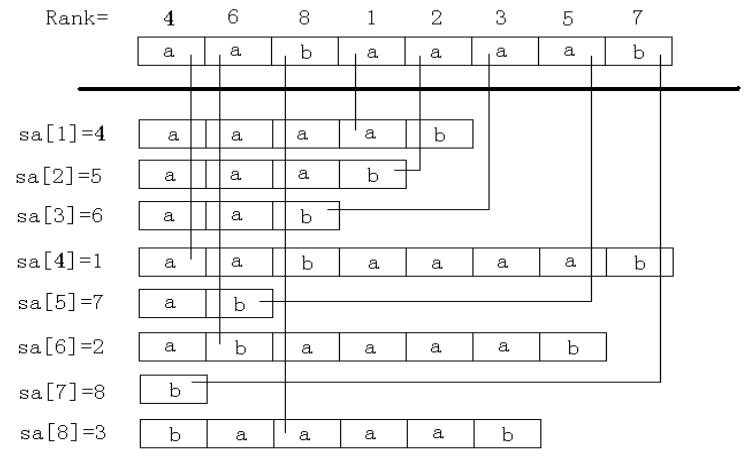
后缀数组:后缀数组SA[0..n]是一个一维数组,数组中保存的值满足这样的一个关系:Suffix(SA[0]) < Suffix(SA[1]) < ... < Suffix(SA[n]), 字符串比较遵照C语言的compare函数比较规则;
名次数组:名次数组Rank[0..n]保存的是后缀Suffix(i)在所有(n+1)个后缀数组中排列的名次。
容易推出后缀数组和名次数组满足这样的一个关系: Rank[SA[i]] = i, 如图所示:
由此,我们知道后缀数组和名次数组是互逆运算,知道其中一个,在O(n)的时间范围内可以求出另一个...
ok... 主要的基本名词定义介绍完毕... 现在介绍一种简单的构造给定字符串后缀数组的方法...俗称倍增算法...看完该算法,自然会明白为何会起名倍增啦~
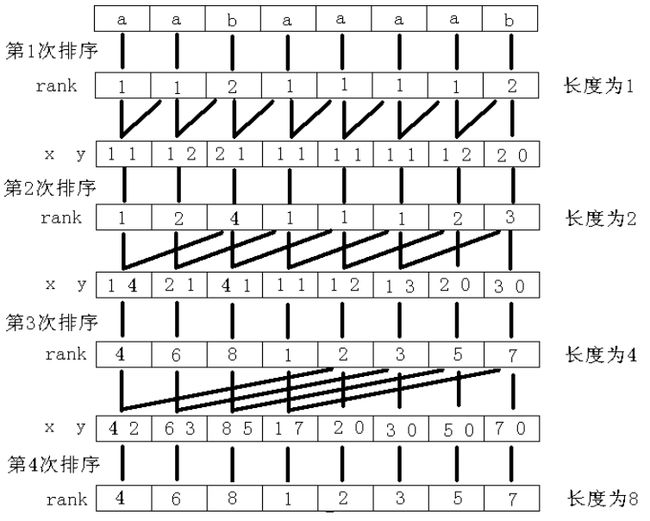
倍增算法的思路:用倍增的方法对以每个字符开始的长度为2^k的子字符串进行排序,求出排名。k从0开始,每次加1,当2^k大于n时,则停止迭代,此时相当于求出了所有后缀子串的排名?!
是的,你没看错...倍增算法的思路就是这么简单...看完这句话你肯定会有这些疑问:
1.如何对子字符串排序?
2.当子串的长度不是2的整数次幂时,如何处理?
3.如何迭代?前面介绍的名次数组和后缀数组在迭代过程中有什么作用?
在解答这些疑问时,我们先简单熟悉下基数排序:
基数排序也称关键字排序,是一种稳定的排序算法,稳定这一性质在实现后缀数组很重要...因为在倍增算法中用到的基数排序中使用了两个关键字,所以我们也以两个关键字的基数排序举例:
假设要对以下数据进行排序:73 22 93 43 55 14 28 65 39 81
第一步:首先遍历数据,根据每个数据的个位数(第二关键字),按照遍历的顺序依次放进编号0~9的桶,个位数值与桶编号一一对应,分配结果如下所示:
按照桶编号从小到大,桶内按照放入顺序(也是遍历顺序,类似队列)把所有数据重新串起来:81 22 73 93 43 14 55 65 28 39这就是按照第二关键字(个位数值)排列得到的结果;
第二步:依次遍历上述得到的数据序列,按照十位数值(第一关键字)重复上述操作,结果如下:
按照同样的规则,取出这些 数据:14 22 28 39 43 55 65 73 81 93,这样原数据排序完毕...
ok...现在我们尝试解答上面提出的三个问题...
1.如何对子字符串排序?
除k=0外,每次排序都利用上次长度为2^(k-1)的子字符串的rank值,那么长度为2^k的子字符串就可以用两个长度为2^(k-1)的子字符串的rank值作为关键字表示,然后根据关键字基数排序;
2.当子串的长度不是2的整数次幂时,如何处理?
若该子字符串长度小于或等于2^(k-1)时,那么它的第二关键字默认最小(字符串比较的性质决定, ),第一关键字按照上次迭代求出的改子字符串rank值表示;若该子字符串长度小于2^k时,第一关键字和第二关键字依然是按照上次迭代求出的相应子字符串rank值表示;
3.如何迭代?前面介绍的名次数组和后缀数组在迭代过程中有什么作用?
迭代的终止条件是rank的值都不相同,此时所有的后缀字符串rank值都求出来,也只有在此时后缀数组和名次数组才满足互逆预算规则,因为所有的rank值都不同。每次迭代求后缀数组和名次数组都用到了上次迭代的名次数组来获取关键字大小。
为了更直观的查看倍增算法的过程分析(x,y分别表示第一、二关键字),参考下图:
ok...接下来我们研究下代码,先贴出后缀数组的整个实现代码:
// SuffixArray.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <vector>
#include <iostream>
#include <string>
#define maxn 1000
using namespace std;
int X[maxn] = { 0 }, Y[maxn] = { 0 }, Sa[maxn] = { 0 }, Wr[maxn] = { 0 };
bool my_cmp(int *x, int a, int b, int l){
return x[a] == x[b] && x[a + l] == x[b + l];
}
void my_getSa(int len, int up){
int i, j, p;
//k = 0, 初始化名次数组X和后缀数组Sa;需要指出的是,这里偷懒没有求出每个后缀的真正名次,而是代以字符值,但本质是一样的
for (i = 0; i < up; ++i) Wr[i] = 0;
for (i = 0; i < len; ++i) Wr[X[i]] += 1;
for (i = 1; i < up; ++i) Wr[i] += Wr[i - 1];
for (i = len - 1; i >= 0; --i) Sa[--Wr[X[i]]] = i;
//求k>0的情况,依次迭代,知道名次数组中没有相同的rank值
for (p = 1, j = 1; p < len; j *= 2, up = p){
//第一步,下面两个循环,用数组Y存储根据第二关键字排序后的序列
for (p = 0, i = len - j; i < len; ++i) Y[p++] = i;
for (i = 0; i < len; ++i) if (Sa[i] >= j) Y[p++] = Sa[i] - j;
//第二步,根据第一关键字对得到的序列Y进行排序
for (i = 0; i < up; ++i) Wr[i] = 0;
for (i = 0; i < len; ++i) Wr[X[Y[i]]] += 1;
for (i = 1; i < up; ++i) Wr[i] += Wr[i - 1];
//后缀数组
for (i = len - 1; i >= 0; --i) Sa[--Wr[X[Y[i]]]] = Y[i];
//名次数组
for (i = 1, Y[Sa[0]] = 0, p = 1; i < len; ++i) Y[Sa[i]] = my_cmp(X, Sa[i - 1], Sa[i], j) ? p - 1 : p++;
//复制名次数组Y到X
for (i = 0; i < len; ++i) X[i] = Y[i];
}
}
int _tmain(int argc, _TCHAR* argv[])
{
string str;
cin >> str;
int len = str.size();
for (int i = 0; i < len; ++i) X[i] = (int)str[i];
my_getSa(len, int('z') + 1);
for (int i = 0; i < len; ++i) cout << Sa[i] << '\t'; cout << endl;
for (int i = 0; i < len; ++i) cout << X[i] << '\t'; cout << endl;
return 0;
}
下面我们逐步分析代码:
数组X存储名次数组(初始化时,直接赋以字符数值--在main函数中),数组Sa存储后缀数值,下面是初始化代码:
for (i = 0; i < up; ++i) Wr[i] = 0; for (i = 0; i < len; ++i) Wr[X[i]] += 1; for (i = 1; i < up; ++i) Wr[i] += Wr[i - 1]; for (i = len - 1; i >= 0; --i) Sa[--Wr[X[i]]] = i;
这里需要注意的是第四个for循环中,i是从大到小遍历的,因为在进行基数排序的时候,如果两个数相等,那么遍历越在前名次值越高,参考上面基数排序;
在进行第k+1次迭代时,我们要进行两个关键字的排序,第一步是对第二关键字进行排序,实际上,第二关键字排序的结果已经存储在上次求得Sa中:
for (p = 0, i = len - j; i < len; ++i) Y[p++] = i; for (i = 0; i < len; ++i) if (Sa[i] >= j) Y[p++] = Sa[i] - j;第一个循环的意思是:以i开始的字符串没有第二关键字,直接默认他的第二关键字最小,放入数组Y中
第二步是对第一关键字排序,遍历数组Y,类似于初始化的方法计算后缀数组:
for (i = 0; i < up; ++i) Wr[i] = 0; for (i = 0; i < len; ++i) Wr[X[Y[i]]] += 1; for (i = 1; i < up; ++i) Wr[i] += Wr[i - 1]; for (i = len - 1; i >= 0; --i) Sa[--Wr[X[Y[i]]]] = Y[i];
第三步是利用后缀数组求名次数组,因为Y已经不需要了,所以暂存在Y中,然后把结果从Y复制到数组X中,用以下一次迭代
<span style="white-space:pre"> </span>for (i = 1, Y[Sa[0]] = 0, p = 1; i < len; ++i) Y[Sa[i]] = my_cmp(X, Sa[i - 1], Sa[i], j) ? p - 1 : p++; for (i = 0; i < len; ++i) X[i] = Y[i];
ok... 后缀数组差不多就这么多啦~ 下篇博客我们讨论如何运用后缀数组解决字符串相关问题