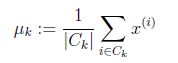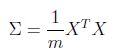Machine Learning week 8 programming exercise K-means Clustering and Principal Component Analysis

K-means Clustering

Implementing K-means

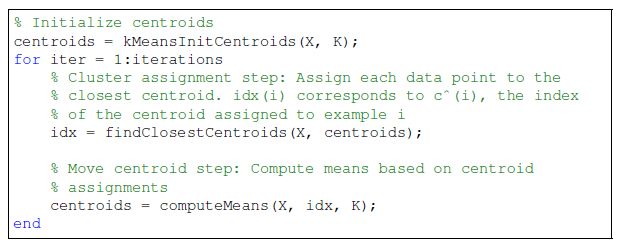
K-means 算法是一个循环算法，需要进行多次循环计算。并且有可能最后得到局部最优解，下面是算法的过程

第一步是cluster assignment，给每个training example找到最近的centroid点，然后确定分类index

function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
%   idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
%   in idx for a dataset X where each row is a single example. idx = m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%

% Set K
K = size(centroids, 1);

% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
%               the index inside idx at the appropriate location.
%               Concretely, idx(i) should contain the index of the centroid
%               closest to example i. Hence, it should be a value in the 
%               range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%
X_k = idx; %选择这种算法是因为不想计算m，给了m的话，肯定就做2层循环了
for i = 1:K,
    X_item = X - centroids(i, :);
    X_item = X_item.*X_item;
    X_item = sum(X_item, 2);%计算出每个点距离k中心点的距离平方
    if i == 1,
        X_k = X_item;
    else
        X_k = [X_k X_item];%最终每行排列的是K个数字，每个数字代表第i个点距离第k个点的距离平方
    end;
end;    

[val, ind] = min(X_k, [], 2); %返回每行的最小值和index
idx = ind;

% =============================================================

end

第二步是根据新的分类情况重新计算各个分类的centroid点，

function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returs the new centroids by computing the means of the 
%data points assigned to each centroid.
%   centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by 
%   computing the means of the data points assigned to each centroid. It is
%   given a dataset X where each row is a single data point, a vector
%   idx of centroid assignments (i.e. each entry in range [1..K]) for each
%   example, and K, the number of centroids. You should return a matrix
%   centroids, where each row of centroids is the mean of the data points
%   assigned to it.
%

% Useful variables
[m n] = size(X);

% You need to return the following variables correctly.
centroids = zeros(K, n);


% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
%               belong to it. Concretely, the row vector centroids(i, :)
%               should contain the mean of the data points assigned to
%               centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%

for i = 1:K,
    k = find(idx==i);%注意这里不要写成一个等号，第一次就写错了
    num = size(k, 1);
    centroids(i,:) = sum(X(k,:),1)/num;
end;





% =============================================================


end

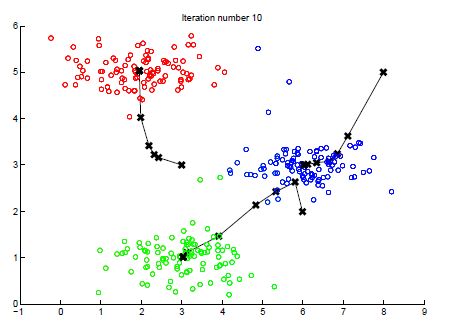
这里进行了10次循环，如果画出每次的变化过程的话

随机初始化，因为有可能会得到局部最优解，所以我们会多次随机初始化初始的centroid点，下面的代码进行了随机初始化，而且通过对training example的随机重新排列，并取其中前k个点，这样可以有效的避免重复元素的出现。

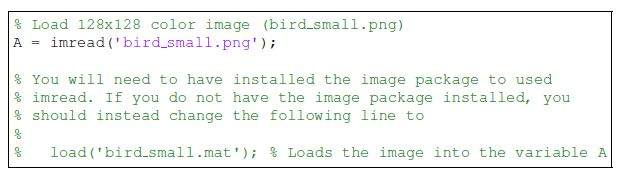
使用K-means算法压缩图像

这张图片的每个像素点都是有3个8bits的数字来分别代表Red，Green，Blue的颜色深度，也就是使用的RGB方法来进行的编码。这里我们使用K-means方法来压缩这个图片，通过k-means方法选出16个颜色，然后使用RGB方法表示这16个颜色，然后每个像素点只需要4bit就可以表示出来是16种元素的那个颜色。这样可以压缩到原来大小的1/6.

octave读图的方法

整个图片会对应一个三维的矩阵，其中前2维分别是点的横纵坐标，最后一维取值1-3，分别代表RGB中三种颜色的深度。扁平化处理之后，每个点会有3个features分别是rgb，然后在这3个feature上进行聚类，最终找到16个点。下图会是最后的结果，明显会有很多失真。

Principal Component Analysis

Implementing PCA

PCA最重要的有两个部分一个是计算covariance(sigma)，另外是通过svd进行分解矩阵获得k个component，然后投影

当然进行PCA之前，我们有必要先对数据进行normalization，

sigma既covariance计算如下，代码十分简单

function [U, S] = pca(X)
%PCA Run principal component analysis on the dataset X
%   [U, S, X] = pca(X) computes eigenvectors of the covariance matrix of X
%   Returns the eigenvectors U, the eigenvalues (on diagonal) in S
%

% Useful values
[m, n] = size(X);

% You need to return the following variables correctly.
U = zeros(n);
S = zeros(n);

% ====================== YOUR CODE HERE ======================
% Instructions: You should first compute the covariance matrix. Then, you
%               should use the "svd" function to compute the eigenvectors
%               and eigenvalues of the covariance matrix. 
%
% Note: When computing the covariance matrix, remember to divide by m (the
%       number of examples).
%

sigma = X'*X/m;
[U, S, V] = svd(sigma);




% =========================================================================

end

Projecting the data onto the principal components

去U的前K列，然后计算投影

function Z = projectData(X, U, K)
%PROJECTDATA Computes the reduced data representation when projecting only 
%on to the top k eigenvectors
%   Z = projectData(X, U, K) computes the projection of 
%   the normalized inputs X into the reduced dimensional space spanned by
%   the first K columns of U. It returns the projected examples in Z.
%

% You need to return the following variables correctly.
Z = zeros(size(X, 1), K);

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the projection of the data using only the top K 
%               eigenvectors in U (first K columns). 
%               For the i-th example X(i,:), the projection on to the k-th 
%               eigenvector is given as follows:
%                    x = X(i, :)';
%                    projection_k = x' * U(:, k);
%

Z = X*U(:, 1:K);


% =============================================================

end

下面是从k维恢复成n的方法

function X_rec = recoverData(Z, U, K)
%RECOVERDATA Recovers an approximation of the original data when using the 
%projected data
%   X_rec = RECOVERDATA(Z, U, K) recovers an approximation the 
%   original data that has been reduced to K dimensions. It returns the
%   approximate reconstruction in X_rec.
%

% You need to return the following variables correctly.
X_rec = zeros(size(Z, 1), size(U, 1));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the approximation of the data by projecting back
%               onto the original space using the top K eigenvectors in U.
%
%               For the i-th example Z(i,:), the (approximate)
%               recovered data for dimension j is given as follows:
%                    v = Z(i, :)';
%                    recovered_j = v' * U(j, 1:K)';
%
%               Notice that U(j, 1:K) is a row vector.
%               

X_rec = Z * U(:, 1:K)';

% =============================================================

end

PCA on Faces

老师给出了一组人脸的数据，分别是32x32的图片，那么我们会有的feature的数量将会是1024个

下面是PCA计算的前36个Component的图像显示

实验中使用了前100个component最为影射空间。然后把所有数据映射到新的100维空间中。这样可以大幅提升计算效率。

我们可以看一看在这个过程中我们损失了哪些信息，可以把数据从100维空间在转化为1024维的数据，当然这里面会有数据丢失，然后看下图，左边是原始数据，右边是恢复的数据。可见我们保留了基本的轮廓，但是细节部分都丢失了