数组的全排列

1.问题背景

学过数学的人都知道，全排列的意思是什么。现在如何用计算机的编程语言实现数组的全排列呢？

数组的全排列可用于求解八皇后问题，具体参见：全排列解决八皇后问题。与此同时，全排列经常会出现在笔试或者面试，如求字符串的全排列。之所以那它作为考题，因为它难度适中，既可以考察递归实现，又能进一步考察非递归的实现，便于区分出考生的水平。所以，掌握它很重要。

2.全排列的递归实现

2.1求解思路

全排列表示把集合中元素的所有按照一定的顺序排列起来，使用P(n, n) = n!表示n个元素全排列的个数。P(n, n)中的第一个n表示元素的个数，第二个n表示取多少个元素进行排列。

给定一个n个元素数组，其全排列的过程可以描述如下：
（1）任意取一个元素放在第一个位置，则有n种选择；
（2）再剩下的n-1个元素中再取一个元素放在第二个位置则有n-1种选择，此时可以看做对n-1个元素进行全排列；
（3）重复第二步，直到对最后一个元素进行全排列，即最后一个元素放在最后一个位置，全排列结束。

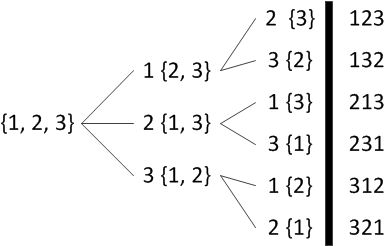
以数组{1,2,3}为例，其全排列的过程如下：
（1）1后面跟（2,3）的全排列；
（2）2后面跟（1,3）的全排列；
（3）3后面跟（1,2）的全排列。

图示如下：

2.2递归实现的优缺点

由于递归将问题逐级分解，因此相对比较容易理解，但是需要消耗大量的栈空间，如果线程栈空间不够，那么就运行不下去了，而且函数调用开销也比较大。

2.3具体实现

#include <iostream>
using namespace std;

int sum=0; //全排列个数

//打印数组内容
void print(int array[],int len){
    printf("{");
    for(int i=0; i<len;++i)
        cout<<array[i]<<" ";
    printf("}\n");
}

//实现两数交换
void swap(int* o,int i,int j){
    int tmp = o[i];
    o[i] = o[j];
    o[j] = tmp;
}

//递归实现数组全排列并打印
void permutation(int array[],int len,int index){
    if(index==len){//全排列结束
        ++sum;
        print(array,len);
    }
    else
        for(int i=index;i<len;++i){
            //将第i个元素交换至当前index下标处
            swap(array,index,i);

            //以递归的方式对剩下元素进行全排列
            permutation(array,len,index+1);

            //将第i个元素交换回原处
            swap(array,index,i);
        }
}

int main(){
    int array[3]={1,2,3};
    permutation(array,3,0);
    cout<<"sum:"<<sum<<endl;

    getchar();
}

运行结果如下：

2.4考虑数组元素中有重复的元素

还是以数组{1,2,3}为例，如果数组中有重复的元素，变成了{1,2,2}，那么它的全排列就不能完全按照上面的方法求解，需要做稍微的改动。

因为全排列是将不同元素依次换到当前位置后，再对后面的元素求全排列。如果将重复的元素多次换到当前位置的话，那么就会出现相同的排列。为了避免，我们禁止将相同的元素多次换到当前位置即可。

例如，对{1，2，2}，第一个数1与第二个数2交换得到212，然后考虑第一个数1与第三个数2交换，此时由于第三个数等于第二个数，所以第一个数不再与第三个数交换。再考虑212，它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。

这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。

修改后的代码如下：

//是否交换
bool isSwap(int array[],int len,int index){
        for(int i=index+1;i<len;++i)
            if(array[index]==array[i])
                return false;
        return true;
}

//递归实现有重复元素的数组全排列
void permutation(int array[],int len,int index){
    if(index==len){//全排列结束
        ++sum;
        print(array,len);
    }
    else
        for(int i=index;i<len;++i){
            if(isSwap(array,len,i)){ //新增判断是否交换
                //将第i个元素交换至当前index下标处
                swap(array,index,i);

                //以递归的方式对剩下元素进行全排列
                permutation(array,len,index+1);

                //将第i个元素交换回原处
                swap(array,index,i);
            }
        }
}

实验结果：

3.全排列的非递归实现

参考文献

[1]http://blog.csdn.net/hackbuteer1/article/details/7462447
[2]http://blog.csdn.net/wangshengfeng1986211/article/details/38366709