Hough变换之直线检测
1.Hough Transform 的算法思想
在直角坐标系和极坐标系中,点、线是对偶关系。
即直角坐标系中的点是极坐标系中的线,直角坐标系中的线是极坐标系中的点。反之也成立。
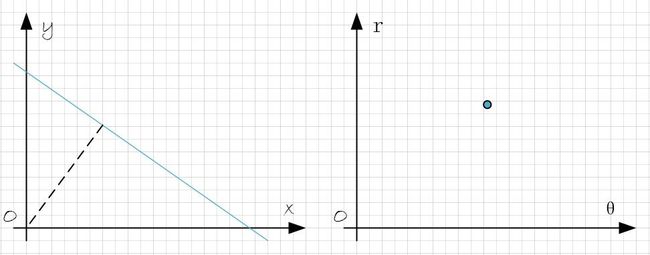
如下图所示,想要检测图像中的直线,可以转化为检测极坐标系中的点 (θ,r) 。
2.Hough空间的表示
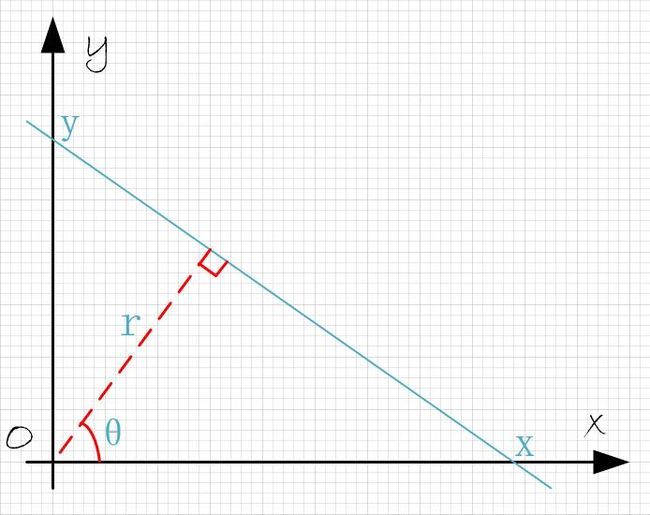
如下图所示,图像中直线的表示,由斜率和截距表示,而极坐标中用 (θ,r) 表示,并且存在下式关系:
r=cos(θ)⋅x+sin(θ)⋅y
对于点
(x0,y0) ,代入上式,在极坐标中就是一条线(很多对
(θ,r) 点):
r=cos(θ)⋅x0+sin(θ)⋅y0
r,θ 就是一对Hough空间的变量表示。
旋转的 θ 不容易表示,若将 r,θ 看成直角坐标空间。一个点 (x0,y0) , 就是一个正弦曲线。
r=cos(θ)⋅x0+sin(θ)⋅y0
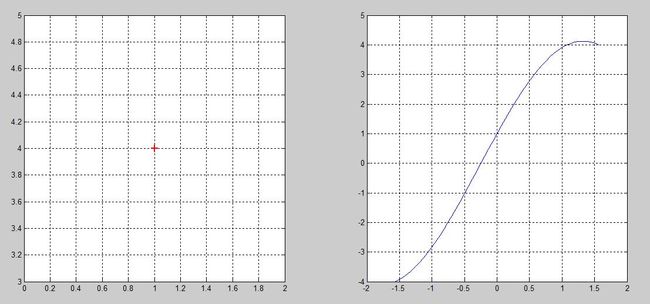
如下图所示,左图直角坐标系中的一个点,对应于右图
r -
θ 空间的一条正弦曲线。
如下图,直角坐标系中的多个点,对应于 r - θ 空间的多条正弦曲线。
直角坐标系的三点共线,对应于 r - θ 空间的多线共点。
因此,我们可以通过检测 r - θ 空间的交集点,来检测原始空间的线段。
接下来,就是要考虑 将 r,θ 离散化,形成离散化的Hough空间,类似于一个矩阵/图像(如下图),用于统计交集点的个数。
3.Hough变换代码分析
以下是使用Matlab进行直线检测的代码。
Hough Transform
首先预处理,转为二值图像:
I = imread('road.jpg');
I = rgb2gray(I);
BW = edge(I,'canny');然后进行霍夫变换:
[H,T,R] = hough(BW,'RhoResolution',0.5,'Theta',-90:0.5:89.5);
imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;检测hough域极值点
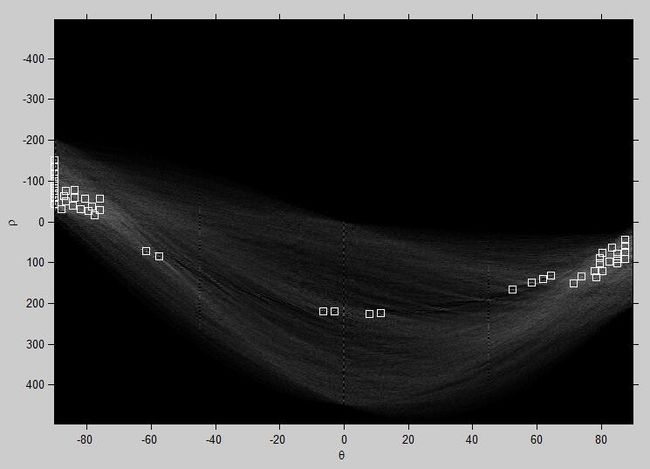
P = houghpeaks(H,50,'threshold',ceil(0.3*max(H(:))));
x = T(P(:,2));
y = R(P(:,1));
plot(x,y,'s','color','white');检测直线
% Find lines and plot them
lines = houghlines(BW,T,R,P,'FillGap',7,'MinLength',100);
figure, imshow(I), hold on
max_len = 0;
for k = 1:length(lines)
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
% plot beginnings and ends of lines
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% determine the endpoints of the longest line segment
len = norm(lines(k).point1 - lines(k).point2);
if ( len > max_len)
max_len = len;
xy_long = xy;
end
end
% highlight the longest line segment
plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','cyan');实验结果
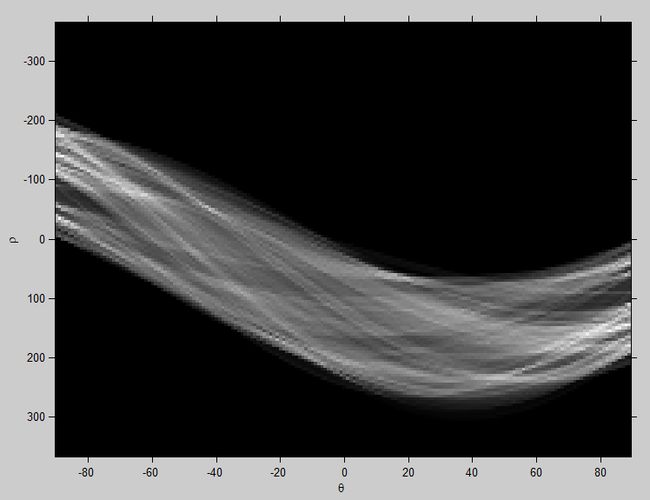
r - θ 空间及前50个极值点:
最终车道直线检测结果:
[注] 所有的代码可以在此处免费下载:http://download.csdn.net/detail/ws_20100/9492054