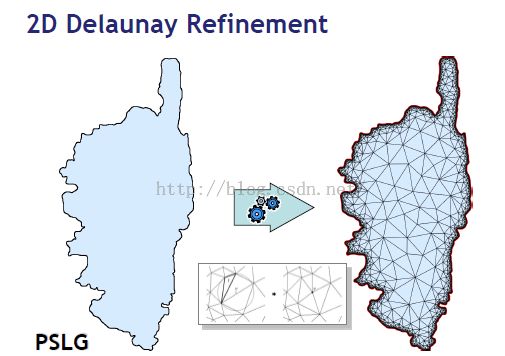
2D Delaunay Refinement (2D Delaunay 细化)
2D 的三角形网格生成
输入:① PSLG C(planar straight line graph):平面直线图
②以C为边界的区域A
输出:区域A的三角形网格T:边C的端点也是网格T的顶点;
边C也是T的组成边;
区域A中的网格T控制着网格的大小和质量。
Key idea:通过插入circumcenters(Voronoi 的顶点),使得三角网格在尺寸和形状上得到破坏。
基本概念(basic notions ):
C:PSLG描述的约束;
T:优化网格。
Respect of the PSLG:
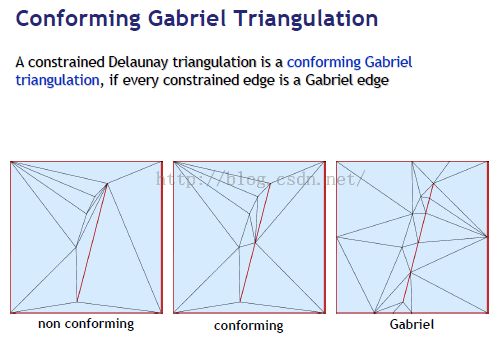
边缘C会一直被分割,直到约束的sub-edges是网格T 的边界;
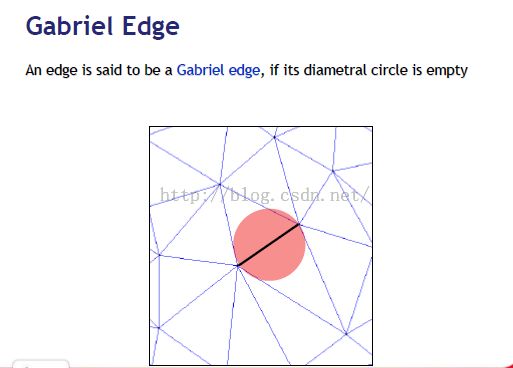
带约束的子边界被要求成为Gabriel edges;
如果三角形最小的外接圆不包括T的顶点,那么 三角形边界则是Gabriel边 ;
边e被点p侵占,如果e最小外接圆不包括点p。
Refinement Algorithm:
C:以PSLG为边界的域(domain)进行网格化分
T:一组当前Delaunay三角的顶点
约束性子边界(Constrained subedges):为边界C的子边界
Initialise with T=Delaunay triangulation of vertices of C (初始化)
Refine until no rule apply:
Rule 1:if there is an encroached constrained subedge e
insert c = midpoint(e) in T(refine-edge) (midpoint 是 subedge e 的中点)
Rule 2:if there ia s bad facet f in ![]() //面的质量不好
//面的质量不好
c = circumcenter (f) //c等于面f的外接圆
if c encroaches a constrained suedge e
refine-edge(e).
else insert(c) in T
Background: