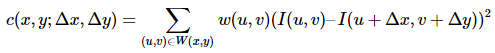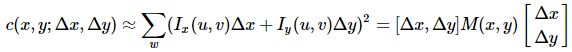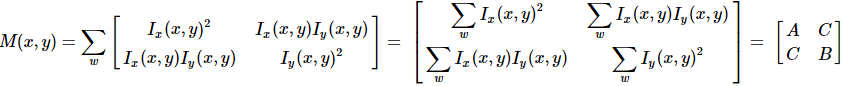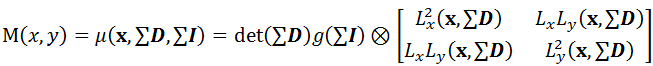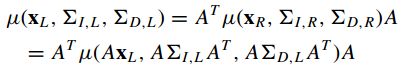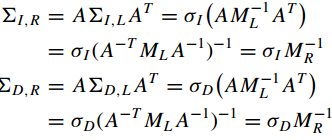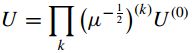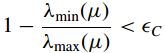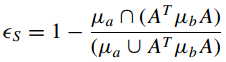尺度及仿射不变的Harris角特征点检测及匹配算法
角特征点检测是一种局部特征子，而局部特征子非常适合于图像匹配及识别（尤其是目标出现阻挡的情况），但问题是如何才能找到具有不变性的特征子（针对于旋转、仿射、光照、尺度等不变性特征）。本文先介绍了经典的Harris角点检测方法，因为Harris方法虽然具有对亮度和对比度的变化不敏感，且具有旋转不变性，但不具有尺度和仿射不变性，所以之后将重点分析一种具有尺度和仿射不变性的Harris改进方法，这个方法是基于Mikolajczyk在2004年发表了论文[Scale & Affine Invariant Interest Point Detectors]。
一、经典的Harris角点检测方法
Harris角点检测是一种非常经典而有效的角点检测方法，它主要是考虑到人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果是在角点位置上的窗口，那么其在各个方向上移动，都会使区域内灰度发生了较大的变化。如果只在一个方向上移动时发生较大变化，那么这点需要是在直线上；如果在各个方向上移动都没有发生变化，那么窗口可能位于平滑的区域。
这里的移动发生变化是由窗口平移后的自相似性来衡量的。
可以简化为：
这其中二阶矩表示为：
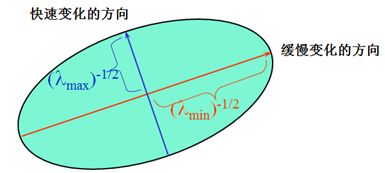
由此可以将自相关函数视为一个椭圆函数：
这个椭圆函数曲线实际上是指这个点附近的等相关线，椭圆曲线上的点同中心点的具有相同的相关程度，其长轴和短轴（可以由二阶矩的特征值来表示）表明了变化快慢的方向。
显然，若是角点的话，那么各方向的变化都比较大，即二阶矩M(x,y)的特征值都较大，且接近相等。可以通过角点响应值cornerness来判断角点，计算每一像素点的角点响应值，并在域内进行非最大值抑制，找到局部最大值即为其角点。
这里的计算主要是用到了二阶矩M(x,y)，使用了微分算子对像素点进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。所以对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量，同时角点判断主要是通过二阶矩M(x,y)的特征值大小来判断的，特征值的方向角完全没有影响，所以Harris方法具有了仿射不变性。
Harris角点检测方法还有一些细节，我也不再详细描述了，因为网上关于Harris方法不仅有详细的代码，还有许多文章写得非常详细，这里推荐一篇文章：http://www.cnblogs.com/ronny/p/4009425.html
二、基于多尺度空间的Harris角点检测方法
Harris角点检测虽然对于光照强度、旋转角度改变具有较好的检测不变性，但是却不具有尺度不变性及仿射不变性，然后在现实生活中，两张图片中目标物体发生尺度变化，或由视点变化而引起仿射变化是非常常见的。为了获得尺度不变性，比较直观的方法就是建立多尺度空间（类似于sift方法），对于每个特征位置都有在不同尺度下的表示，那么在匹配时只要找到对应尺度空间下的特征点就可以了。所以我们只需要在经典的方法里引入多尺度空间，在原特征点空间里增加了多个其他尺度空间的特征点，这些增加的特征点对应于不同的尺度空间的图像，增加了目标尺度变化的鲁棒性，使其具有了一定程度的尺度不变性。由此的新的二阶矩M(x,y)可以表示为：
新的M(x,y)同原来相比增加了两个高斯尺度参数（ σI 称为积分尺度，它是决定Harris角点当前尺度的变量，其越大说明对于尺度越大，有放大效果， σD 为微分尺度或局部尺度，它是决定角点附近微分值变化的变量，实际上可以认为是一个高斯平滑参数，滤除Laplace变换后形成的细小噪声点），另外原来的梯度运算变成了LoG算子（这个算子实际上相当于先进行 高斯平滑滤波，再进行梯度运算）。
然而应用多尺度空间后，会增加大量的特征点，然而特征点的增加会提高误检测的概率及计算复杂度，另外尺度空间的变化并不是连续的，尺度空间变化间隔越少，那么最后匹配的尺度参数与实际尺度的误差越少。因为这个原因，原文里提出了一种自动的尺度参数选择方法。
三、自适应尺度选择的Harris角点检测方法
这个方法主要是找到局部的结构最显著的尺度（原谅我的表达能力>_<，意思就是角点所在结构要个多大的区域才能最好的表示），只需要确定一个显著尺度的特征点，而不需要要原来多个尺度来表示，那么在匹配时只需要将两副图片里目标点分别变换到其显著尺度下，进行匹配就可以了。这里的最显著尺度的衡量是根据所选择的点对应不同尺度LoG响应程度，选择出响应程度最大的尺度（这里的尺度实际上指的是LoG的模板半径，由Ϭ来确定，窗口半径为3Ϭ，即窗口参数）。衡量公式如下：
我们需要找到具有最显著尺度的点和其显著尺度，原文给我们介绍了两种方法，一种是精确的迭代方法，另一种权衡了精确度及计算效率的简化方法：
1、精确的迭代方法：通过迭代方法来选择尺度参数及位置点。已知一个初始的点的位置（从经典Harris方法里选择的每个角点）
及初始尺度参数
，第一步，找到当前点的LoG尺度空间的局部极值尺度参数，这里局部高斯平滑参数
（s为小于1的常数，原文实验参数为0.7），
，尺度空间变化范围是[0.7,1.4]，如果找不到局部极值点，则抛弃。第二步在当前极值尺度下找到与原位置最近的新特征点，反复重复上述两个步骤，直到极值尺度和位置点稳定，即不再发生改变。
2、简化方法：是先建立Harris函数的多尺度空间，然后计算每个尺度里的局部cornerness角程度最大值，作为初始点，然后验证每一个初始点的LoG在尺度坐标上的极值尺度点
，删除那些没有极值或响应太小的点，另外还有可能出现一些点的尺度峰值并不对应于所选择尺度最大，仍然会出现极值尺度误差，所以需要所选择的多尺度的间隔要尽量小，让我们选择的极值尺度接近实际的峰值尺度，以达到高的精确度。这种方法同前面不太一样的是，其并不是每个迭代步骤同时确定每点尺度及位置，而是先确定该位置点所有可以尺度的LoG响应，然后估计其是否存在显著尺度。
一旦当我们确定了峰值尺度，那么当出现多尺度匹配的情况时，只需要将不同图片的特征点先各自变换到其峰值尺度下（归一化操作），然后进行的相互匹配了，从而即满足了尺度不变性，又减少了特征点数目。
四、增加仿射不变性的Harris角点检测方法
图像结构发生仿射变换，同尺度变化不同的是，其各方向变化不同anisotropic（换而言之，尺度变化像圆一样放大缩小，而仿射变化像椭圆一样，各个方向缩放的程度不一样）。我们考虑的是先估计仿射变化矩阵，然后利用原来所估计仿射变化矩阵将仿射后的点或区域还原成各方向变化相同，即类似于仿射变化先转换为尺度变化，然后应用上面的多尺度Harris方法。
同先前的分析一样，我们首先要确定的是二阶矩M(x,y)，新的可以表示为：
由于各方向变化不一样，所以同先前二阶矩不一样的是，这里是协方差而不是方差，为了计算二阶矩M(x,y)，我们首先要计算的协方差和
，这里为了减少计算量，我们可以让，这里的s仍然是个小于1的常数，实验设置为0.7。
为进一步估计的值，我们先假设存在一个线性变换矩阵为A，满足
。那么就有：
即是：
高斯核的协方差（无论
）都可以表示为如下：
通过上面，我们可假设二阶矩可以由下面来计算：
由此，同理我们可以得到：
由此我们可以计算出归一化仿射矩阵A
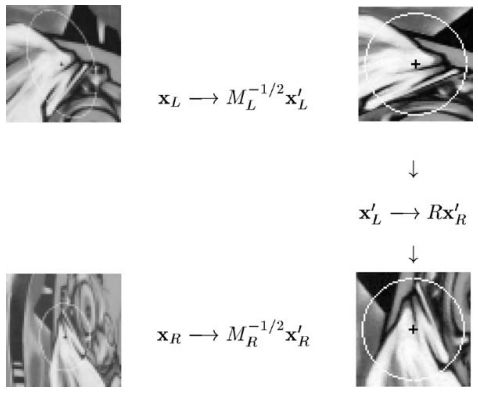
这里的R实际上相当于一个旋转矩阵，相当于整体尺度上变化，
相当于发生仿射变化，大概的示意图如下：
所以我们现在的问题就是如何去估计和
了。
五、Harris仿射兴趣点检测方法
下面我们介绍一种迭代的方法，首先定义一个U变换操作：
k是迭代次数，U初始化为单位矩阵，这里的μ是指每次迭代过程中计算当前点二阶矩M(x,y)。这里的在k次迭代中，先通过应用下列的U变换（首先我们要对初始的图像进行归一化，使U的最大特征值为1，从而确保U变换只往其最小特征值方向增长），窗口大小为W，中心为兴趣点，再利用前面的式子计算当前二阶矩μ，而二阶矩的选择μ是由两个尺度和
决定的，所以我们需要在每次迭代过程中选择这两个尺度参数
和
，随着迭代次数的增加，每次U变换都会使得μ的最小特征值增大，最终接近于最大特征值。
积分尺度参数，主要是用来衡量尺度的，它的选择方法就是我们前面介绍的自适应尺度选择的方法。由于仿射变化的原因，尺度在不同方向的改变是不同的，因此我们需要在每次进行U变换后，这些点如上面进的尺度自适应方法一样，都逐渐收敛到尺度和二阶矩（实际上是位置点）都不再改变。
是我们假设的为
，s是个小于1的常数。局部尺度参数
极大地影响了二阶矩μ的收敛性，因为这个迭代过程是为了达到一个具有相等特征值的矩阵U，特征值之间差别越小，就越接近最终结果，收敛速度也越快。而前面的角程度已经找到那些具有两个大的特征值二阶矩μ的兴趣点。而特征值之间差别越大，那么在U变换后将会造成一方面形成巨大的增加，所以不会收敛到一个稳定的U变换。局部尺度参数的选择可以平滑滤波，减少噪声，从而保证一个合适的特征值比，以确保收敛。
每次迭代后，先进行U变换：
这里的为U变化图像窗口里的空间坐标。首先，重新检测U变换后归一化窗口的最大值，然后可以获得原兴趣点指向最近最大值的向量
，然后对这个向量重新应用U变化，获得新点位置
。
最终的收敛条件：
1、二阶矩μ的两个特征值接近：
2、将U变换矩阵分解成，这里的R是旋转矩阵，D是尺度变换矩阵，为减少迭代陷入死循环，我们需要排除一些特征值比值太大的点，这些点容易造成不稳定的点。
六、检测算法总结
满足
相似仿射点的选择问题：因为归一化后的区域是各方向变化同样的，因为存在这样的可能，多个兴趣点都指向同一个特征，但从不同尺度水平中检测出来却最终收敛于一个点的位置和尺度。为了区分这些点，可以通过比较其位置
、尺度
、伸缩比
，及倾斜度由
里的R获得。如果所有的这些参数都同参考值非常接近的，就可以认为这个点相似的，最后我们可以从鉴定点集里，平均这些参数，选择最相似的点，最后我们会得一个每点都代表着不同的图像位置及结构的点集。
在这张图里，（a）图里的白色圆是指不同尺度下特征点位置，而黑色圆是选择的最显著的尺度。（b）图里黑色圆指检测出来仿射区域，而白色圆是指与之对应图像在其上的投影区域，（c）图说明了多个不同尺度的兴趣点最终收敛到同样的尺度及位置的情况，（d）图里黑色圆对这些兴趣点参数进行了平均，而白色圆是指与之对应图像在其上的投影区域。（e）归一化后的区域。
兴趣点的衡量与估计：
1、 位置偏差
这里的
分别指两张图片里同一兴趣点的不同位置，H指其变化矩阵。
2、区域重叠性
都是指两张兴趣点附近的椭圆区域，满足
七、特征点匹配问题
给定一个图片，我们检测出一定兴趣点集，然后计算特征点的描述子，而描述子能过相似性衡量来比较。点检测出来后，新问题就是如何获得特征点描述子，以用于后期的匹配算法，为了让匹配也具有各种不变性特征，这同时也要求描述子本身也要具有旋转不变性及仿射不变性特征。sift方法里面的描述子具有了一定程度的旋转及仿射不变性。
本文的描述子也是通过计算特征点的邻域的高斯微分，这个微分可以通过在被U变换归一化的图像块里计算，这里的U变换对于每一特征点来说都是不相同的，排除仿射变化及尺度变化的影响。旋转不变性可以通过在梯度方向上进行微分，为了获得梯度方向上的稳定估计，通过平均邻域的梯度方向，获得一个基准方向，然后将整个邻域旋转来基准主方向来，同sift方法非常类似。