hdoj 2036 改革春风吹满地

改革春风吹满地

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 22826    Accepted Submission(s): 11809

Problem Description

“ 改革春风吹满地,
不会AC没关系;
实在不行回老家，
还有一亩三分地。
谢谢!（乐队奏乐）”

话说部分学生心态极好，每天就知道游戏，这次考试如此简单的题目，也是云里雾里，而且，还竟然来这么几句打油诗。
好呀，老师的责任就是帮你解决问题，既然想种田，那就分你一块。
这块田位于浙江省温州市苍南县灵溪镇林家铺子村，多边形形状的一块地，原本是linle 的，现在就准备送给你了。不过，任何事情都没有那么简单，你必须首先告诉我这块地到底有多少面积，如果回答正确才能真正得到这块地。
发愁了吧？就是要让你知道，种地也是需要AC知识的！以后还是好好练吧...

 

Input

输入数据包含多个测试实例，每个测试实例占一行，每行的开始是一个整数n(3<=n<=100)，它表示多边形的边数（当然也是顶点数），然后是按照逆时针顺序给出的n个顶点的坐标（x1, y1, x2, y2... xn, yn）,为了简化问题，这里的所有坐标都用整数表示。
输入数据中所有的整数都在32位整数范围内，n=0表示数据的结束，不做处理。

 

Output

对于每个测试实例，请输出对应的多边形面积，结果精确到小数点后一位小数。
每个实例的输出占一行。

 

Sample Input

   
   
   
   

    
    
    
    3 0 0 1 0 0 1
4 1 0 0 1 -1 0 0 -1
0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    0.5
2.0
   
   
   
   

 

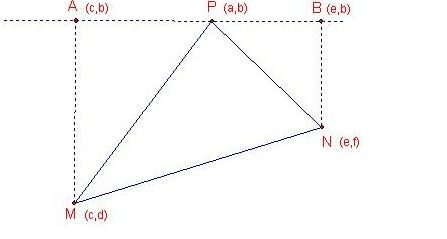
已知直角坐标系3点p(a,b),m(c,d),n(e,f) 求三角形pmn面积的表达式！ 

解：

无论三角形的顶点位置如何，△PMN总可以用一个直角梯形（或矩形）和两个直角三角形面积的和差来表示
而在直角坐标系中，已知直角梯形和直角三角形的顶点的坐标，其面积是比较好求的。
下面以一种情形来说明这个方法，其它情形方法一样，表达式也一样（表达式最好加上绝对值，确保是正值）
如图情形（P在上方，M在左下，N在右下），过P作X轴的平行线L，作MA⊥L，NB⊥L（设P在A、B之间）
则A、B的坐标是A(c,b)，B(e,b)
所以PA＝a－c,PB＝e－a,AM＝b－d,BN＝b－f,AB＝e－c
所以S△PMN＝S梯形AMNB－S△PAM－S△PBN
＝(b－d＋b－f)(e－c)/2－(b－d)(a－c)/2－(b－f)(e－a)/2
＝(ad＋be＋cf－af－bc－de)/2

//任意多边形都可以转化为n个三角形的面积和

#include <iostream>
#include <iomanip>
using namespace std;
int x[100],y[100];
float s(int a,int b,int c,int d,int e,int f)
{
    return (a*d+c*f+b*e-e*d-c*b-a*f)/2.0;
}
int main()
{
    int n;
    while(cin>>n&&n!=0)
    {
        float res=0;
        for(int i=0; i<n; i++)
            cin>>x[i]>>y[i];
        for(int i=0; i<n-2; i++)
        {
            res=res+s(x[0],y[0],x[i+1],y[i+1],x[i+2],y[i+2]);
        }
        printf("%.1f\n",res);
    }
    return 0;
}