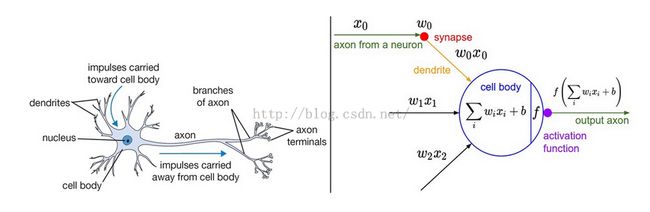
Deep Neural Networks的Tricks
Here we will introduce these extensive implementation details, i.e., tricks or tips, for building and training your own deep networks.
主要以下面八个部分展开介绍：
mainly in eight aspects: 1) data augmentation; 2) pre-processing on images; 3) initializations of Networks; 4) some tips during training; 5) selections of activation functions; 6) diverse regularizations; 7)some insights found from figures and finally 8) methods of ensemble multiple deep networks.
1，数据扩增
2.预处理数据
3.初始化网络
4，在训练中的一些tips
5,合理的选择激活函数
6.多种正则化
7，从实验图和结果发现insights
8，如何集合多个网络
依次介绍八种方法：
一、data augmentation
1. th additiarhorizontally flipping（水平翻转）, random crops(随机切割) and color jittering(颜色抖动). Moreover, you could try combinations of multiple different processing, e.g., doing the rotation and random scaling at the same time. In addition, you can try to raise saturation and value (S and V components of the HSV color space) of all pixels to a power between 0.25 and 4 (same for all pixels within a patch), multiply these values by a factor between 0.7 and 1.4, and add to them a value between -0.1 and 0.1. Also, you could add a value between [-0.1, 0.1] to the hue (H component of HSV) of all pixels in the image/patch.
2、Krizhevsky et al. [1] proposed fancy PCA。you can firstly perform PCA on the set of RGB pixel values throughout your training images. add the following quantity to each RGB image pixel (i.e., ![I_{xy}=[I_{xy}^R,I_{xy}^G,I_{xy}^B]^T](http://img.e-com-net.com/image/info5/8d608362259e46519d6c49f7d6cd6f1e.png){kind=small}
): ![bf{p}_1,bf{p}_2,bf{p}_3][alpha_1 lambda_1,alpha_2 lambda_2,alpha_3 lambda_3]^T](http://img.e-com-net.com/image/info5/c35dcb9098694b729de3090f22da0269.png){kind=small}
where, 
and 
are the -th eigenvector and eigenvalue of the 
covariance matrix of RGB pixel values, respectively, and is a random variable drawn from a Gaussian with mean zero and standard deviation 0.1. 。。
二、Pre-processing
1、The first and simple pre-processing approach is zero-center the data, and then normalize them。
code：
>>> X -= np.mean(X, axis = 0) # zero-center >>> X /= np.std(X, axis = 0) # normalize
2、re-processing approach similar to the first one is PCA Whitening.
>>> X -= np.mean(X, axis = 0) # zero-center >>> cov = np.dot(X.T, X) / X.shape[0] # compute the covariance matrix
>>> U,S,V = np.linalg.svd(cov) # compute the SVD factorization of the data covariance matrix >>> Xrot = np.dot(X, U) # decorrelate the data
>>> Xwhite = Xrot / np.sqrt(S + 1e-5) # divide by the eigenvalues (which are square roots of the singular values)
上面两种方法：these transformations are not used with Convolutional Neural Networks. However, it is also very important to zero-center the data, and it is common to see normalization of every pixel as well.
三、初始化-Initialization
1.All Zero Initialization---假如全部权值都设为0或相同的数，就会计算相同梯度和相同的参数更新，即没有对称性
2、Initialization with Small Random Numbers
is a zero mean, unit standard deviation gaussian. It is also possible to use small numbers drawn from a uniform distribution, but this seems to have relatively little impact on the final performance in practice.
One problem with the above suggestion is that the distribution of the outputs from a randomly initialized neuron has a variance that grows with the number of inputs. It turns out thatyou can normalize the variance of each neuron's output to 1 by scaling its weight vector by the square root of its fan-in (i.e., its number of inputs), which is as follows:
>>> w = np.random.randn(n) / sqrt(n) # calibrating the variances with 1/sqrt(n)
As aforementioned, the previous initialization by calibrating the variances of neurons is without considering ReLUs. A more recent paper on this topic by He et al. [4] derives an initialization specifically for ReLUs, reaching the conclusion that the variance of neurons in the network should be as:
>>> w = np.random.randn(n) * sqrt(2.0/n) # current recommendation
K. He, X. Zhang, S. Ren, and J. Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. InICCV, 2015.
) and small strides (e.g., 1) with zeros-padding, which not only reduces the number of parameters, but improves the accuracy rates of the whole deep network. Meanwhile, a special case mentioned above, i.e., filters with stride 1, could preserve the spatial size of images/feature maps. For the pooling layers, the common usedpooling size is of .
本图取之：http://cs231n.stanford.edu/index.html
几种激活函数：
Sigmoid：
The sigmoid non-linearity has the mathematical form . It takes a real-valued number and “squashes” it into range between 0 and 1. In particular, large negative numbers become 0 and large positive numbers become 1. The sigmoid function has seen frequent use historically since it has a nice interpretation as the firing rate of a neuron: from not firing at all (0) to fully-saturated firing at an assumed maximum frequency (1).在最大阈值1时，就达到饱和--Saturated.
sigmoid已经失宠，因为他的两个缺点：
（1）.Sigmoids saturate and kill gradients. 由于饱和而失去了梯度
因为在when the neuron's activation saturates at either tail of 0 or 1, the gradient at these regions is almost zero。看图就知道，整个曲线的倾斜角度，在两端倾斜角都是平的。
关键的问题在于this (local) gradient will be multiplied to the gradient of this gate's output for the whole objective。这样就会因为local gradient 太小，而it will effectively “kill” the gradient and almost no signal will flow through the neuron to its weights
and recursively to its data. 影响到梯度，导致没有信号能通过神经元传递给权值。而且还需要小心关注初始权值，one must pay extra caution when initializing the weights of sigmoid neurons to prevent saturation. For example, if the initial weights are too large then most neurons would become saturated and the network will barely learn.因为初始的权值太大，就会让神经元直接饱和，整个网络难以学习。
(2) .Sigmoid outputs are not zero-centered. 不是以0为中心
This is undesirable since neurons in later layers of processing in a Neural Network (more on this soon) would be receiving data that isnot zero-centered. This has implications on the dynamics duringgradient descent, because if the data coming into a neuron is always positive(e.g., element wise in 
), then the gradient on the weights will during back-propagation become either all be positive, or all negative(depending on the gradient of the whole expression 
).
这样在后几层网络中接受的值也不是0中心，这样在动态梯度下降法中，如果进入nueron中的数据都是正的，那么整个权值梯度w要不全为正，或者全为负（取决于f的表达形式）。
This could introduce undesirable zig-zagging dynamics in the gradient updates for the weights. However, notice that once these gradients are added up across a batch of data the final update for the weights can have variable signs, somewhat mitigating this issue. Therefore, this is an inconvenience but it has less severe consequences compared to the saturated activation problem above.
这回导致锯齿状的动态梯度，但如果在一个batch数据中将梯度求和来更新权值，有可能会相互抵消，从而缓解上诉的影响。这笔饱和激活带来的影响要轻太多了！
Tanh(x)
The tanh non-linearity squashes a real-valued number to the range [-1, 1]. Like the sigmoid neuron, its activations saturate, but unlike the sigmoid neuron its output is zero-centered. Therefore, in practice the tanh non-linearity is always preferred to the sigmoid nonlinearity.
tanh的作用是将真个实数数据放到了[-1,1]之间，他的激活依旧是饱和状态，但他的输出是0中心。
Rectified Linear Unit
There are several pros and cons to using the ReLUs:
-
(Pros) Compared to sigmoid/tanh neurons that involve expensive operations (exponentials, etc.), the ReLU can be implemented by simply thresholding a matrix of activations at zero. Meanwhile, ReLUs does not suffer from saturating.
运算简单，非指数形式，切不会饱和
-
(Pros) It was found to greatly accelerate (e.g., a factor of 6 in [1]) the convergence of stochastic gradient descent compared to the sigmoid/tanh functions. It is argued that this is due to its linear, non-saturating form.
已被证明可以加速随机梯度收敛，被认为是由于其线性和非饱和形式（有待考证）
-
(Cons) Unfortunately, ReLU units can be fragile during training and can “die”. For example, a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again. If this happens, then the gradient flowing through the unit will forever be zero from that point on. That is, the ReLU units can irreversibly die during training since they can get knocked off the data manifold. For example, you may find that as much as 40% of your network can be “dead” (i.e., neurons that never activate across the entire training dataset) if the learning rate is set too high. With a proper setting of the learning rate this is less frequently an issue.
Leaky ReLUs are one attempt to fix the “dying ReLU” problem. Instead of the function being zero when , a leaky ReLU will instead have a small negative slope (of 0.01, or so). That is, the function computes if and if , where is a small constant. Some people report success with this form of activation function, but the results are not always consistent. 修改了x<0部分，设定为了一个常数a,
后续又出来了一连串的RELU的修改：
ReLU, Leaky ReLU, PReLU and RReLU. In these figures, for PReLU, is learned and for Leaky ReLU is fixed. For RReLU, 
is a random variable keeps sampling in a given range, and remains fixed in testing.
PReLU的a是学习得到，RReLU的a是随机采样变换。在测试中是固定。
-
B. Xu, N. Wang, T. Chen, and M. Li. Empirical Evaluation of Rectified Activations in Convolution Network. In ICML Deep Learning Workshop, 2015.
From these tables, we can find the performance of ReLU is not the best for all the three data sets. For Leaky ReLU, a larger slope will achieve better accuracy rates. PReLU is easy to overfit on small data sets (its training error is the smallest, while testing error is not satisfactory), but still outperforms ReLU. In addition, RReLU is significantly better than other activation functions on NDSB, which shows RReLU can overcome overfitting, because this data set has less training data than that of CIFAR-10/CIFAR-100. In conclusion, three types of ReLU variants all consistently outperform the original ReLU in these three data sets. And PReLU and RReLU seem better choices. Moreover, He et al. also reported similar conclusions in [4]
[4]K. He, X. Zhang, S. Ren, and J. Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. InICCV, 2015.
Regularizations
There are several ways of controlling the capacity of Neural Networks to prevent overfitting:
-
L2 regularization is perhaps the most common form of regularization. It can be implemented by penalizing the squared magnitude of all parameters directly in the objective. That is, for every weight in the network, we add the term to the objective, where
is the regularization strength. It is common to see the factor of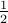 
in front because then the gradient of this term with respect to the parameter is simply instead of . The L2 regularization has the intuitive interpretation of heavily penalizing peaky weight vectors and preferring diffuse weight vectors. -
L1 regularization is another relatively common form of regularization, where for each weight we add the term to the objective. It is possible to combine the L1 regularization with the L2 regularization: (this is called Elastic net regularization). The L1 regularization has the intriguing property that it leads the weight vectors to become sparse during optimization (i.e. very close to exactly zero). In other words, neurons with L1 regularization end up using only a sparse subset of their most important inputs and become nearly invariant to the “noisy” inputs. In comparison, final weight vectors from L2 regularization are usually diffuse, small numbers. In practice, if you are not concerned with explicit feature selection, L2 regularization can be expected to give superior performance over L1.
-
Max norm constraints. Another form of regularization is to enforce an absolute upper bound on the magnitude of the weight vector for every neuron and use projected gradient descent to enforce the constraint. In practice, this corresponds to performing the parameter update as normal, and then enforcing the constraint by clamping the weight vector
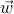of every neuron to satisfy 
. Typical values of 
are on orders of 3 or 4. Some people report improvements when using this form of regularization. One of its appealing properties is that network cannot “explode” even when the learning rates are set too high because the updates are always bounded. -
Dropout is an extremely effective, simple and recently introduced regularization technique by Srivastava et al. in [6] that complements the other methods (L1, L2, maxnorm). During training, dropout can be interpreted as sampling a Neural Network within the full Neural Network, and only updating the parameters of the sampled network based on the input data. (However, the exponential number of possible sampled networks are not independent because they share the parameters.) During testing there is no dropout applied, with the interpretation of evaluating an averaged prediction across the exponentially-sized ensemble of all sub-networks (more about ensembles in the next section). In practice, the value of dropout ratio
is a reasonable default, but this can be tuned on validation data.
N. Srivastava, G. E. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. JMLR, 15(Jun):1929−1958, 2014.
七：ome insights found from figures and finally训练中重要的图
1.As we have known, the learning rate is very sensitive. From Fig. 1 in the following, a very high learning rate will cause a quite strange loss curve. A low learning rate will make your training loss decrease very slowly even after a large number of epochs. In contrast, a high learning rate will make training loss decrease fast at the beginning, but it will also drop into a local minimum. Thus, your networks might not achieve a satisfactory results in that case. For a good learning rate, as the red line shown in Fig. 1, its loss curve performs smoothly and finally it achieves the best performance.
不同的LR设定会带来不同的Loss效果，需要合理的选择一个lr
2.
-
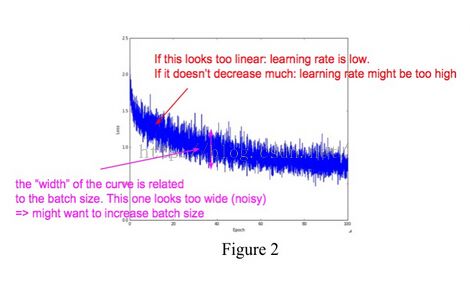
Now let’s zoom in the loss curve. The epochs present the number of times for training once on the training data, so there are multiple mini batches in each epoch. If we draw the classification loss every training batch, the curve performs like Fig. 2. Similar to Fig. 1, if the trend of the loss curve looks too linear, that indicates your learning rate is low; if it does not decrease much, it tells you that the learning rate might be too high. Moreover, the “width” of the curve is related to the batch size. If the “width” looks too wide, that is to say the variance between every batch is too large, which points out you should increase the batch size.
每一个epoch中又多个batchsize的循环。下图纵坐标是loss,横坐标是epoch，每一个epoch纵向蓝色直线就是 一个循环epoch内每个Batchsize对应的Loss。如果看起来太线性说明Lr太低，如果没有降低太多，说明Lr太高。整个蓝色直线的width与batch size的大小有关，如果她看着太宽了，可能就需要增加batch size, 这样就会降低width==num/batchsize.
3.
-
Another tip comes from the accuracy curve. As shown in Fig. 3, the red line is the training accuracy, and the green line is the validation one. When the validation accuracy converges, the gap between the red line and the green one will show the effectiveness of your deep networks. If the gap is big, it indicates your network could get good accuracy on the training data, while it only achieve a low accuracy on the validation set. It is obvious that your deep model overfits on the training set. Thus, you should increase the regularization strength of deep networks. However, no gap meanwhile at a low accuracy level is not a good thing, which shows your deep model has low learnability. In that case, it is better to increase the model capacity for better results.再说test data与 validation data之间的关系，gap太大，就导致了overfitting。
八：Ensemble
In machine learning, ensemble methods [8] that train multiple learners and then combine them for use are a kind of state-of-the-art learning approach. It is well known that an ensemble is usually significantly more accurate than a single learner, and ensemble methods have already achieved great success in many real-world tasks. In practical applications, especially challenges or competitions, almost all the first-place and second-place winners used ensemble methods.
Here we introduce several skills for ensemble in the deep learning scenario.
-
Same model, different initialization. Use cross-validation to determine the best hyperparameters, then train multiple models with the best set of hyperparameters but with different random initialization. The danger with this approach is that the variety is only due to initialization.
-
Top models discovered during cross-validation. Use cross-validation to determine the best hyperparameters, then pick the top few (e.g., 10) models to form the ensemble. This improves the variety of the ensemble but has the danger of including suboptimal models. In practice, this can be easier to perform since it does not require additional retraining of models after cross-validation. Actually, you could directly select several state-of-the-art deep models from Caffe Model Zoo to perform ensemble.
-
Different checkpoints of a single model. If training is very expensive, some people have had limited success in taking different checkpoints of a single network over time (for example after every epoch) and using those to form an ensemble. Clearly, this suffers from some lack of variety, but can still work reasonably well in practice. The advantage of this approach is that is very cheap.
-
Some practical examples. If your vision tasks are related to high-level image semantic, e.g., event recognition from still images, a better ensemble method is to employ multiple deep models trained on different data sources to extract different and complementary deep representations. For example in the Cultural Event Recognition challenge in associated with ICCV’15, we utilized five different deep models trained on images of ImageNet, Place Database and the cultural images supplied by the competition organizers. After that, we extracted five complementary deep features and treat them as multi-view data. Combining “early fusion” and “late fusion” strategies described in [7], we achieved one of the best performance and ranked the 2nd place in that challenge. Similar to our work,[9] presented the Stacked NN framework to fuse more deep networks at the same time.
In real world applications, the data is usually class-imbalanced: some classes have a large number of images/training instances, while some have very limited number of images.
类别不平均问题： 一些类拥有大量的训练数据，一类数据量有限
As discussed in a recent technique report [10], when deep CNNs are trained on these imbalanced training sets, the results show that imbalanced training data can potentially have a severely negative impact on overall performance in deep networks.
不平衡的训练数据对整个网络有负面效果
For this issue, the simplest method is to balance the training data by directly up-sampling and down-sampling the imbalanced data, which is shown in [10].
一种解决方法：直接上采样和下采样数据，
Another interesting solution is one kind of special crops processing in our challenge solution [7]. Because the original cultural event images are imbalanced, we merely extract crops from the classes which have a small number of training images, which on one hand can supply diverse data sources, and on the other hand can solve the class-imbalanced problem.
另一种:解决办法如文献{7}中，采用剪切的办法
[7]X.-S. Wei, B.-B. Gao, and J. Wu. Deep Spatial Pyramid Ensemble for Cultural Event Recognition. In ICCV ChaLearn Looking at People Workshop, 2015.
In addition, you can adjust the fine-tuning strategy for overcoming class-imbalance. For example, you can divide your own data set into two parts: one contains the classes which have a large number of training samples (images/crops); the other contains the classes of limited number of samples. In each part, the class-imbalanced problem will be not very serious. At the beginning of fine-tuning on your data set, you firstly fine-tune on the classes which have a large number of training samples (images/crops), and secondly, continue to fine-tune but on the classes with limited number samples.
第三种方法：采用fine-tuning策略，将数据分割为两个部分，大数据集合小数据集，先微调大的类，再微调小类。
[10] P. Hensman, and D. Masko. The Impact of Imbalanced Training Data for Convolutional Neural Networks. Degree Project in Computer Science, DD143X, 2015.
References & Source Links
-
A. Krizhevsky, I. Sutskever, and G. E. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. In NIPS, 2012
-
A Brief Overview of Deep Learning, which is a guest post by Ilya Sutskever.
-
CS231n: Convolutional Neural Networks for Visual Recognition of Stanford University, held by Prof. Fei-Fei Li and Andrej Karpathy.
-
K. He, X. Zhang, S. Ren, and J. Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In ICCV, 2015.
-
B. Xu, N. Wang, T. Chen, and M. Li. Empirical Evaluation of Rectified Activations in Convolution Network. In ICML Deep Learning Workshop, 2015.
-
N. Srivastava, G. E. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. JMLR, 15(Jun):1929−1958, 2014.
-
X.-S. Wei, B.-B. Gao, and J. Wu. Deep Spatial Pyramid Ensemble for Cultural Event Recognition. In ICCV ChaLearn Looking at People Workshop, 2015.
-
Z.-H. Zhou. Ensemble Methods: Foundations and Algorithms. Boca Raton, FL: Chapman & HallCRC/, 2012. (ISBN 978-1-439-830031)
-
M. Mohammadi, and S. Das. S-NN: Stacked Neural Networks. Project in Stanford CS231n Winter Quarter, 2015.
-
P. Hensman, and D. Masko. The Impact of Imbalanced Training Data for Convolutional Neural Networks. Degree Project in Computer Science, DD143X, 2015.
参考：http://blog.csdn.net/pandav5/article/details/51178032
http://blog.csdn.net/u010025211/article/details/51202236