由一个日期(年月日),怎样知道是星期几?和由此开始的有趣事情
如何由一个日期,获得那天是星期几?Tomohiko Sakamoto提供了优雅的代码
int dayofweek(int y, int m, int d) /* 0 = Sunday */
{
int t[]= {0, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4};
y -= m < 3;
return (y + y/4 - y/100 + y/400 + t[m-1] + d) % 7;
}
关于这段代码的解释见于《Tomohiko Sakamoto 星期计算算法推导 》一文,本来到这里就结束了,但我在研究这段代码的时候,事情变得有趣起来。
消失的十天
我测试了好多值,这些值都是1900年以后的,结果都是正确的。但我发现年数比较小的时候,就不正确了。
我就在找到底是哪一天开始出问题了,最后我找到了问题所在。
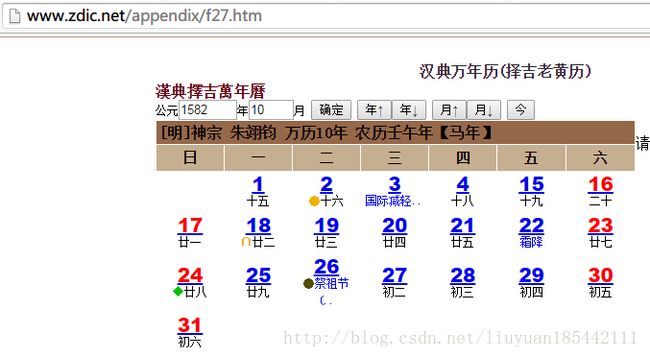
看到没,1582年10月4日之后直接就是15日了!而且从另外一个来源查询的结果也是这样!莫非它们用的是同一个算法,所以出了同样的错误?
我开始搜索1582年10月4日,最终找到了答案。
历法之变
公元前46年,儒略·恺撒掌握古罗马帝国军政大权后,聘请了天文学家索西琴改革历法,其要点是:
1、全年12个月,单月为大月31天,双月为小月30天,平年的二月为29天,全年共计365天;
2、冬至后十月为一年的开始,即为每年的岁首;
3、从改历的下一年起,每三年是一闰年,闰年共计366天,所多的一天放在二月尾,为30天。
这就是现行流行的阳历的前身,一般称“儒略历”,其中七月因儒略·恺撒的出生而命名为“儒略月”。
然而负责执行的僧侣们误把“每隔三年置一闰年”理解为“每三年置一闰年”,并一直错误执行了三十多年,到公元前九年屋大维(即奥古斯都)统治时,人们发现三十多年中已多设置了闰年五次,于是屋大维下令在以后的一段年份里少设三次闰年,并恢复原来每四年设置一闰的规定。
屋大维是把自己的出生的八月命名为奥古斯都月,于是把原来属于小月的八月改为大月,多出的一天从二月中扣出。同时,为了避免一连三个大月,又把九月和十一月改为小月,十月和十二月改为大月。这一不合理的规定一直延续到现在。
地球公转一周的时间是365.2422日(即365天5时48分46秒),儒略历规定每年平均长度是365.25天,比实际回归年长出0.0078天,即每年长出12分14秒。这点差值在短期内难以发现,但只要过128年,历法规定的年就要多出回归年一天。
公元325年,欧洲基督教教会召开宗教大会,一致确定儒略历是最准确的历法并全面推行。并根据天文观测和宗教活动的需要,规定春分日必须是三月二十一日,而纪念耶稣死后复活的复活节定在春分满月后的第一个星期日,到公元1582年,随着哥白尼太阳中心说的确认和天文观测的技术的进步,发现实际春分时刻已提前到三月十一日,比原定的三月二十一日提前十天,当时的罗马教皇格列高列十三世便召集天文学者和僧侣们商讨改历问题,最后决定采用天文学家利里奥的改革方案。
1、为使春分时刻再回到三月二十一日,把1582年月10月4日以后的一天改为10月15日,从中删去10天。
2、采用400年97闰法,即凡公元年号能被4整除为闰年,但公元年号为整百年时,须能被400整除者方为闰年,(如1600年、2000年)。其它为平年(如1700年、1900年)。
这就是目前世界上通用的阳历,又称“格列历”。至于岁首和纪元的设置,也是人为而定。现在的岁首是儒略·恺撒颁布历法时规定的,即定在冬至后十天为一月一日,因此有“冬至十天阳历年”的说法。古代欧洲和我国过去一样常采用“王位纪年法”,即将某个统治者登基作为纪年的开始,在西欧的罗马帝国则以罗马统治者狄奥·支列颠称帝时作为纪年的开始。后来有个叫狄奥尼亚的基督僧侣在预先推算狄奥支列颠纪元248年的“复活节”日期时,提出所谓耶稣诞生于狄奥·支列颠纪元前284年的说法,并主张以耶稣诞生的一年为纪元。它的主张竟然得到教会的大力支持,这样,狄奥支列颠248年就成为耶稣诞生纪年的532年。因此,现行的公历纪年,实际上从公元532年才在一些地区开始实行,到现在逐步成为全世界通用的正式纪年。
结论
由上面的表述可知道,现行历法是从1582年10月15日开始执行的,所以本文开头的算法只适用于计算1582年10月15日之后的日期。
按当前方法计算,1500年应是平年,但实际上那一年的二月还是29天。
1500年还没有施行现行历法呢,当然是不准的了。![]()
参考文献
- 行者 http://blog.csdn.net/liuyuan185442111
- Tomohiko Sakamoto 星期计算算法推导 http://blog.chinaunix.net/uid-24118190-id-75289.html
- 1582年10月5日是个很奇怪的日子 http://blog.csdn.net/sunxing007/article/details/5675342
- 公历和农历由来 历史上"丢失"的10天:1582年月10月5日至1582年月10月14日 http://bbs.csdn.net/topics/340135066
- 一五八二年十月四日是星期几 http://www.cnblogs.com/skyivben/archive/2010/06/14/1758056.html