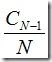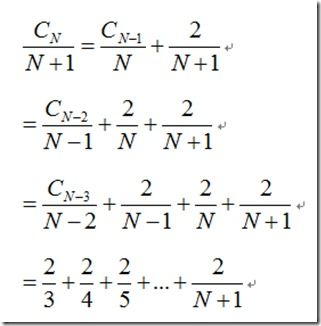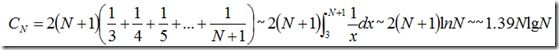快速排序
快速排序是20世纪科技领域的十大算法之一 ,他由C. A. R. Hoare于1960年提出的一种划分交换排序。
快速排序也是一种采用分治法解决问题的一个典型应用。在很多编程语言中,对数组,列表进行的非稳定排序在内部实现中都使用的是快速排序。而且快速排序在面试中经常会遇到。
本文首先介绍快速排序的思路,算法的实现、分析、优化及改进,最后分析了.NET 中列表排序的内部实现。
一 原理
快速排序的基本思想如下:
- 对数组进行随机化。
- 从数列中取出一个数作为中轴数(pivot)。
- 将比这个数大的数放到它的右边,小于或等于它的数放到它的左边。
- 再对左右区间重复第三步,直到各区间只有一个数。
如上图所示快速排序的一个重要步骤是对序列进行以中轴数进行划分,左边都小于这个中轴数,右边都大于该中轴数,然后对左右的子序列继续这一步骤直到子序列长度为1。
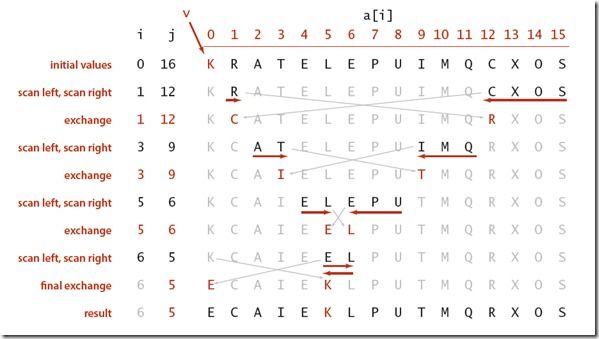
下面来看某一次划分的步骤,如下图:
上图中的划分操作可以分为以下5个步骤:
- 获取中轴元素
- i从左至右扫描,如果小于基准元素,则i自增,否则记下a[i]
- j从右至左扫描,如果大于基准元素,则i自减,否则记下a[j]
- 交换a[i]和a[j]
- 重复这一步骤直至i和j交错,然后和基准元素比较,然后交换。
划分过程的代码实现如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
/// <summary>
/// 快速排序中的划分过程
/// </summary>
/// <param name="array">待划分的数组</param>
/// <param name="lo">最左侧位置</param>
/// <param name="hi">最右侧位置</param>
/// <returns>中间元素位置</returns>
private
static
int
Partition(T[] array,
int
lo,
int
hi)
{
int
i = lo, j = hi +
1
;
while
(
true
)
{
//从左至右扫描,如果碰到比基准元素array[lo]小,则该元素已经位于正确的分区,i自增,继续比较i+1;
//否则,退出循环,准备交换
while
(array[++i].CompareTo(array[lo]) <
0
)
{
//如果扫描到了最右端,退出循环
if
(i == hi)
break
;
}
//从右自左扫描,如果碰到比基准元素array[lo]大,则该元素已经位于正确的分区,j自减,继续比较j-1
//否则,退出循环,准备交换
while
(array[--j].CompareTo(array[lo]) >
0
)
{
//如果扫描到了最左端,退出循环
if
(j == lo)
break
;
}
//如果相遇,退出循环
if
(i >= j)
break
;
//交换左a[i],a[j]右两个元素,交换完后他们都位于正确的分区
Swap(array, i, j);
}
//经过相遇后,最后一次a[i]和a[j]的交换
//a[j]比a[lo]小,a[i]比a[lo]大,所以将基准元素与a[j]交换
Swap(array, lo, j);
//返回扫描相遇的位置点
return
j;
}
|
划分前后,元素在序列中的分布如下图:
二 实现
与合并算法基于合并这一过程一样,快速排序基于分割(Partition)这一过程。只需要递归调用Partition这一操作,每一次以Partition返回的元素位置来划分为左右两个子序列,然后继续这一过程直到子序列长度为1,代码的实现如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public
class
QuickSort<T> where T : IComparable<T>
{
public
static
void
Sort(T[] array)
{
Sort(array,
0
, array.Length -
1
);
}
private
static
void
Sort(T[] array,
int
lo,
int
hi)
{
//如果子序列为1,则直接返回
if
(lo >= hi)
return
;
//划分,划分完成之后,分为左右序列,左边所有元素小于array[index],右边所有元素大于array[index]
int
index = Partition(array, lo, hi);
//对左右子序列进行排序完成之后,整个序列就有序了
//对左边序列进行递归排序
Sort(array, lo, index -
1
);
//对右边序列进行递归排序
Sort(array, index +
1
, hi);
}
}
|
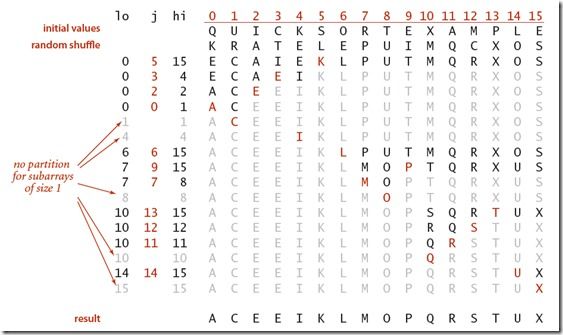
下图说明了快速排序中,每一次划分之后的结果:
一般快速排序的动画如下:
三 分析
- 在最好的情况下,快速排序只需要大约nlgn次比较操作,在最坏的情况下需要大约1/2 n2 次比较操作。在最好的情况下,每次的划分都会恰好从中间将序列划分开来,那么只需要lgn次划分即可划分完成,是一个标准的分治算法Cn=2Cn/2+N,每一次划分都需要比较N次,大家可以回想下我们是如何证明合并排序的时间复杂度的。
 在最坏的情况下,即序列已经排好序的情况下,每次划分都恰好把数组划分成了0,n两部分,那么需要n次划分,但是比较的次数则变成了n, n-1, n-2,….1, 所以整个比较次数约为n(n-1)/2~n2/2.
在最坏的情况下,即序列已经排好序的情况下,每次划分都恰好把数组划分成了0,n两部分,那么需要n次划分,但是比较的次数则变成了n, n-1, n-2,….1, 所以整个比较次数约为n(n-1)/2~n2/2. - 快速排序平均需要大约2NlnN次比较,来对长度为n的排序关键字唯一的序列进行排序。 证明也比较简单:假设CN为快速排序平均花在比较上的时间,初始C0=C1=0,对于N>1的情况,有:其中N+1是分割时的比较次数, 表示将序列分割为0,和N-1左右两部分的概率为1/N, 划分为1,N-2左右两部分的概率也为1/N,都是等概率的。然后对上式左右两边同时乘以N,整理得到:
然后,对于N为N-1的情况:
两式相减,然后整理得到:
然后左右两边同时除以N(N+1),得到:
然后处理一下得到:
- 平均情况下,快速排序需要大约1.39NlgN次比较,这比合并排序多了39%的比较,但是由于涉及了较少的数据交换和移动操作,他要比合并排序更快。
- 为了避免出现最坏的情况,导致序列划分不均,我们可以首先对序列进行随机化排列然后再进行排序就可以避免这一情况的出现。
- 快速排序是一种就地(in-place)排序算法。在分割操作中只需要常数个额外的空间。在递归中,也只需要对数个额外空间。
- 另外,快速排序是非稳定性排序。
四 改进
对一般快速排序进行一些改进可以提高其效率。
1. 当划分到较小的子序列时,通常可以使用插入排序替代快速排序
对于较小的子序列(通常序列元素个数为10个左右),我们就可以采用插入排序直接进行排序而不用继续递归,算法改造如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
private
const
int
CUTTOFF =
10
;
private
static
void
Sort(T[] array,
int
lo,
int
hi)
{
//如果子序列为1,则直接返回
if
(lo >= hi)
return
;
//对于小序列,直接采用插入排序替代
if
(hi - lo <= CUTTOFF -
1
)
{
Sort<
int
>.InsertionSort(array, lo, hi);
return
;
}
//划分,划分完成之后,分为左右序列,左边所有元素小于array[index],右边所有元素大于array[index]
int
index = Partition(array, lo, hi);
//对左右子序列进行排序完成之后,整个序列就有序了
//对左边序列进行递归排序
Sort(array, lo, index -
1
);
//对右边序列进行递归排序
Sort(array, index +
1
, hi);
}
|
2. 三平均分区法(Median of three partitioning)
在一般的的快速排序中,选择的是第一个元素作为中轴(pivot),这会出现某些分区严重不均的极端情况,比如划分为了1和n-1两个序列,从而导致出现最坏的情况。三平均分区法与一般的快速排序方法不同,它并不是选择待排数组的第一个数作为中轴,而是选用待排数组最左边、最右边和最中间的三个元素的中间值作为中轴。这一改进对于原来的快速排序算法来说,主要有两点优势:
(1) 首先,它使得最坏情况发生的几率减小了。
(2) 其次,未改进的快速排序算法为了防止比较时数组越界,在最后要设置一个哨点。如果在分区排序时,中间的这个元素(也即中轴)是与最右边数过来第二个元素进行交换的话,那么就可以省略与这一哨点值的比较。
对于三平均分区法还可以进一步扩展,在选取中轴值时,可以从由左中右三个中选取扩大到五个元素中或者更多元素中选取,一般的,会有(2t+1)平均分区法(median-of-(2t+1)。常用的一个改进是,当序列元素小于某个阈值N时,采用三平均分区,当大于时采用5平均分区。
采用三平均分区法对快速排序的改进如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
private
static
void
Sort(T[] array,
int
lo,
int
hi)
{
//对于小序列,直接采用插入排序替代
if
(hi - lo <= CUTTOFF -
1
)
{
//Sort<int>.InsertionSort(array, lo, hi);
return
;
}
//采用三平均分区法查找中轴
int
m = MedianOf3(array, lo, lo + (hi - lo) /
2
, hi);
Swap(array, lo, m);
//划分,划分完成之后,分为左右序列,左边所有元素小于array[index],右边所有元素大于array[index]
int
index = Partition(array, lo, hi);
//对左右子序列进行排序完成之后,整个序列就有序了
//对左边序列进行递归排序
Sort(array, lo, index -
1
);
//对右边序列进行递归排序
Sort(array, index +
1
, hi);
}
/// <summary>
/// 查找三个元素中位于中间的那个元素
/// </summary>
/// <param name="array"></param>
/// <param name="lo"></param>
/// <param name="center"></param>
/// <param name="hi"></param>
/// <returns></returns>
private
static
int
MedianOf3(T[] array,
int
lo,
int
center,
int
hi)
{
return
(Less(array[lo], array[center]) ?
(Less(array[center], array[hi]) ? center : Less(array[lo], array[hi]) ? hi : lo) :
(Less(array[hi], array[center]) ? center : Less(array[hi], array[lo]) ? hi : lo));
}
private
static
bool Less(T t1, T t2)
{
return
t1.CompareTo(t2) <
0
;
}
|
使用插入排序对小序列进行排序以及使用三平均分区法对一般快速排序进行改进后运行结果示意图如下:
3. 三分区(3-way partitioning) 快速排序
通常,我们的待排序的序列关键字中会有很多重复的值,比如我们想对所有的学生按照年龄进行排序,按照性别进行排序等,这样每一类别中会有很多的重复的值。理论上,这些重复的值只需要处理一次就行了。但是一般的快速排序会递归进行划分,因为一般的快速排序只是将序列划分为了两部分,小于或者大于等于这两部分。
既然要利用连续、相等的元素不需要再参与排序这个事实,一个直接的想法就是通过划分让相等的元素连续地摆放:
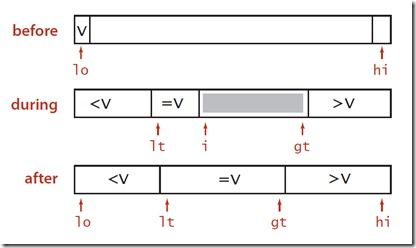
然后只对左侧小于V的序列和右侧大于V对的序列进行排序。这种三路划分与计算机科学中无处不在,它与Dijkstra提出的“荷兰国旗问题”(The Dutch National Flag Problem)非常相似。
Dijkstra的方法如上图:
从左至右扫描数组,维护一个指针lt使得[lo…lt-1]中的元素都比v小,一个指针gt使得所有[gt+1….hi]的元素都大于v,以及一个指针i,使得所有[lt…i-1]的元素都和v相等。元素[i…gt]之间是还没有处理到的元素,i从lo开始,从左至右开始扫描:
· 如果a[i]<v: 交换a[lt]和a[i],lt和i自增
· 如果a[i]>v:交换a[i]和a[gt], gt自减
· 如果a[i]=v: i自增
下面是使用Dijkstra的三分区快速排序代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
private
static
void
Sort(T[] array,
int
lo,
int
hi)
{
//对于小序列,直接采用插入排序替代
if
(hi - lo <= CUTTOFF -
1
)
{
Sort<
int
>.InsertionSort(array, lo, hi);
return
;
}
//三分区
int
lt = lo, i = lo +
1
, gt = hi;
T v = array[lo];
while
(i<=gt)
{
int
cmp = array[i].CompareTo(v);
if
(cmp <
0
) Swap(array, lt++, i++);
else
if
(cmp >
0
) Swap(array, i, gt--);
else
i++;
}
//对左边序列进行递归排序
Sort(array, lo, lt -
1
);
//对右边序列进行递归排序
Sort(array, gt +
1
, hi);
}
|
三分区快速排序的每一步如下图所示:
三分区快速排序的示意图如下:
Dijkstra的三分区快速排序虽然在快速排序发现不久后就提出来了,但是对于序列中重复值不多的情况下,它比传统的2分区快速排序需要更多的交换次数。
Bentley 和D. McIlroy在普通的三分区快速排序的基础上,对一般的快速排序进行了改进。在划分过程中,i遇到的与v相等的元素交换到最左边,j遇到的与v相等的元素交换到最右边,i与j相遇后再把数组两端与v相等的元素交换到中间
这个方法不能完全满足只扫描一次的要求,但它有两个好处:首先,如果数据中没有重复的值,那么该方法几乎没有额外的开销;其次,如果有重复值,那么这些重复的值不会参与下一趟排序,减少了无用的划分。
下面是采用 Bentley&D. McIlroy 三分区快速排序的算法改进:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
private
static
void
Sort(T[] array,
int
lo,
int
hi)
{
//对于小序列,直接采用插入排序替代
if
(hi - lo <= CUTTOFF -
1
)
{
Sort<
int
>.InsertionSort(array, lo, hi);
return
;
}
// Bentley-McIlroy 3-way partitioning
int
i = lo, j = hi +
1
;
int
p = lo, q = hi +
1
;
T v = array[lo];
while
(
true
)
{
while
(Less(array[++i], v))
if
(i == hi)
break
;
while
(Less(v, array[--j]))
if
(j == lo)
break
;
// pointers cross
if
(i == j && Equal(array[i], v))
Swap(array, ++p, i);
if
(i >= j)
break
;
Swap(array, i, j);
if
(Equal(array[i], v)) Swap(array, ++p, i);
if
(Equal(array[j], v)) Swap(array, --q, j);
}
//将相等的元素交换到中间
i = j +
1
;
for
(
int
k = lo; k <= p; k++) Swap(array, k, j--);
for
(
int
k = hi; k >= q; k--) Swap(array, k, i++);
Sort(array, lo, j);
Sort(array, i, hi);
}
|
三分区快速排序的动画如下:
4.并行化
和前面讨论对合并排序的改进一样,对所有使用分治法解决问题的算法其实都可以进行并行化,快速排序的并行化改进我在之前的浅谈并发与并行这篇文章中已经有过介绍,这里不再赘述。
五 .NET 中元素排序的内部实现
快速排序作为一种优秀的排序算法,在很多编程语言的元素内部排序中均有实现,比如Java中对基本数据类型(primitive type)的排序,C++,Matlab,Python,FireFox Javascript等语言中均将快速排序作为其内部元素排序的算法。同样.NET中亦是如此。
.NET这种对List<T>数组元素进行排序是通过调用Sort方法实现的,其内部则又是通过Array.Sort实现,MSDN上说在.NET 4.0及之前的版本,Array.Sort采用的是快速排序,然而在.NET 4.5中,则对这一算法进行了改进,采用了名为Introspective sort 的算法,即保证在一般情况下达到最快排序速度,又能保证能够在出现最差情况是进行优化。他其实是一种混合算法:
- 当待分区的元素个数小于16个时,采用插入排序
- 当分区次数超过2*logN,N是输入数组的区间大小,则使用堆排序(Heapsort)
- 否则,使用快速排序。
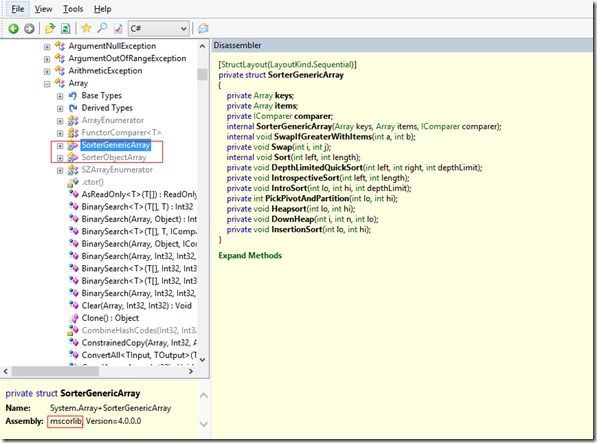
有了Reflector这一神器,我们可以查看.NET中的ArraySort的具体实现:
Array.Sort这一方法在mscorlib这一程序集中,具体的实现方法有分别针对泛型和普通类型的SortedGenericArray和SortedObjectArray,里面的实现大同小异,我们以SortedGenericArray这个类来作为例子看:
首先要看的是Sort方法,其实现如下:
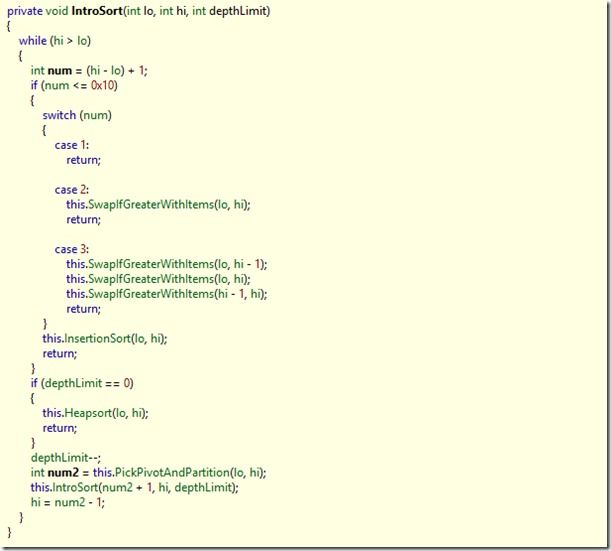
该方法中,首先判断运行的.NET对的版本,如果是4.5及以上版本,则用IntrospectiveSort算法,否则采用限定深度的快速排序算法DepthLimitedQuickSort。先看IntrospectiveSort:
该方法第一个元素为数组的最左边元素位置,第二个参数为最右边元素位置,第三个参数为2*log2N,继续看方法内部:
可以看到,当num<=16时,如果元素个数为1,2,3,则直接调用SwapIfGreaterWithItem进行排序了。否则直接调用InsertSort进行插入排序。
这里面也是一个循环,每循环一下depthLimit就减小1个,如果为0表示划分的次数超过了2logN,则直接调用基排序(HeapSort),这里面的划分方法PickPivortAndPartitin的实现如下:
它其实是一个标准的三平均快速排序。可以看到在.NET 4.5中对Quick进行优化的部分主要是在元素个数比较少的时候采用选择插入,并且在递归深度超过2logN的时候,采用基排序。
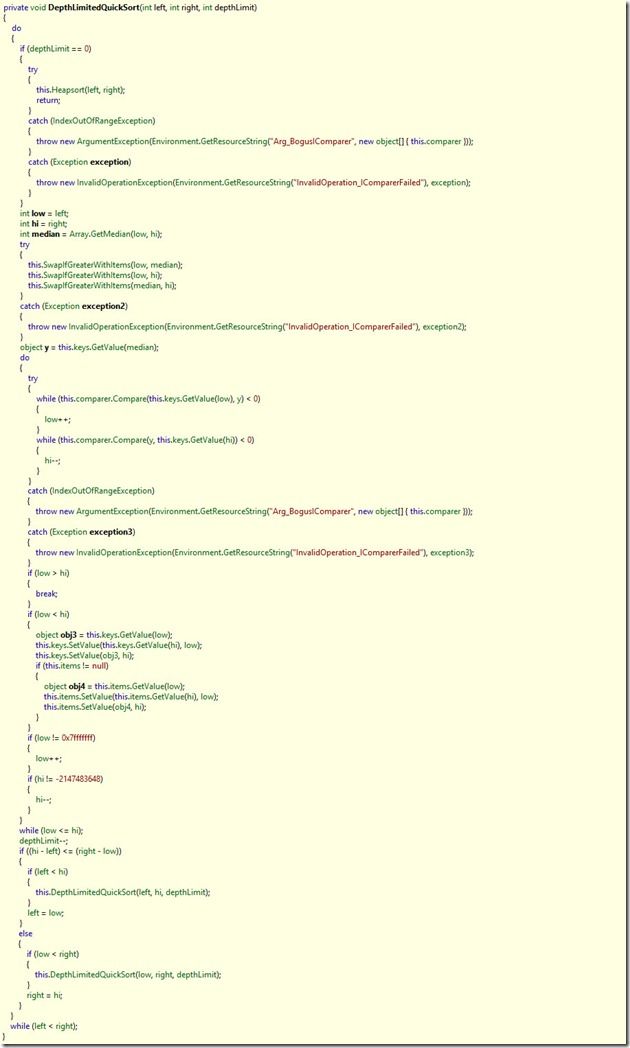
下面再来看下在.NET 4.0及以下平台下排序DepthLimitedQuickSort方法的实现:
从名称中可以看出这是限定深度的快速排序,在第三个参数传进去的是0×20,也就是32。
可以看到,当划分的次数大于固定的32次的时候,采用了基排序,其他的部分是普通的快速排序。
六 总结
由于快速排序在排序算法中具有排序速度快,而且是就地排序等优点,使得在许多编程语言的内部元素排序实现中采用的就是快速排序,本问首先介绍了一般的快速排序,分析了快速排序的时间复杂度,然后就分析了对快速排序的几点改进,包括对小序列采用插入排序替代,三平均划分,三分区划分等改进方法。最后介绍了.NET不同版本下的对元素内部排序的实现。