排序算法之 基数排序 及其时间复杂度和空间复杂度

        基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

算法分析

     主要思想：

        基数排序的实现虽然有很多，但是基本思想就是把元素从个位排好序，然后再从十位排好序，，，，一直到元素中最大数的最高位排好序，那么整个元素就排好序了。

                比如：2，22，31，1221，90，85，105

        个位排序：90，31，1221，2，22，85，105

        十位排序：2，105，1221，22，31，85，90

        百位排序：2，22，31，85，90，105，1221

        千位排序：2，22，31，85，90，105，1221

         注意：每次排序都是在上次排序的基础上进行排序的，也就是说此次排序的位数上他们相对时，就不移动元素（即顺序参数上一个位数的排序顺序）

    主要步骤：

        1、把所有元素都分配到相应的桶中

       2、把所有桶中的元素都集合起来放回到数组中

       3、依次循环上面两步，循环次数为最大元素最高位数

    代码分析：

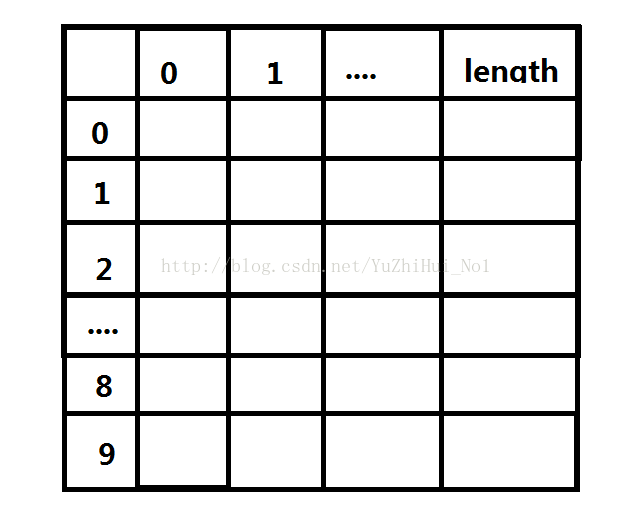
        参考下图

     1、竖  0～9：表示桶个数（每个位数上的数字都在0到9之间）；

     2、行 0～length：0 表示在某个桶内有多少个元素；

     3、比如：所有元素中个位为5的有两个元素，5 ， 95；那么在下图中存放，分别是：（5，0） = 2；（5，1） = 5；（5，2）= 95；

代码实现

 #include<stdio.h>
 #include<stdlib.h>
 
 #define LEN 10
                          
 // 打印数组元素
 void print_array(int *array, int length)
 {
     int index = 0;
     printf("array:\n");
     for(; index < length; index++){
         printf(" %d,", *(array+index));
     }
     printf("\n\n");
 }
 
// 得到数组元素中最大数，并且计算其位数个数
 void getPosCount(int *array, int length, int *posCount)
 {
     int max, index;
     for (max = *array, index = 0; index < length; index++){
         if ( max < *(array + index)) max = *(array + index);
     }
 
     *posCount = 0;
     while(max){
         max = max / 10;
         (*posCount)++;
     }
 }
                          
void radixSort(int *array, int length)
 {
     int* tmpArray[LEN];// 定义桶个数 0～9 共10个
     int index, pos, posCount, element, elementNum, tmp, log = 1;  
 
     for (element = 0; element < LEN; element++){// 每个桶最大能装length个元素，预防所有元素都是同一个数
         tmpArray[element] = (int*)malloc((sizeof(int))*(length + 1));
         tmpArray[element][0] = 0;// 初始化为0
     }
 
     getPosCount(array, length, &posCount);// 把最高位数存放到posCount中
 
     for (pos = 0; pos < posCount; pos++){// 从个位 ～ 十位 ～ 百位 。。。依次排序
 
         for (element = 0; element < length; element++){// 把元素放到桶里  分配动作
             tmp = ++tmpArray[ (array[element] / log ) % 10][0];
             tmpArray[ (array[element] / log) % 10][tmp] = array[element];
         }
 
         for (index = 0, element = 0; (element < LEN) && (index < length); element++){
             for (elementNum = 1; elementNum <= tmpArray[element][0]; elementNum++)
                 array[index++] = tmpArray[element][elementNum];
             tmpArray[element][0] = 0;
         }
         log = log * 10;
     }
 }
                          
 int main(void)
 {
     int array[] = {2,  5, 337, 24, 10000, 5, 30, 123, 3, 9, 100, 1};
     //int array[] = {2,  5, 3, 4, 1, 5, 0, 2, 3, 9, 1, 7, 8, 6};
     //int array[] = {2,  5, 3, 4, 1, 5, 5, 55555, 9, 5, 7, 5, 6};
     int length = (sizeof(array)) / (sizeof(array[1]));
     print_array(array, length);
     radixSort(array, length);
     print_array(array, length);
 
     return 0;
 }

        运行结果：

        

时间复杂度

        该算法所花的时间基本是在把元素分配到桶里和把元素从桶里串起来；把元素分配到桶里：循环 length 次；

       把元素从桶里串起来：这个计算有点麻烦，看似两个循环，其实第二循环是根据桶里面的元素而定的，可以表示为：k×buckerCount；其中 k 表示某个桶中的元素个数，buckerCount  则表示存放元素的桶个数；

       有几种特殊情况：

       第一、所有的元素都存放在一个桶内：k = length，buckerCount = 1；

       第二、所有的元素平均分配到每个桶中：k = length/ bukerCount，buckerCount = 10；（这里已经固定了10个桶）

       所以平均情况下收集部分所花的时间为：length （也就是元素长度 n）

       综上所述：

       时间复杂度为：posCount * (length  + length) ；其中 posCount 为数组中最大元素的最高位数；简化下得：O( k*n ) ；其中k为常数，n为元素个数；

空间复杂度

        该算法的空间复杂度就是在分配元素时，使用的桶空间；所以空间复杂度为：O（10 × length）= O （length）

计数法基数排序

     主要思想：

        因为基数排序是根据个位是排序好，然后再根据十位数排序好，依次类推，当最后一个位数排序好时，所有的元素顺序都排序好了。又根据计数排序的算法可以得知，在限制元素的情况下，可以知道计数排序的时间复杂度为  O（n）；所有如果利用计数排序的原理的实现基数排序，那么时间复杂度是不是可以降低呢？

         注意：如果不知道计数排序的，可以先大概了解下：http://blog.csdn.net/yuzhihui_no1/article/details/44561487

代码实现

#include<stdio.h>
#include<stdlib.h>
 
 void print_array(int *array, int length)
 {
     int index = 0;
     printf("array:\n");
     for(; index < length; index++){
         printf(" %d,", *(array+index));
     }
     printf("\n\n");
 }

 void getCount(int *array, int length, int *count)
 {
     int max, index;

     for (max = *array, index = 0; index < length; index++){
         if ( max < *(array + index)) max = *(array + index);
     }
 
     *count = 0;
     while(max){
         max = max / 10;
         (*count)++;
     }
 }
 
 void radixSort(int *array, int length)
 {
     int *tmpArray = (int*)malloc(sizeof(int)*(10));
     int tmp[length];
     int i, j, count, log = 1;
 
     getCount(array, length, &count);
     for (j = 0; j < count; j++){ // 循环最大位数次
 
         for (i = 0; i < 10; i++)tmpArray[i] = 0;// 初始化数组
 
         for (i = 0; i < length; i++) tmpArray[ (array[i] / log) % 10 ]++;// 元素值对应桶标记
 
         for (i = 1; i <= 10; i++) tmpArray[i] += tmpArray[i-1];// 统计大于各元素的个数
 
         for (i = length - 1; i >= 0; i--){ // 按照指定位数对元素进行排序
             tmp[tmpArray[ (array[i] / log) % 10] - 1] = array[i];
             tmpArray[ (array[i] / log) % 10 ]--;
         }
 
         for (i = 0; i < length; i++) array[i] = tmp[i];// 把排序好的元素放回到元素数组中
         log = log * 10;
     }
 
     free(tmpArray);// 释放内存
 }
 
 int main(void)
 {
     //int array[] = {2,  5, 337, 24, 10000, 5, 30, 123, 3, 9, 100, 1};
     int array[] = {2,  5, 3, 4, 1, 5, 0, 2, 3, 9, 1, 7, 8, 6};
     int length = (sizeof(array)) / (sizeof(array[1]));
     print_array(array, length);
     radixSort(array, length);
     print_array(array, length);
 
     return 0;
 }

        运行结果：

        

时间复杂度

        这个时间复杂度比较好计算：count * length；其中 count 为数组元素最高位数，length为元素个数；所以时间复杂度：O（ k*n ）

空间复杂度

        空间复杂度是使用了两个临时的数组：10 + length；所以空间复杂度：O（n）

        转载请注明作者和原文出处，原文地址：http://blog.csdn.net/yuzhihui_no1/article/details/44594415

        若有不正确之处，望大家指正，共同学习！谢谢！！！