用Geogebra绘制一种五角星形曲线

实际上类似的曲线可以做很多，参考Benice的博客（或者此处上一篇博客转发的少量图片），但是这个五角星形状的曲线比较简单。

我从来只是把网络上BBS或博客之类的写的东西当作一种消遣而不是研究，所以，不能指望对文字内容从语法上严格推敲，除非很有兴趣也不太可能过问对我来说太艰涩繁复又非自己必须做的事情。——除非有合法而可观的佣金

圆圆相切的情况下谋点运动轨迹的描述，通过调整参数可以作出各种曲线，如果仔细研究，比如benice那样详细的总结，专门发一篇华丽丽的中文核心论文也没太大问题，但是我对发这种论文不感兴趣。

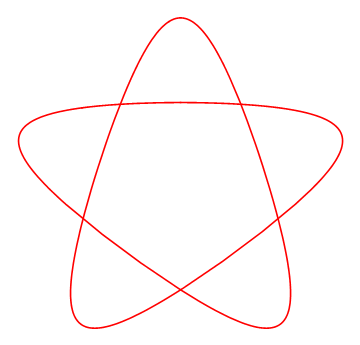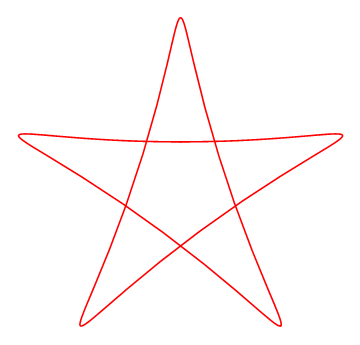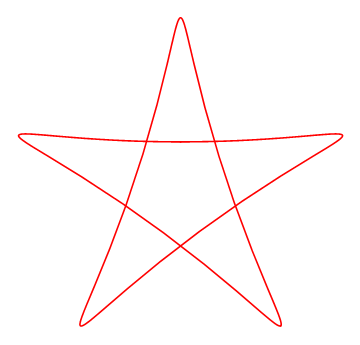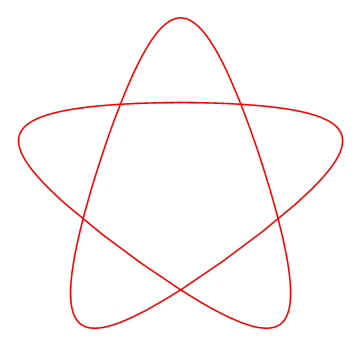
我只说说自己是怎么用Geogebra绘制出下面这条五角星形曲线的；为了网络上交流方便，这也是动机之一，还作成GIF动画的形式。

实际上在知道曲线参数方程之前是需要尝试的，这就是为什么说Matlab虽然强大，远不如geogebra方便的原因。术业有专攻。

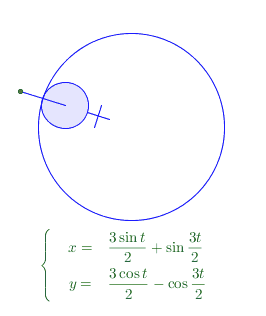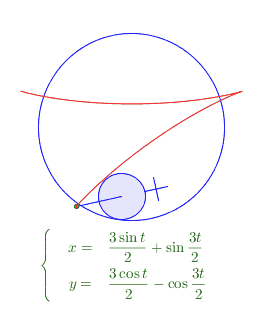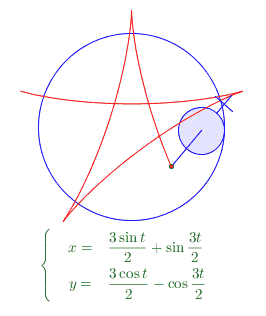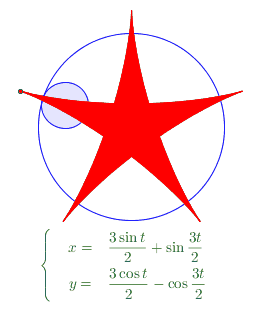
得到这样的五角星曲线纯属偶然，我先绘制一个以O=(0,0)为圆心半径为2的蓝色圆；然后以A=(1.5,0)为圆心绘制一个半径0.5的圆。这就是两个将要发生摩擦的圆。这个时候，我还不知道自己能画出什么曲线。考虑到小圆的圆心是运动的，所以，实际上(1.5,0)只是初始状态的值，我建立了一个geogebra中以角度为单位的slider变量，比如叫他alpha,或t,然它初值为0， A=1.5*(cos[t],sin[t]) 才是A的真实的坐标参数。

最初想要表达一个圆的滚动，我是用给圆增加一系列辐条的方式来实现，但是对照之下，发现benice的给圆增加一个“把”的方式视觉效果要好得多。所以就欣然借鉴了。

这个绘制是很简单的。增加这样的一个“把”是简单的操作。关键在于，这个把看上去似乎是总跟OA共线的，实际上运动起来发现，如果它总是跟OA共线，则运动轨迹总是圆！！ 所以，这个“把”在A点运动（或slider的值变化）的同时，相对于当前t时刻的OA还在发生旋转。 ——也就是小圆A在大圆O内侧滚动的同时，还在自旋，有相对滑动。我假设这个滑动的角速度是 n*t (n为有理数）。 结果发现，n=5/2的时候得到的就是上图的五角星形状的曲线。

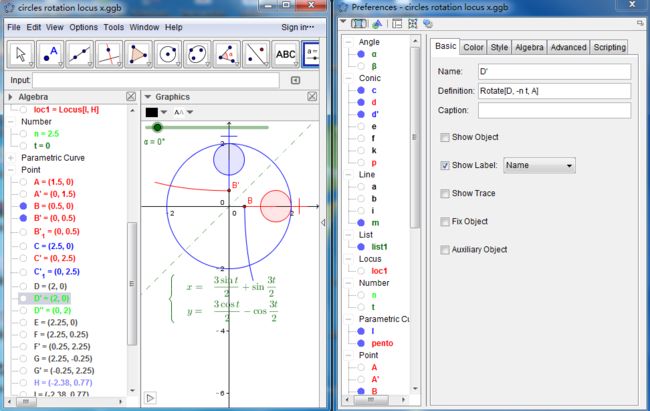
下面是制作的ggb文件的截图，希望对同样使用Geogebra的初学者有帮助：

这个时候已经知道的五角星形状的曲线是怎么来的了，但Geogebra还不能太容易得到它的最简单的参数方程，好了，把这项光荣而艰巨的任务交给Mathematica好了（选好工具选对人）

于是参数方程很容易就求出来了。如图所示。

很容易发现第二项的系数决定着五角星的"肥瘦程度"

Manipulate[
 ParametricPlot[{3 Sin[t]/2 + a Sin[3 t/2], 
   3 Cos[t]/2 - a Cos[3 t/2]}, {t, 0, 4 Pi}, PlotStyle -> Red, 
  Axes -> False], {a, 1/2, 1}]

它要变成一朵花也没办法:

Manipulate[
 ParametricPlot[{ Sin[t] + a Sin[3 t/2], Cos[t] - a Cos[3 t/2]}, {t,    0, 4 Pi}, PlotStyle -> Red, Axes -> False], {a, 1/3, 1}]