推荐系统(一):频繁模式挖掘的FPGrowth实现
算法说明:FPGrowth算法是用来做购物车分析,说白了就是分析下什么商品和什么商品会被一同购买,还有一同购买的频次是多少,经常被一同购买的商品就可以放到一起做推荐了。
频繁模式挖掘关键词说明:
挖掘数据机:购物篮数据
频繁模式:频繁出现在数据集当中的模式:项集、子结构、子序列
挖掘目标:频繁项集,频繁模式,关联规则
关联规则:牛奶=>鸡蛋,[支持度=2%,置信度=60%]
支持度:%2的购物车买了牛奶也买了鸡蛋,可用百分比也可用具体数字
置信度:60%购买了牛奶的人同时买了鸡蛋
最小支持度:支持度阀值
项集:商品集合
K-项集:K个商品组成的集合
频繁项集:满足最小支持度的项集
下面我们来看下如何通过FPGrowth算法来进行频繁模式挖掘:
1.我们要有一个购物车数据集
I1,I2,I4 I1,I2,I5 I2,I4 I2,I3 I1,I3 I2,I3 I1,I3 I1,I2,I3,I5 I1,I2,I3
2.定一个最小支持度计数,我们暂定为2。
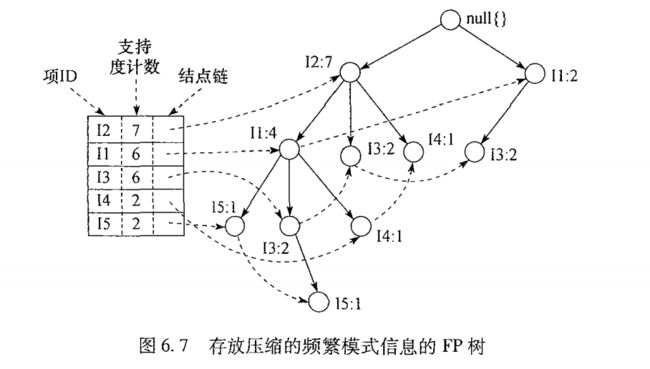
3.下面我们要建立FPTree,FP树是对购物车数据集的一个重构,也是我们FPGrowth算法的基础。我们从韩家炜的书中,摘取出一副FPTree的构造图,然后来分析一下这棵树是如何建立的。首先对购物车的所有商品按支持度计数(在购物车中出线几次)排序,同时放弃支持度计数小于最小支持度计数的项,形成频繁项头链表。以频繁项头链表为基准,扫描每条购物车信息,排序并删除支持度计数过小的项。先建立null结点(FPTree根节点),读入一条购物车信息,按顺序建立树形结构,如果结点已存在直接增加该结点的支持度计数。同时在建立新结点的时候把该结点加入到频繁项头链表的结点链中。
先来定义一下数据结构:
//购物车项信息:itemName为商品名称,supportCount为购物车中的商品数量
case class Item(val itemName: String, var supportCount: Int)
//FP树结点:nodeName为商品名称
class FPTreeNode(val nodeName: String) {
var supportCount: Int = 0 //支持度计数
var parent: Option[FPTreeNode] = None //父结点
var children: mutable.Map[String, FPTreeNode] = mutable.Map() //孩子结点
def increaseSupportCount(n: Int) = supportCount += n //增加支持度计数
def isLeaf = if (children.size == 0) true else false //是否为叶子结点
}
//FP树结构
class FPTree(val name: String, val frequencyItems: List[FrequencyItem]) {
//根节点
val root = new FPTreeNode(name)
//记录当前递归结点
var currentNode = root
def resumeCurrentNode {
currentNode = root
}
/**
* 判断当前FPTree是一棵单叉树
*
* @return
*/
def isSingleTree: Boolean = {
var treeNode = root
while (!treeNode.isLeaf) {
if (treeNode.children.size == 1) {
treeNode = treeNode.children.head._2
} else {
return false
}
}
return true
}
//空树
def isNullTree: Boolean = {
if (root.children.size == 0) return true
else return false
}
}
//频繁项集头列表
class FrequencyItem(val itemName: String, val supportCount: Int) {
val treeNodes: mutable.ArrayBuffer[FPTreeNode] = mutable.ArrayBuffer()
}
首先扫描一遍购物车,构建frequencyItemIndex,用来对频繁项安支持度计数排序Map(频繁项,序号),序号小的靠前
val frequencyItemIndex = mutable.LinkedHashMap[String, Int]()
扫描购物车并建立FPTree
/**
* 扫描购物车 生成FPTree
*
* @param fileName
* @return
*/
def scanCartList(fileName: String): FPTree = {
val itemsList = mutable.ListBuffer[List[Item]]()
//第一次扫描购物车购物车
for (line <- Source.fromFile(fileName).getLines()) {
//分别统计每哥购物车的频繁项支持度和所有购物车频繁项支持度
val cartItemMap = collection.mutable.Map[String, Int]()
for (itemName <- line.split(",")) {
cartItemMap.get(itemName) match {
case Some(_supportCount) => cartItemMap.put(itemName, _supportCount + 1)
case None => cartItemMap += (itemName -> 1)
}
frequencyItemIndex.get(itemName) match {
case Some(_supportCount) => frequencyItemIndex.put(itemName, _supportCount + 1)
case None => frequencyItemIndex += (itemName -> 1)
}
}
itemsList += (for (cartItem <- cartItemMap.toList) yield new Item(cartItem._1, cartItem._2))
}
//移除支持度计数过小的频繁项
frequencyItemIndex.foreach(x => {
if (x._2 < minSupportCount) frequencyItemIndex -= x._1
})
//生成频繁项头链表
val frequencyItemHeadList = frequencyItemIndex
.toList
.sortWith((x, y) => x._2 > y._2)
.map(x => new FrequencyItem(x._1, x._2))
println("开是构建FPTree...")
print("\t打印频繁模式项头:")
frequencyItemHeadList.foreach(x => printf("%s:%d ", x.itemName, x.supportCount))
println("")
val fpTree = new FPTree("root", frequencyItemHeadList.toList)
for (i <- 0 until frequencyItemHeadList.size) {
frequencyItemIndex.put(frequencyItemHeadList(i).itemName, i)
}
for (items <- itemsList) {
val _items = items
.filter(item => frequencyItemIndex.isDefinedAt(item.itemName))
.sortWith((x, y) => frequencyItemIndex(x.itemName) < frequencyItemIndex(y.itemName))
print("\t扫描频繁项集合:")
_items.foreach(x => printf("%s:%d ", x.itemName, x.supportCount))
println("")
insertTree(_items, fpTree)
fpTree.resumeCurrentNode
}
fpTree
}
递归建树方法:
/**
* 插入构建FP树
*
* @param items 购物篮信息(频繁模式项集)
* @param fPTree FP树
*/
def insertTree(items: List[Item], fPTree: FPTree) {
for (item <- items) {
fPTree.currentNode.children.get(item.itemName) match {
case Some(child) => {
child.increaseSupportCount(item.supportCount)
printf("\t\t增加支持度计数:%s up to %d\n", child.nodeName, child.supportCount)
}
case None => {
val child = new FPTreeNode(item.itemName)
child.increaseSupportCount(item.supportCount)
child.parent = Some(fPTree.currentNode)
fPTree.currentNode.children += (child.nodeName -> child)
printf("\t\t在%s下面增加新结点%s:%d\n", fPTree.currentNode.nodeName, child.nodeName, child.supportCount)
fPTree.frequencyItems.find(x => x.itemName == child.nodeName) match {
case Some(frequencyItem) => {
frequencyItem.treeNodes += child
printf("\t\t\t把新结点%s:%d,加入频繁模式头链表\n", child.nodeName, child.supportCount)
}
case None => println("[ERROR]:丢失频繁模式项头信息!!!!!!!!")
}
}
}
fPTree.currentNode = fPTree.currentNode.children(item.itemName)
}
}
看下打印的建树信息
开是构建FPTree... 打印频繁模式项头:I2:7 I1:6 I3:6 I4:2 I5:2 扫描频繁项集合:I2:1 I1:1 I4:1 在root下面增加新结点I2:1 把新结点I2:1,加入频繁模式头链表 在I2下面增加新结点I1:1 把新结点I1:1,加入频繁模式头链表 在I1下面增加新结点I4:1 把新结点I4:1,加入频繁模式头链表 扫描频繁项集合:I2:1 I1:1 I5:1 增加支持度计数:I2 up to 2 增加支持度计数:I1 up to 2 在I1下面增加新结点I5:1 把新结点I5:1,加入频繁模式头链表 扫描频繁项集合:I2:1 I4:1 增加支持度计数:I2 up to 3 在I2下面增加新结点I4:1 把新结点I4:1,加入频繁模式头链表 扫描频繁项集合:I2:1 I3:1 增加支持度计数:I2 up to 4 在I2下面增加新结点I3:1 把新结点I3:1,加入频繁模式头链表 扫描频繁项集合:I1:1 I3:1 在root下面增加新结点I1:1 把新结点I1:1,加入频繁模式头链表 在I1下面增加新结点I3:1 把新结点I3:1,加入频繁模式头链表 扫描频繁项集合:I2:1 I3:1 增加支持度计数:I2 up to 5 增加支持度计数:I3 up to 2 扫描频繁项集合:I1:1 I3:1 增加支持度计数:I1 up to 2 增加支持度计数:I3 up to 2 扫描频繁项集合:I2:1 I1:1 I3:1 I5:1 增加支持度计数:I2 up to 6 增加支持度计数:I1 up to 3 在I1下面增加新结点I3:1 把新结点I3:1,加入频繁模式头链表 在I3下面增加新结点I5:1 把新结点I5:1,加入频繁模式头链表 扫描频繁项集合:I2:1 I1:1 I3:1 增加支持度计数:I2 up to 7 增加支持度计数:I1 up to 4 增加支持度计数:I3 up to 2
建树完毕,开始挖掘,这次是今天我重点要说的,先来看下书上给出的算法:
实在是没办法按这个写出来代码,这只能算是一个指导方向,我来重写一份看看
FP_growth(FP_tree, _CPI) (1)if FP_tree 只有一条路径P && _CPI不空 (2)for b <- p的所有组合 (3)产生频繁模式bp,support_count=bp中最小的support_count (4)else for frequencyItem <- FP_tree的频繁项头链表.逆序 (5)if frequencyItem 的结点链只有一个结点 && _CPI不空 (6)for b <- frequencyItem.结点开始上溯到根结点组成的路径P (7)产生频繁模式bp,support_count=bp中最小的support_count (8)else frequencyItem 的结点链只有多个结点 (9)for p <- frequencyItem.结点链 (10)根据P路径构造条件模式基集合_CPBs (11)使用_CPBs建立FP树_FP_tree (12)if _FP_tree != null (13)frequencyItem并上_CPI,support_count=frequencyItem.support_count (14)if _CPI 不为空 生成频繁模式 frequencyItem_CPI:frequencyItem.support_count (15)FP_growth(_FP_tree, frequencyItem_CPI:frequencyItem.support_count)
/**
* 挖掘频繁模式
*
* @param fPTree FPTree: FP树 CPTree:条件模式树
* @param _CPI 条件模式项
*/
def fp_growth(fPTree: FPTree, _CPI: Option[Item]): Unit = {
if (fPTree.isSingleTree && _CPI != None) {
_CPI match {
case Some(cpItem) => {
val _CPB = fPTree.frequencyItems.map(x => Item(x.itemName, x.supportCount))
if (_CPB.size > 0) {
println()
printf("挖掘%s:%d的频繁模式:", _CPI.get.itemName, _CPI.get.supportCount)
generateFrequencyPattern(_CPB, cpItem)
println()
}
}
case None => {
}
}
} else {
fPTree.frequencyItems.reverse.foreach(frequencyItem => {
if (frequencyItem.treeNodes.size == 1 && _CPI != None) {
val _CPB = mutable.ListBuffer[Item]()
val treeNode = frequencyItem.treeNodes(0)
_CPB += Item(treeNode.nodeName, treeNode.supportCount)
var parentNode = treeNode.parent
while (parentNode != None && parentNode.get.nodeName != "root") {
_CPB += Item(parentNode.get.nodeName, treeNode.supportCount)
parentNode = parentNode.get.parent
}
println()
printf("挖掘%s:%d的频繁模式:", _CPI.get.itemName, _CPI.get.supportCount)
if (_CPB.size > 0) {
generateFrequencyPattern(_CPB.toList, _CPI.get)
println()
}
} else {
var itemName = frequencyItem.itemName
if (_CPI != None) {
itemName = itemName + "," + _CPI.get.itemName
printf("挖掘%s:%d的频繁模式:{%s:%d}", _CPI.get.itemName, _CPI.get.supportCount, itemName, frequencyItem.supportCount)
}
println()
printf("建立%s:%d的条件模式树:\n", itemName, frequencyItem.supportCount)
val _fpTree = buileConditionPatternFree(frequencyItem)
if (!fPTree.isNullTree) fp_growth(_fpTree, Some(Item(itemName, frequencyItem.supportCount)))
}
})
}
/**
* 构造条件模式树
*
* @param frequencyItem
* @return
*/
def buileConditionPatternFree (frequencyItem: FrequencyItem): FPTree = {
val _CPBs = mutable.ListBuffer[List[Item]]()
val frequencyItemMap = mutable.Map[String, Int]()
for (treeNode <- frequencyItem.treeNodes) {
val _CPB = mutable.ListBuffer[Item]()
var parentNode = treeNode.parent
while (parentNode != None && parentNode.get.nodeName != "root") {
val item = Item(parentNode.get.nodeName, treeNode.supportCount)
frequencyItemMap.get(item.itemName) match {
case Some(supportCount) => frequencyItemMap.put(item.itemName, supportCount + item.supportCount)
case None => frequencyItemMap += (item.itemName -> item.supportCount)
}
_CPB += item
parentNode = parentNode.get.parent
}
_CPBs += _CPB.toList
}
frequencyItemMap.foreach(x => {
if (x._2 < minSupportCount) frequencyItemMap -= x._1
})
val frequencyItems = frequencyItemMap
.toList
.map(x => new FrequencyItem(x._1, x._2))
.sortWith((x,y) => frequencyItemIndex(x.itemName) < frequencyItemIndex(y.itemName))
val fpTree = new FPTree("root", frequencyItems)
println("开是构建FPTree...")
if (frequencyItems.size > 0) {
print("\t打印频繁模式项头:")
frequencyItems.foreach(x => printf("%s:%d ", x.itemName, x.supportCount))
println("")
for (_CPB <- _CPBs) {
val _items = _CPB
.filter(x => frequencyItemMap.isDefinedAt(x.itemName))
.sortWith((x, y) => frequencyItemIndex(x.itemName) < frequencyItemIndex(y.itemName))
print("\t扫描频繁项集合:")
_items.foreach(x => printf("%s:%d ", x.itemName, x.supportCount))
println("")
insertTree(_items, fpTree)
fpTree.resumeCurrentNode
}
} else {
print("\t没有可用条件模式基...")
}
fpTree
}
打印挖掘过程
开启频繁模式挖掘...
建立I5:2的条件模式树:
开是构建FPTree...
打印频繁模式项头:I2:2 I1:2
扫描频繁项集合:I2:1 I1:1
在root下面增加新结点I2:1
把新结点I2:1,加入频繁模式头链表
在I2下面增加新结点I1:1
把新结点I1:1,加入频繁模式头链表
扫描频繁项集合:I2:1 I1:1
增加支持度计数:I2 up to 2
增加支持度计数:I1 up to 2
挖掘I5:2的频繁模式:{I2,I5:2} {I2,I1,I5:2} {I1,I5:2}
建立I4:2的条件模式树:
开是构建FPTree...
打印频繁模式项头:I2:2
扫描频繁项集合:I2:1
在root下面增加新结点I2:1
把新结点I2:1,加入频繁模式头链表
扫描频繁项集合:I2:1
增加支持度计数:I2 up to 2
挖掘I4:2的频繁模式:{I2,I4:2}
建立I3:6的条件模式树:
开是构建FPTree...
打印频繁模式项头:I2:4 I1:4
扫描频繁项集合:I2:2
在root下面增加新结点I2:2
把新结点I2:2,加入频繁模式头链表
扫描频繁项集合:I1:2
在root下面增加新结点I1:2
把新结点I1:2,加入频繁模式头链表
扫描频繁项集合:I2:2 I1:2
增加支持度计数:I2 up to 4
在I2下面增加新结点I1:2
把新结点I1:2,加入频繁模式头链表
挖掘I3:6的频繁模式:{I1,I3:4}
建立I1,I3:4的条件模式树:
开是构建FPTree...
打印频繁模式项头:I2:2
扫描频繁项集合:
扫描频繁项集合:I2:2
在root下面增加新结点I2:2
把新结点I2:2,加入频繁模式头链表
挖掘I1,I3:4的频繁模式:{I2,I1,I3:2}
挖掘I3:6的频繁模式:{I2,I3:4}
建立I1:6的条件模式树:
开是构建FPTree...
打印频繁模式项头:I2:4
扫描频繁项集合:I2:4
在root下面增加新结点I2:4
把新结点I2:4,加入频繁模式头链表
扫描频繁项集合:
挖掘I1:6的频繁模式:{I2,I1:4}
建立I2:7的条件模式树:
开是构建FPTree...
没有可用条件模式基...