树状数组（一）

首先来介绍一下树状数组这个东西：
它是一种很特别的数据结构，在我们暴力求解某个加和（O(n)）然后更改（O(1)），然后再暴力求和（O(n)），然后再更改，然后TLE的过程中，树状数组已经默默地用O（logn）的时间查找+O（logn）的时间更改了整个数据。
嗯没错它非常迅速……
所以为了让我们的程序不TLE，还是需要进行树状数组的学习。
我们先来说一下这个树状数组的实现：
二进制。
用二进制的加法来构造整个树，用二进制的减法来对树进行操作。（感觉自己啥都没说）
在说这个东西之前要说说lowbit。

int lowbit(int x){ 
    return x&(-x);
} 

x的原码是：0balabalabala……
-x就是把x的原码都改成相反的（x^=1）再加一。
所以也可以写成return x=1+(x^1);（似乎是这样吧）
没错就是这样……
关键是lowbit是干啥的？
（最）low（低）bit（位）。
1的最低位。
也就是：100010100 的lowbit是100。
10001011的lowbit是1。
也就是：从右向左数有几个零，然后再在前面补个1。
（刚刚听到李大爷在说线段树又长又慢但是线段树比较应用广泛……于是刚刚学了一点树状数组的我哭晕在厕所）
从厕所里跑出来之后还是要苦哈哈地写博客……
我们知道了lowbit是求1的最低位的东西，那关键是求这个有什么用呢？
我们先欣赏一下树状数组的图吧……

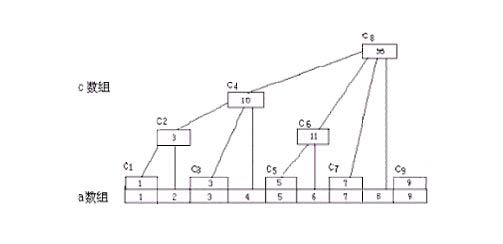
嗯实际上我的图是在网上挖的。
lowbit是可以构造数组（对任意的树状数组都成立），更改数组（对任意的树状数组都成立），求1~任意一个结点的和的（这是在本例中）。
它是通过加减lowbit来实现的。
+lowbit(i)的实质是说：
类似于这个式子：1000100+lowbit(1000100)=1001000。
也就是1的最低位变成0并且它的左边这一位+1。
那关键这样咋办：1001100+lowbit(1001100)=1010000。
实际上就是进位……
那么，-lowbit(i)的实质呢？
100010100-lowbit(100010100)=100010000。
也就是扫掉最后的小尾巴。（最后的那个1变成0）
那在树中的体现是怎样的呢？
显然+lowbit会慢慢地变大，而-lowbit最后会变成0。
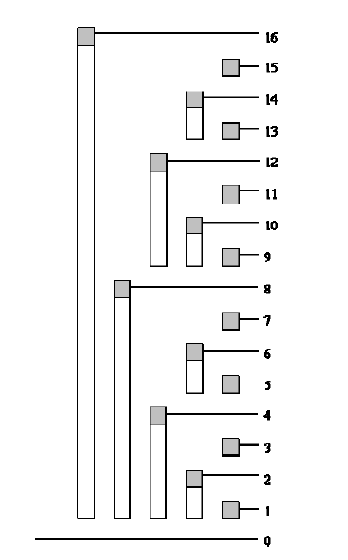
我们不妨拿这张图说话：

1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
16 10000
（网上找的图）
看6(二进制为110)+lowbit（6）==>8（1000）是不是向上走了一个等级？
嗯我们把它当作Level up!（实际上，加上一个lowbit之后会得到该”长条“左侧的那个大长条）
那减lowbit呢？
6-lowbit(6)==>4（100）是的这个等级并没有下降，不过我们可以继续进行操作：
4-lowbit(4)==>0（0）
发现了什么？（看那个长条：4的长条和6的长条加起来刚好是0~6的区间）
嗯没错。-lowbit不是Level down……而是把之前的“长条”都加起来。
那如果这样呢？

for(int i=1;i<=n;i++)
    for(int j=1;j<lowbit(i);j<<=1)
        c[i]+=c[i-j];

我们这样对j进行操作，会使得i-j对应的条是序号为i的这个“条”所能覆盖的所有“条”。（也就是它的“孩子”）。（例如6这个条就会变成5这个条与6本身的和，而5这个条就只能覆盖5，所以它就只能是5了）
实际上一开始我们是先计算小的部分，通过小的部分然后拼凑起大的部分，而我们遍历每个条的lowbit，是对它的“孩子”所得的东西进行统计（也就是合并）。
没错，树状数组是分治思想的一种体现。
我目前发现树状数组支持三种操作：

1.建立”长条“（合并孩子）：for(int i=1;i<=n;i++) for(int j=1;j<lowbit(i);j<<=1);（合并它的孩子）
2.更改（O(logn)）：for(int i=p;i<=n;i+=lowbit(i))｛也就是，把它上面的长条都改了｝
3.区间加和：（从1到q）for(int i=q;i>0;i-=lowbit(i))（也就是计算1~q之间的那个长条的长度）

另外，lowbit的运算遵循一个规则：当一个数不是二的q次幂时，（n-1）表示初始位数。不断地加lowbit加p次后第一次出现的2的整数幂是2的n次幂，不断的减lowbit减q次后第一次出现的2的整数幂是2的（n-1）次幂。
感觉这个规则并没有什么用……
另外附上例题（裸的树状数组模版题）：
HDU 1166 炮兵
代码如下：

/*HDU 1166 炮兵布阵
    完成于11-30 
    基本思路：裸的树状数组题
    第一次打树状数组就对了2333333 
*/
#include <cmath>
#include <algorithm>
#include <ctime>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#include <stack>
#include <iomanip>
#include <iostream>
using namespace std;
int c[50005];
int t,n;
int lowbit(int x){
    return x&(-x);
}
int cg,where;
void sub(){
    scanf("%d%d",&where,&cg);
    for(int i=where;i<=n;i+=lowbit(i))c[i]-=cg;
    return;
}
void add(){
    scanf("%d%d",&where,&cg);
    for(int i=where;i<=n;i+=lowbit(i))c[i]+=cg;
    return;
}
void query(){
    int lc,rc;
    int ansl=0,ansr=0;
    scanf("%d%d",&lc,&rc);
    for(int i=lc-1;i>0;i-=lowbit(i))ansl+=c[i];
    for(int i=rc;i>0;i-=lowbit(i))ansr+=c[i];
    printf("%d\n",ansr-ansl);
    return;
}
int main (){
    scanf("%d",&t);
    int num=0;  
    while(num<t){
        num++;
        memset(c,0,sizeof(c));
        scanf("%d",&n);
        for(int i=1;i<=n;i++)scanf("%d",&c[i]);
        for(int i=1;i<=n;i++)
            for(int j=1;j<lowbit(i);j<<=1)
                c[i]+=c[i-j];
        //     for(int i=1;i<=12;i++)printf("%d ",c[i]);    
        printf("Case %d:\n",num);
        while(1){
            string order;
            cin>>order;
            if(order=="End")break;
            else if(order=="Query")query();             
            else if(order=="Add")add();
            else if(order=="Sub")sub();  
        }
    }
    return 0;
}

总的来说应该就是这样……我现在还只会一维树状数组，需要继续努力学习……