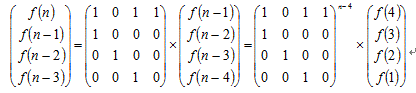集训队专题（2）1004 Queuing

Queuing

Time Limit : 10000/5000ms (Java/Other)   Memory Limit : 32768/32768K (Java/Other)

Total Submission(s) : 29   Accepted Submission(s) : 18

Problem Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 

  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 ^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

 

Input

Input a length L (0 <= L <= 10 [sup]6[/sup]) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

   
   
   
   

    
    
    
    3 8
4 7
4 8
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    6
2
1

   
   
   
   

 

Author

WhereIsHeroFrom

 

Source

HDU 1st “Vegetable-Birds Cup” Programming Open Contest

 

此题首先是一个递推题，第一步：推出其递推公式。这里小编给出一个递推公式的推导过程：

1.当最后一位是m的时候，倒数第二位是什么都可以，故f(n)第一部分为f(n-1)；

2.当最后一位是f的时候，并不能直接判断，所以还要讨论倒数第二位：

(1)当倒数第二位是f的时候，倒数第三位只能是m，此时最后三位为mff，倒数第四位只能是m，故f(n)第二部分为f(n-4)；

(2)当倒数第二位是m的时候，倒数第三位只能是m，此时最后三位为mmf，倒数第四位是什么都可以，故f(n)第三部分为f(n-3)；

综上所述，f(n)=f(n-1)+f(n-3)+f(n-4)。

递推公式已得到，剩下来的就是用矩阵幂去优化了。不难想到，我们可以这样构造矩阵：

矩阵构造好后就可以直接进行快速幂运算啦（小编~）。

#include <cstdio>
#include <cstring>
struct Matrix
{
	int a[6][6];
	int r,c;
};
Matrix ori,res;
int F[5],Ans[5];
void init()
{
	ori.r = ori.c = 4;
	memset(ori.a,0,sizeof(ori.a));
	ori.a[0][0] = ori.a[0][2] = ori.a[0][3] = 1;
	ori.a[1][0] = ori.a[2][1] = ori.a[3][2] = 1;
	res.r = res.c = 4;
	memset(res.a,0, sizeof(res.a));
	res.a[0][0] = res.a[1][1] = res.a[2][2] = res.a[3][3] = 1;
	F[0] = 6,F[1] = 4,F[2] = 2,F[3] = 1;
}
Matrix multi(Matrix x,Matrix y,int m)
{
	Matrix z;
	memset(z.a,0,sizeof(z.a));
	z.r = x.r;
	z.c = y.c;
	for(int i=0; i<x.r; i++)
	{
		for(int k=0; k<x.c; k++)
		{
			if(x.a[i][k] == 0) continue;
			for(int j=0; j<y.c; j++)
				z.a[i][j] = (z.a[i][j] + (x.a[i][k] * y.a[k][j]) % m) % m;
		}
	}
	return z;
}
void fast_mod(int n,int m)
{
	while(n)
	{
		if(n&1)
			res = multi(ori,res,m);
		ori = multi(ori,ori,m);
		n >>= 1;
	}
}
void solve(int n,int m)
{
	fast_mod(n,m);
	memset(Ans,0,sizeof(Ans));
	for(int i=0; i<res.r; i++)
	{
		for(int k=0; k<res.c; k++)
			Ans[i] = (Ans[i] + res.a[i][k] * F[k]) % m;
	}
	printf("%d\n",Ans[0]);
}
int main()
{
	int L,M;
	while(scanf("%d%d",&L,&M)!=EOF)
	{
		Ans[0] = 0,Ans[1] = 2,Ans[2] = 4,Ans[3] = 6;
		if(L <= 3)
		{
			printf("%d\n",Ans[L] % M);
			continue;
		}
		init();
		solve(L-3,M);
	}
	return 0;
}