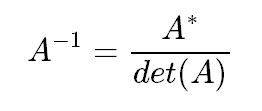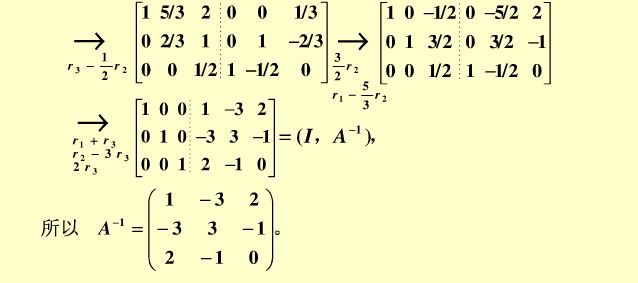3D数学之矩阵的各种求逆
经过三天的准备终于把矩阵的各种求逆方法以及代码完成了。心里有点小激动,come on,来吧,点燃你的心中的那团火,跟着游戏音乐的律动一起跟我走入神秘的3D世界。![]()
下面介绍三种方法:
1.用伴随矩阵求逆
2.用高斯-约当消元法求逆
3.用LU分解求逆(听别人说效率最高)
在介绍方法之前,先阐述几个概念
第一种方法:伴随矩阵
为了求A的逆,我们需要求A*和det(A)
为了求A*,我们需要求C
所以我们需要一个求代数余子式的函数,从而实现一个求代数余子式矩阵的函数
由于求代数余子式中需要求余子阵以及其行列式的值。所以我们需要一个函数实现求余子阵,一个求矩阵的行列式的函数。
为了求det(A),我们也需要一个求矩阵行列式的函数。而行列式的求法又牵涉到代数余子式的求法,所以求行列式的函数与求代数余子式的函数相互嵌套调用,最终出口在求行列式的函数里,即当矩阵只有一个元素的时候。
下面提供实现代码:
matrix的定义如下:
#ifndef MATRIX_H
#define MATRIX_H
#include <iostream>
namespace Seamanj
{
class Matrix
{
protected:
int Nrows,Ncols;
double *data;
public:
Matrix(int rows = 0,int cols = 0,const double *M = NULL);
Matrix(Matrix& m)//深度复制
{
Nrows=m.Nrows;
Ncols=m.Ncols;
data=new double[Nrows*Ncols];
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
(*this)(i,j)=m(i,j);
}
~Matrix();
void setNrows(int i){Nrows=i;}
void setNcols(int i){Ncols=i;}
int getNrows(){return Nrows;}
int getNcols(){return Ncols;}
double& operator()(int i,int j);
double getDetermination();
Matrix getSubmatrixByDeleting_i_row_j_col(int i,int j);
double getCofactor_i_j(int i,int j);
Matrix getCofactorMatrix();
Matrix getTranspose();
Matrix getInverseByAdjugate();
Matrix getInverseByGauss_Jordan_Elimination();
Matrix getInverseByLU_Decompose();
friend Matrix LU_Decompose(Matrix& m, int *index,double* detSign=NULL);
friend void LU_back_substitution(Matrix& m, int *index, double col[],double result[]);
Matrix operator*(double d);
Matrix operator=(Matrix& m);//深度赋值
friend Matrix operator*(double d,Matrix& m);
friend std::ostream& operator<<(std::ostream &os ,Matrix& m);
};
Matrix operator*(double d,Matrix& m);
}
#endif
求余子阵函数的实现
Matrix Matrix::getSubmatrixByDeleting_i_row_j_col(int i,int j)
{
if( i < 0 || j < 0 || i >= Nrows || j >= Ncols )
{
cerr << "getSubmatrixByDeleting_i_row_j_col error!"<<endl;
exit(-1);
}
Matrix sm(getNrows()-1,getNcols()-1);
for(int ii=0;ii<Nrows-1;ii++)
for(int jj=0;jj<Ncols-1;jj++)
{
if(ii < i && jj < j)
sm(ii,jj)=(*this)(ii,jj);
else if(ii < i && jj >= j)
sm(ii,jj)=(*this)(ii,jj+1);
else if(ii >= i && jj < j)
sm(ii,jj)=(*this)(ii+1,jj);
else if(ii >= i && jj >= j)
sm(ii,jj)=(*this)(ii+1,jj+1);
}
return sm;
}
求代数余子式函数的实现
double Matrix::getCofactor_i_j(int i,int j)
{
if( i < 0 || j < 0 || i >= Nrows || j >= Ncols || Nrows != Ncols)
{
cerr << "getCofactor_i_j error"<<endl;
exit(-1);
}
//double d=pow(-1.0,i+j) * getSubmatrixByDeleting_i_row_j_col(i,j).getDetermination();
//这样写是错误的,原因: getSubmatrixByDeleting_i_row_j_col(i,j)返回的是局部的,调用完后会析构
Matrix m=getSubmatrixByDeleting_i_row_j_col(i,j);
double d=pow(-1.0,i+j) * m.getDetermination();
return d;
}
求代数余子式矩阵的实现代码
Matrix Matrix::getCofactorMatrix()
{
Matrix cm(Nrows,Ncols);
for(int i=0;i<cm.getNrows();i++)
for(int j=0;j<cm.getNcols();j++)
cm(i,j)=getCofactor_i_j(i,j);
return cm;
}
求矩阵行列式函数的实现代码
double Matrix::getDetermination()
{
if( Nrows < 1 || Ncols < 1|| Nrows != Ncols)
{
cerr << "getDetermination error"<<endl;
exit(-1);
}
if(Nrows == 1)
return (*this)(0,0);
double sum=0.0;
for(int i=0;i<Ncols;i++)
{
sum+=(*this)(i,0)*getCofactor_i_j(i,0);
}
return sum;
}
最终还需要一个求转置函数,将代数余子式矩阵转置为伴随矩阵
Matrix Matrix::getTranspose()
{
if( Nrows < 1 || Ncols < 1)
{
cerr << "getTranspose error"<<endl;
exit(-1);
}
Matrix tm(Ncols,Nrows);
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
tm(j,i)=(*this)(i,j);
return tm;
}
Matrix Matrix::getInverseByAdjugate()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getInverseByAdjugate error"<<endl;
exit(-1);
}
Matrix m=getCofactorMatrix();
m=m.getTranspose();
double d=getDetermination();
if(d < 1e-6 && d>-1e-6)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
return m *(1/getDetermination());
}
第二种方法:高斯-约当消元法
来个小插曲,为什么叫高斯-约当消元法(Gauss_Jordan_Elimination)呢?
那是因为高斯在消元的时候只想到了往下消元,没有往上消,而约当却想到了往上消,所以叫Gauss_Jordan_Elimination。

对应的代码如下:
Matrix Matrix::getInverseByGauss_Jordan_Elimination()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getgetInverseByGauss_Jordan_Elimination error"<<endl;
exit(-1);
}
Matrix m(Nrows,2*Ncols);
for(int i=0;i<m.Nrows;i++)//求增广矩阵
for(int j=0;j<m.Ncols;j++)
{
if(j<Ncols)
m(i,j)=(*this)(i,j);
else if(j == i+Ncols)
m(i,j)=1;
else
m(i,j)=0;
}
for(int j=0;j<Ncols;j++)//对每列进行消元
{
double max=1e-6;
int maxrow=-1;
for(int i=j;i<Nrows;i++)//找出每列的最大绝对值的元素作为主元
{
if(abs(m(i,j))>max)
{
max=abs(m(i,j));
maxrow=i;
}
}
if(maxrow == -1)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
if(maxrow != j)//换行
{
for(int k=j;k<m.Ncols;k++)
{
double temp;
temp=m(j,k);
m(j,k)=m(maxrow,k);
m(maxrow,k)=temp;
}
}
for(int k=m.Ncols-1;k>=j;k--)//与主元同行的元素(从主元到行末,因为主元前面是0元素,所以没有必要除了)除以主元,注意是从后往前,这样可以保持主元除自己之前保持不变
{
m(j,k)/=m(j,j);
}
for(int k=m.Ncols-1;k>=j;k--)//对每行从后往前进行消元
{
for(int l=0;l<m.Nrows;l++)
{
if(l!=j)
{
m(l,k)-=m(l,j)*m(j,k);
}
}
}
}
Matrix result(Nrows,Ncols);
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
result(i,j)=m(i,j+Ncols);
return result;
}
第三种 利用LU分解求逆
LU分解函数的实现
Matrix LU_Decompose(Matrix& m, int *index,double* detSign)
{
double *rowNormalizer=new double[m.Nrows];
Matrix result(m);
double exchangeParity = 1.0;
//calulate a normalizer for each row
for(int i=0;i<result.Nrows;i++)
{
double maxvalue=0.0;
for(int j=0;j<result.Ncols;j++)
{
if(abs(result(i,j))>maxvalue)
maxvalue=abs(result(i,j));
}
if(maxvalue < 1e-6 && maxvalue > -1e-6)
{
cerr<<"This matrix isn't invertible"<<endl;
delete []rowNormalizer;
exit(-1);
}
rowNormalizer[i]=1.0/maxvalue;
index[i]=i;
}
//Perform decomposition
for(int j=0;j<result.Ncols;j++)
{
for(int i=0;i<j;i++)
{
double sum=result(i,j);
for(int k=0;k<i;k++)
sum-=result(i,k)*result(k,j);
result(i,j)=sum;
}
//Find pivot element
int pivotRow=-1;
double maxvalue=0.0;
for(int i=j;i<result.Nrows;i++)
{
double sum=result(i,j);
for(int k=0;k<j;k++)
sum-=result(i,k)*result(k,j);
result(i,j)=sum;//这里sum已经存入m
sum=abs(sum)*rowNormalizer[i];
if(sum>maxvalue)
{
maxvalue=sum;
pivotRow=i;
}
}
if(pivotRow == -1)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
if(pivotRow!=j)//Exchange rows
{
for(int k=0 ; k<m.Ncols;k++)
{
double temp=result(j,k);
result(j,k)=result(pivotRow,k);
result(pivotRow,k)=temp;
}
int temp=index[j];
index[j]=index[pivotRow];
index[pivotRow]=temp;
rowNormalizer[pivotRow]= rowNormalizer[j];//为什么不交换?因为前面的已经用不到,所以不用交换
exchangeParity = -exchangeParity;
}
//Divide by pivot element
if(j != result.Nrows-1)
{
double denom = 1.0/result(j,j);
for(int i=j+1;i<result.Nrows;i++)
result(i,j)*=denom;
}
}
if(detSign)
*detSign=exchangeParity;
delete []rowNormalizer;
return result;
}
LU回带函数的实现
void LU_back_substitution(Matrix& m, int *index, double col[],double result_col[])
{
for(int i=0;i<m.Nrows;i++)
result_col[i]=col[index[i]];
//Perform forward substitution for Ly=col;
for(int i=0;i<m.Nrows;i++)
{
double sum=result_col[i];
for(int j=0;j<i;j++)
sum-=m(i,j)*result_col[j];
result_col[i]=sum;
}
//Perform backward substitution for Ux=y
for(int i=m.Nrows-1;i>=0;i--)
{
double sum=result_col[i];
for(int j=i+1;j<m.Ncols;j++)
sum-=m(i,j)*result_col[j];
result_col[i]=sum/m(i,i);
}
}
最终通过LU分解求逆的函数如下:
Matrix Matrix::getInverseByLU_Decompose()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getInverseByLU_Decompose error"<<endl;
exit(-1);
}
int* index=new int[Nrows];
double* col=new double[Nrows];
double* result_col=new double[Nrows];
Matrix m= LU_Decompose(*this,index);
Matrix result(Nrows,Ncols);
for(int j=0;j<Ncols;j++)//设置为单位矩阵的每一列
{
for(int i=0;i<Nrows;i++)
if(j==i)
col[i]=1.0;
else
col[i]=0.0;
LU_back_substitution(m,index,col,result_col);
for(int i=0;i<Nrows;i++)
result(i,j)=result_col[i];
}
delete []index;
delete []col;
delete []result_col;
return result;
}
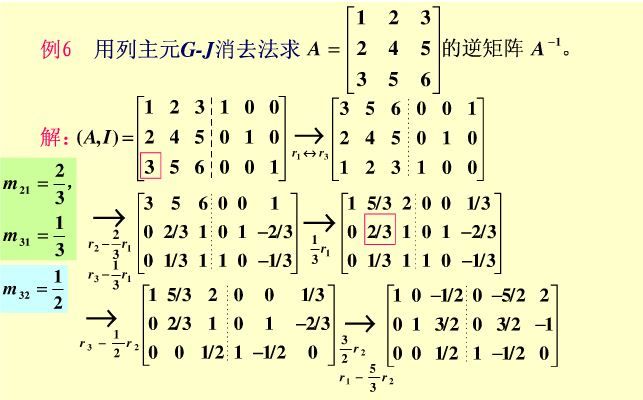
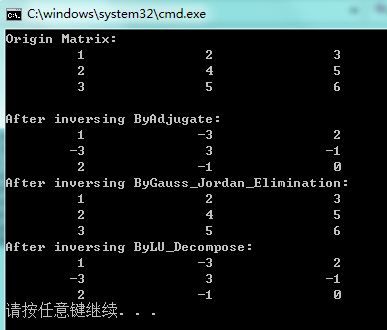
下列通过这三种方法进行验证上面那个高斯消元法介绍的矩阵的求逆
void main()
{
double m_try[9] = {1,2,3,2,4,5,3,5,6};
Seamanj::Matrix myMatrix(3,3,m_try);
cout << "Origin Matrix:" << endl << myMatrix << endl ;
myMatrix=myMatrix.getInverseByAdjugate();
cout << "After inversing ByAdjugate:"<<endl<<myMatrix;
myMatrix=myMatrix.getInverseByGauss_Jordan_Elimination();
cout << "After inversing ByGauss_Jordan_Elimination:"<<endl<<myMatrix;
myMatrix=myMatrix.getInverseByLU_Decompose();
cout<< "After inversing ByLU_Decompose:"<<endl<<myMatrix;
}
结果如下:
最后给出该程序的头文件和源文件
Matrix.h头文件内容:
#ifndef MATRIX_H
#define MATRIX_H
#include <iostream>
namespace Seamanj
{
class Matrix
{
protected:
int Nrows,Ncols;
double *data;
public:
Matrix(int rows = 0,int cols = 0,const double *M = NULL);
Matrix(Matrix& m)//深度复制
{
Nrows=m.Nrows;
Ncols=m.Ncols;
data=new double[Nrows*Ncols];
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
(*this)(i,j)=m(i,j);
}
~Matrix();
void setNrows(int i){Nrows=i;}
void setNcols(int i){Ncols=i;}
int getNrows(){return Nrows;}
int getNcols(){return Ncols;}
double& operator()(int i,int j);
double getDetermination();
Matrix getSubmatrixByDeleting_i_row_j_col(int i,int j);
double getCofactor_i_j(int i,int j);
Matrix getCofactorMatrix();
Matrix getTranspose();
Matrix getInverseByAdjugate();
Matrix getInverseByGauss_Jordan_Elimination();
Matrix getInverseByLU_Decompose();
friend Matrix LU_Decompose(Matrix& m, int *index,double* detSign=NULL);
friend void LU_back_substitution(Matrix& m, int *index, double col[],double result[]);
Matrix operator*(double d);
Matrix operator=(Matrix& m);//深度赋值
friend Matrix operator*(double d,Matrix& m);
friend std::ostream& operator<<(std::ostream &os ,Matrix& m);
};
Matrix operator*(double d,Matrix& m);
}
#endif
Matrix.cpp源文件内容:
#include "Matrix.h"
#include <iomanip>
#include <cmath>
using namespace std;
namespace Seamanj
{
Matrix::Matrix(int rows,int cols,const double *M)
{
if(rows < 0 || cols < 0 || ((rows == 0 || cols == 0) && cols != rows))//注意rows和cols可以同时为0
{
cerr << "Matrix size impossible (negative or zero rows or cols)" << endl;
exit(1);
}
Nrows=rows;
Ncols=cols;
data=new double[Nrows*Ncols];
if(!data)
{
cerr << "not enough memory to allocate " << rows << " x " << cols << " Matrix" << endl;
exit(1);
}
if(M)
{
for(int i=0,k=0;i<rows;i++)
for(int j=0;j<cols;j++)
data[i*rows+j]=M[k++];
}
}
Matrix::~Matrix()
{
delete []data;
}
double& Matrix::operator()(int i,int j)
{
if(i < 0 || i >= Nrows || j < 0 || j >= Ncols)
{
cerr << " Invalid entry for Matrix " << endl;
exit(0);
}
return data[i*Ncols+j];
}
Matrix Matrix::getInverseByGauss_Jordan_Elimination()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getgetInverseByGauss_Jordan_Elimination error"<<endl;
exit(-1);
}
Matrix m(Nrows,2*Ncols);
for(int i=0;i<m.Nrows;i++)//求增广矩阵
for(int j=0;j<m.Ncols;j++)
{
if(j<Ncols)
m(i,j)=(*this)(i,j);
else if(j == i+Ncols)
m(i,j)=1;
else
m(i,j)=0;
}
for(int j=0;j<Ncols;j++)//对每列进行消元
{
double max=1e-6;
int maxrow=-1;
for(int i=j;i<Nrows;i++)//找出每列的最大绝对值的元素作为主元
{
if(abs(m(i,j))>max)
{
max=abs(m(i,j));
maxrow=i;
}
}
if(maxrow == -1)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
if(maxrow != j)//换行
{
for(int k=j;k<m.Ncols;k++)
{
double temp;
temp=m(j,k);
m(j,k)=m(maxrow,k);
m(maxrow,k)=temp;
}
}
for(int k=m.Ncols-1;k>=j;k--)//与主元同行的元素(从主元到行末,因为主元前面是0元素,所以没有必要除了)除以主元,注意是从后往前,这样可以保持主元除自己之前保持不变
{
m(j,k)/=m(j,j);
}
for(int k=m.Ncols-1;k>=j;k--)//对每行从后往前进行消元
{
for(int l=0;l<m.Nrows;l++)
{
if(l!=j)
{
m(l,k)-=m(l,j)*m(j,k);
}
}
}
}
Matrix result(Nrows,Ncols);
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
result(i,j)=m(i,j+Ncols);
return result;
}
Matrix Matrix::getInverseByAdjugate()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getInverseByAdjugate error"<<endl;
exit(-1);
}
Matrix m=getCofactorMatrix();
m=m.getTranspose();
double d=getDetermination();
if(d < 1e-6 && d>-1e-6)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
return m *(1/getDetermination());
}
Matrix Matrix::getCofactorMatrix()
{
Matrix cm(Nrows,Ncols);
for(int i=0;i<cm.getNrows();i++)
for(int j=0;j<cm.getNcols();j++)
cm(i,j)=getCofactor_i_j(i,j);
return cm;
}
double Matrix::getCofactor_i_j(int i,int j)
{
if( i < 0 || j < 0 || i >= Nrows || j >= Ncols || Nrows != Ncols)
{
cerr << "getCofactor_i_j error"<<endl;
exit(-1);
}
//double d=pow(-1.0,i+j) * getSubmatrixByDeleting_i_row_j_col(i,j).getDetermination();
//这样写是错误的,原因: getSubmatrixByDeleting_i_row_j_col(i,j)返回的是局部的,调用完后会析构
Matrix m=getSubmatrixByDeleting_i_row_j_col(i,j);
double d=pow(-1.0,i+j) * m.getDetermination();
return d;
}
Matrix Matrix::getSubmatrixByDeleting_i_row_j_col(int i,int j)
{
if( i < 0 || j < 0 || i >= Nrows || j >= Ncols )
{
cerr << "getSubmatrixByDeleting_i_row_j_col error!"<<endl;
exit(-1);
}
Matrix sm(getNrows()-1,getNcols()-1);
for(int ii=0;ii<Nrows-1;ii++)
for(int jj=0;jj<Ncols-1;jj++)
{
if(ii < i && jj < j)
sm(ii,jj)=(*this)(ii,jj);
else if(ii < i && jj >= j)
sm(ii,jj)=(*this)(ii,jj+1);
else if(ii >= i && jj < j)
sm(ii,jj)=(*this)(ii+1,jj);
else if(ii >= i && jj >= j)
sm(ii,jj)=(*this)(ii+1,jj+1);
}
return sm;
}
double Matrix::getDetermination()
{
if( Nrows < 1 || Ncols < 1|| Nrows != Ncols)
{
cerr << "getDetermination error"<<endl;
exit(-1);
}
if(Nrows == 1)
return (*this)(0,0);
double sum=0.0;
for(int i=0;i<Ncols;i++)
{
sum+=(*this)(i,0)*getCofactor_i_j(i,0);
}
return sum;
}
Matrix Matrix::getTranspose()
{
if( Nrows < 1 || Ncols < 1)
{
cerr << "getTranspose error"<<endl;
exit(-1);
}
Matrix tm(Ncols,Nrows);
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
tm(j,i)=(*this)(i,j);
return tm;
}
Matrix LU_Decompose(Matrix& m, int *index,double* detSign)
{
double *rowNormalizer=new double[m.Nrows];
Matrix result(m);
double exchangeParity = 1.0;
//calulate a normalizer for each row
for(int i=0;i<result.Nrows;i++)
{
double maxvalue=0.0;
for(int j=0;j<result.Ncols;j++)
{
if(abs(result(i,j))>maxvalue)
maxvalue=abs(result(i,j));
}
if(maxvalue < 1e-6 && maxvalue > -1e-6)
{
cerr<<"This matrix isn't invertible"<<endl;
delete []rowNormalizer;
exit(-1);
}
rowNormalizer[i]=1.0/maxvalue;
index[i]=i;
}
//Perform decomposition
for(int j=0;j<result.Ncols;j++)
{
for(int i=0;i<j;i++)
{
double sum=result(i,j);
for(int k=0;k<i;k++)
sum-=result(i,k)*result(k,j);
result(i,j)=sum;
}
//Find pivot element
int pivotRow=-1;
double maxvalue=0.0;
for(int i=j;i<result.Nrows;i++)
{
double sum=result(i,j);
for(int k=0;k<j;k++)
sum-=result(i,k)*result(k,j);
result(i,j)=sum;//这里sum已经存入m
sum=abs(sum)*rowNormalizer[i];
if(sum>maxvalue)
{
maxvalue=sum;
pivotRow=i;
}
}
if(pivotRow == -1)
{
cerr<<"This matrix isn't invertible"<<endl;
exit(-1);
}
if(pivotRow!=j)//Exchange rows
{
for(int k=0 ; k<m.Ncols;k++)
{
double temp=result(j,k);
result(j,k)=result(pivotRow,k);
result(pivotRow,k)=temp;
}
int temp=index[j];
index[j]=index[pivotRow];
index[pivotRow]=temp;
rowNormalizer[pivotRow]= rowNormalizer[j];//为什么不交换?因为前面的已经用不到,所以不用交换
exchangeParity = -exchangeParity;
}
//Divide by pivot element
if(j != result.Nrows-1)
{
double denom = 1.0/result(j,j);
for(int i=j+1;i<result.Nrows;i++)
result(i,j)*=denom;
}
}
if(detSign)
*detSign=exchangeParity;
delete []rowNormalizer;
return result;
}
void LU_back_substitution(Matrix& m, int *index, double col[],double result_col[])
{
for(int i=0;i<m.Nrows;i++)
result_col[i]=col[index[i]];
//Perform forward substitution for Ly=col;
for(int i=0;i<m.Nrows;i++)
{
double sum=result_col[i];
for(int j=0;j<i;j++)
sum-=m(i,j)*result_col[j];
result_col[i]=sum;
}
//Perform backward substitution for Ux=y
for(int i=m.Nrows-1;i>=0;i--)
{
double sum=result_col[i];
for(int j=i+1;j<m.Ncols;j++)
sum-=m(i,j)*result_col[j];
result_col[i]=sum/m(i,i);
}
}
Matrix Matrix::getInverseByLU_Decompose()
{
if(Nrows != Ncols || Nrows < 1)
{
cerr << "getInverseByLU_Decompose error"<<endl;
exit(-1);
}
int* index=new int[Nrows];
double* col=new double[Nrows];
double* result_col=new double[Nrows];
Matrix m= LU_Decompose(*this,index);
Matrix result(Nrows,Ncols);
for(int j=0;j<Ncols;j++)//设置为单位矩阵的每一列
{
for(int i=0;i<Nrows;i++)
if(j==i)
col[i]=1.0;
else
col[i]=0.0;
LU_back_substitution(m,index,col,result_col);
for(int i=0;i<Nrows;i++)
result(i,j)=result_col[i];
}
delete []index;
delete []col;
delete []result_col;
return result;
}
Matrix Matrix::operator=(Matrix& m)
{
Nrows=m.Nrows;
Ncols=m.Ncols;
data=new double[Nrows*Ncols];
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
(*this)(i,j)=m(i,j);
return *this;
}
Matrix Matrix::operator*(double d)
{
Matrix m(Nrows,Ncols);
for(int i=0;i<Nrows;i++)
for(int j=0;j<Ncols;j++)
m(i,j)=(*this)(i,j)*d;
return m;
}
Matrix operator*(double d,Matrix& m)//定义友元的时候不能加friend,只有在类里声明友元函数时才能加friend
{
Matrix result(m.getNrows(),m.getNcols());
for(int i=0;i<m.getNrows();i++)
for(int j=0;j<m.getNcols();j++)
result(i,j)=m(i,j)*d;
return result;
}
ostream& operator<<(ostream &os,Matrix& m)
{
for(int i=0;i<m.Nrows;i++)
{
for(int j=0;j<m.Ncols;j++)
os<<setw(10)<<((m(i,j)<1e-6 && m(i,j)>-1e-6)?0.0:m(i,j))<<'\t';
os<<endl;
}
return os;
}
}
void main()
{
double m_try[9] = {1,2,3,2,4,5,3,5,6};
Seamanj::Matrix myMatrix(3,3,m_try);
cout << "Origin Matrix:" << endl << myMatrix << endl ;
myMatrix=myMatrix.getInverseByAdjugate();
cout << "After inversing ByAdjugate:"<<endl<<myMatrix;
myMatrix=myMatrix.getInverseByGauss_Jordan_Elimination();
cout << "After inversing ByGauss_Jordan_Elimination:"<<endl<<myMatrix;
myMatrix=myMatrix.getInverseByLU_Decompose();
cout<< "After inversing ByLU_Decompose:"<<endl<<myMatrix;
}
可执行程序以及相关源代码请点击这里下载