八皇后问题
本文地址:http://blog.csdn.net/spch2008/article/details/9152713
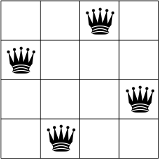
为求简单起见,先看四皇后问题。
所谓皇后问题,即任意两个皇后不能处于同一列,也不能同时处于同一行,而且还不能处于同一对角线上。
我们以列为单位进行放置,即同一列仅放置一个皇后,
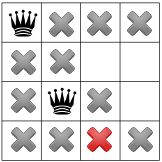
1. 假设将皇后放于第一行第一列,则同一行,同一列,对角线上,均不能放置皇后
首先检测对角线,将污染位置用红X表示。
接下来将同一行的污染位置标记为红X
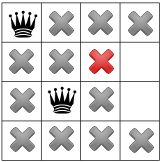
2. 放置第二个皇后
先检测主对角线,将污染位置做标记。
接下来检测辅对角线,标记污染位置。
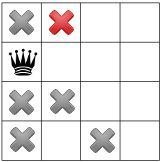
3. 第三个皇后无法放置,所以必须回溯,重新放置第二个皇后,但同样无法的解。
所以回退到第一步,重新放置第一个皇后的位置。
先检测主对角线
然后是辅对角线
然后是同一行,并放置第二个皇后
主,辅对角线
同一行,并放置皇后
主,辅对角线,同一行,并放皇后
上图即得到一个解。
用一个四原数组记录所得解,数组中每个元素对应棋盘的一列。
例如,上述解可以表示为[2, 4, 1, 3],即第一个皇后放在
第1列第2行,第二个皇后放在第2列第4行,第三个皇后放在
第3列第1行,第四个皇后放在第4列第3行。
我们用result来命名这个数组,
首先有一个检测函数,检测是否可以放置。原理:检测同一行是否有皇后,并检测主辅对角线上是否有皇后,
主辅对角线可根据斜率正负1来判断。
bool place(int *result, int row)
{
for(int i = 1; i < row; i++)
{
if(result[i] == result[row] || abs(i-row) == abs(result[i] - result[row]) )
return false;
}
return true;
}
参数row为正在处理的列,而result[row]为该皇后放置的行。检测该皇后是否与已放置的皇后处于同一行,同时通过斜率检测对角线是否有皇后。
int queen(int n)
{
//抛弃下标为0的元素,从1开始
int *result = new int[n+1];
int row = 1;
int total = 0;
//result初始化
for(int i = 1; i <=n; i++)
result[i] = 0;
while(row >= 1)
{
//首先放置在第一行
result[row] += 1;
//检测该位置是否可以放置,如果不可,放到下一位置,即下一行
while(result[row] <= n && !place(result, row) )
result[row] += 1;
//找到一个解
if(result[row] <= n && row == n)
{
total++;
}
//放置下一皇后
else if(result[row] <= n && row < n)
{
row++;
}
//放置失败,回退到上一皇后,重新放置
else
{
//由于没有放置成功,所以需要置0
result[row] = 0;
//回退到上一个皇后处
row--;
}
}
return total;
}
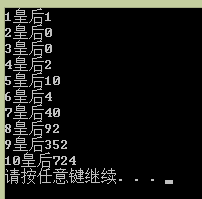
main函数及结果。
int _tmain(int argc, _TCHAR* argv[])
{
for(int i = 1; i <= 10; i++)
cout << i << "皇后" << queen(i) << endl;
system("pause");
return 0;
}
同样,皇后问题也可以通过递归来解决。
bool place(int *result, int row)
{
for(int i = 1; i < row; i++)
{
if(result[i] == result[row] || abs(i-row) == abs(result[i] - result[row]) )
return false;
}
return true;
}
void recursion(int *result, int row, int N, int &total)
{
if(row > N)
total++;
else
{
for(int line = 1; line <= N; line++)
{
result[row] = line;
if( place(result, row) == true)
recursion(result, row+1, N, total);
}
}
}
int queen(int N)
{
int *arr = new int[N+1];
for(int i = 1; i <= N; i++)
arr[i] = 0;
int total = 0;
recursion(arr, 1, N, total);
return total;
}