[置顶] Stereo Matching文献笔记之(十):经典算法Semi-Global Matching(SGM)之碉堡的动态规划~
上一篇博客中提到了SGM的第一部分,基于分层互信息(HMI)的代价计算,本文继续说说自己对SGM代价聚合部分的理解。
(转载请注明:http://blog.csdn.net/wsj998689aa/article/details/50488249, 作者:迷雾forest)
SGM的代价聚合,其实仔细看看,这并不是严格意义上的代价聚合,因为SGM是为了优化一个能量函数,这和一般的全局算法一样,如何利用优化算法求解复杂的能量函数才是重中之重,其能量函数如下所示:
其中,C(p, Dp)代表的就是基于互信息的代价计算项,后面两项指的是当前像素p和其邻域内所有像素q之间的约束,如果q和p的视差只差了1,那么惩罚P1,如果大于1,那么惩罚P2,这么做基本上是机器学习中的常用方法,即所谓的正则化约束。这里需要注意的是,P2要大于P1,这么做真心有用。
1. 假如不考虑像素之间的制约关系,不假设领域内像素应该具有相同的视差值,那么最小化E(D)就是最小化每一个C,这样的视差图效果很差,因为图像总会收到光照,噪声等因素的影响,最小的代价对应的视差往往是“假的”,并且这样做全然不考虑相邻之间的像素关系,例如,一个桌面的视差明显应该相同,但是可能由于倾斜光照的影响,每个像素的最小代价往往会不同,所以看起来就会乱七八糟,东一块西一块。这就是加上约束的目的。
2. 添加两个正则化项一方面是为了保证视差图平滑,另一方面为了保持边缘(保持边缘一直没想明白为什么?)。惩罚的越大,说明越不想看到这种情况发生,具体来说,如果q和p之间的视差有所差异但又不大,那么就要付出代价,你不是想最小化能量函数么?那么二者都要小,如果没有第二项,那么求出来的视差图将会有明显的锯齿现象,如果只有第三项,那么求出来的视差图边缘部分将会得到保持,但由于没有对相差为1的相邻像素进行惩罚,物体内部很可能出现一个“斜面”。
3. 这事情还没完,本文中有对这两项的解释,原文内容如下所示:
这句话的隐含意思是,如果我们让P1<P2,那么会允许出现小的斜面,也会保持边缘,前面一句我理解,惩罚的力度不大,就会导致这种事情还会发生,这也正是作者想看到的,水至清而无鱼嘛,不过,后一句中的P2并不是常数项,是根据相邻像素的差距来决定的,括号里面的“与大小无关”看起来就更加矛盾了,不知道哪位可以给好好解释一下这句话?
有了能量函数,下面要做的就是求解它了,这个时候问题来了,这个E对p是不可导的,这意味着我们常看到的梯度下降,牛顿高斯等等算法在这里都不适用,作者于是采用了动态规划来解决这一问题,动态规划相信大家都知道了,但是其真正的精髓却是深藏不露,我早在大三期间就接触到了动态规划算法,这么多年过去了,虽然时而会用到这个算法,但到现在仍旧不敢说自己彻底懂它。。。。
简单地说,p的代价想要最小,那么前提必须是邻域内的点q的代价最小,q想要代价最小,那么必须保证q的领域点m的代价最小,如此传递下去。
![[置顶] Stereo Matching文献笔记之(十):经典算法Semi-Global Matching(SGM)之碉堡的动态规划~_第1张图片](http://img.e-com-net.com/image/info5/10e454b7a40e432f9c34f8359c5efcca.jpg)
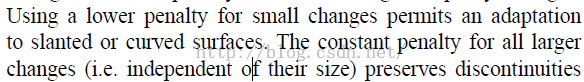
![[置顶] Stereo Matching文献笔记之(十):经典算法Semi-Global Matching(SGM)之碉堡的动态规划~_第2张图片](http://img.e-com-net.com/image/info5/566c19c0b81a45959ec043e5598e6261.jpg)
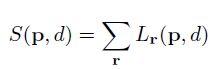
![[置顶] Stereo Matching文献笔记之(十):经典算法Semi-Global Matching(SGM)之碉堡的动态规划~_第3张图片](http://img.e-com-net.com/image/info5/897ce88318bd447580ff200289c313e7.jpg)
