图——从一个顶点到其余各顶点的最短路径——狄克斯特拉算法
/*
*Copyright (c) 2015 , 烟台大学计算机学院
*All right resvered .
*文件名称: Dijkstra算法.cpp
*作 者: 郑兆涵
*图——从一个顶点到其余各顶点的最短路径——狄克斯特拉算法
*/
问题:
从一个顶点到其余各顶点的最短路径——狄克斯特拉算法
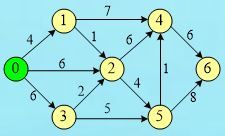
测试用图为:
编程代码:
//头文件:graph.h,包含定义图数据结构的代码、宏定义、要实现算法的函数的声明
#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED
#define MAXV 100 //最大顶点个数
#define INF 32767 //INF表示∞
typedef int InfoType;
//以下定义邻接矩阵类型
typedef struct
{
int no; //顶点编号
InfoType info; //顶点其他信息,在此存放带权图权值
} VertexType; //顶点类型
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
VertexType vexs[MAXV]; //存放顶点信息
} MGraph; //图的邻接矩阵类型
//以下定义邻接表类型
typedef struct ANode //弧的结点结构类型
{
int adjvex; //该弧的终点位置
struct ANode *nextarc; //指向下一条弧的指针
InfoType info; //该弧的相关信息,这里用于存放权值
} ArcNode;
typedef int Vertex;
typedef struct Vnode //邻接表头结点的类型
{
Vertex data; //顶点信息
int count; //存放顶点入度,只在拓扑排序中用
ArcNode *firstarc; //指向第一条弧
} VNode;
typedef VNode AdjList[MAXV]; //AdjList是邻接表类型
typedef struct
{
AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} ALGraph; //图的邻接表类型
//功能:由一个反映图中顶点邻接关系的二维数组,构造出用邻接矩阵存储的图
//参数:Arr - 数组名,由于形式参数为二维数组时必须给出每行的元素个数,在此将参数Arr声明为一维数组名(指向int的指针)
// n - 矩阵的阶数
// g - 要构造出来的邻接矩阵数据结构
void ArrayToMat(int *Arr, int n, MGraph &g); //用普通数组构造图的邻接矩阵
void ArrayToList(int *Arr, int n, ALGraph *&); //用普通数组构造图的邻接表
void MatToList(MGraph g,ALGraph *&G);//将邻接矩阵g转换成邻接表G
void ListToMat(ALGraph *G,MGraph &g);//将邻接表G转换成邻接矩阵g
void DispMat(MGraph g);//输出邻接矩阵g
void DispAdj(ALGraph *G);//输出邻接表G
#endif // GRAPH_H_INCLUDED
//源文件:graph.cpp,包含实现各种算法的函数的定义
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
//功能:由一个反映图中顶点邻接关系的二维数组,构造出用邻接矩阵存储的图
//参数:Arr - 数组名,由于形式参数为二维数组时必须给出每行的元素个数,在此将参数Arr声明为一维数组名(指向int的指针)
// n - 矩阵的阶数
// g - 要构造出来的邻接矩阵数据结构
void ArrayToMat(int *Arr, int n, MGraph &g)
{
int i,j,count=0; //count用于统计边数,即矩阵中非0元素个数
g.n=n;
for (i=0; i<g.n; i++)
for (j=0; j<g.n; j++)
{
g.edges[i][j]=Arr[i*n+j]; //将Arr看作n×n的二维数组,Arr[i*n+j]即是Arr[i][j],计算存储位置的功夫在此应用
if(g.edges[i][j]!=0)
count++;
}
g.e=count;
}
void ArrayToList(int *Arr, int n, ALGraph *&G)
{
int i,j,count=0; //count用于统计边数,即矩阵中非0元素个数
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
G->n=n;
for (i=0; i<n; i++) //给邻接表中所有头节点的指针域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<n; i++) //检查邻接矩阵中每个元素
for (j=n-1; j>=0; j--)
if (Arr[i*n+j]!=0) //存在一条边,将Arr看作n×n的二维数组,Arr[i*n+j]即是Arr[i][j]
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->adjvex=j;
p->info=Arr[i*n+j];
p->nextarc=G->adjlist[i].firstarc; //采用头插法插入*p
G->adjlist[i].firstarc=p;
}
G->e=count;
}
void MatToList(MGraph g, ALGraph *&G)
//将邻接矩阵g转换成邻接表G
{
int i,j;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
for (i=0; i<g.n; i++) //给邻接表中所有头节点的指针域置初值
G->adjlist[i].firstarc=NULL;
for (i=0; i<g.n; i++) //检查邻接矩阵中每个元素
for (j=g.n-1; j>=0; j--)
if (g.edges[i][j]!=0) //存在一条边
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->adjvex=j;
p->info=g.edges[i][j];
p->nextarc=G->adjlist[i].firstarc; //采用头插法插入*p
G->adjlist[i].firstarc=p;
}
G->n=g.n;
G->e=g.e;
}
void ListToMat(ALGraph *G,MGraph &g)
//将邻接表G转换成邻接矩阵g
{
int i,j;
ArcNode *p;
g.n=G->n; //根据一楼同学“举报”改的。g.n未赋值,下面的初始化不起作用
g.e=G->e;
for (i=0; i<g.n; i++) //先初始化邻接矩阵
for (j=0; j<g.n; j++)
g.edges[i][j]=0;
for (i=0; i<G->n; i++) //根据邻接表,为邻接矩阵赋值
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
g.edges[i][p->adjvex]=p->info;
p=p->nextarc;
}
}
}
void DispMat(MGraph g)
//输出邻接矩阵g
{
int i,j;
for (i=0; i<g.n; i++)
{
for (j=0; j<g.n; j++)
if (g.edges[i][j]==INF)
printf("%3s","∞");
else
printf("%3d",g.edges[i][j]);
printf("\n");
}
}
void DispAdj(ALGraph *G)
//输出邻接表G
{
int i;
ArcNode *p;
for (i=0; i<G->n; i++)
{
p=G->adjlist[i].firstarc;
printf("%3d: ",i);
while (p!=NULL)
{
printf("-->%d/%d ",p->adjvex,p->info);
p=p->nextarc;
}
printf("\n");
}
}
//编写main函数,进行相关测试
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
#define MaxSize 100
void Ppath(int path[],int i,int v) //前向递归查找路径上的顶点
{
int k;
k=path[i];
if (k==v) return; //找到了起点则返回
Ppath(path,k,v); //找顶点k的前一个顶点
printf("%d,",k); //输出顶点k
}
void Dispath(int dist[],int path[],int s[],int n,int v)
{
int i;
for (i=0; i<n; i++)
if (s[i]==1)
{
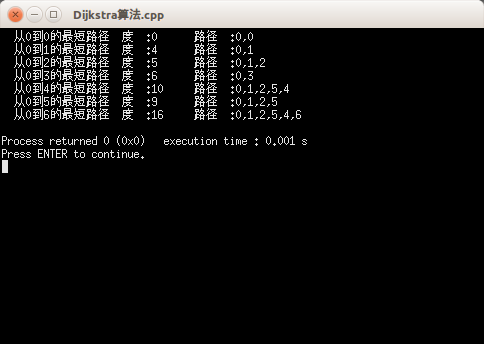
printf(" 从%d到%d的最短路径长度为:%d\t路径为:",v,i,dist[i]);
printf("%d,",v); //输出路径上的起点
Ppath(path,i,v); //输出路径上的中间点
printf("%d\n",i); //输出路径上的终点
}
else printf("从%d到%d不存在路径\n",v,i);
}
void Dijkstra(MGraph g,int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0; i<g.n; i++)
{
dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v;
else
path[i]=-1;
}
s[v]=1;
path[v]=0; //源点编号v放入s中
for (i=0; i<g.n; i++) //循环直到所有顶点的最短路径都求出
{
mindis=INF; //mindis置最小长度初值
for (j=0; j<g.n; j++) //选取不在s中且具有最小距离的顶点u
if (s[j]==0 && dist[j]<mindis)
{
u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入s中
for (j=0; j<g.n; j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF && dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
int main()
{
MGraph g;
int A[7][7]=
{
{0,4,6,6,INF,INF,INF},
{INF,0,1,INF,7,INF,INF},
{INF,INF,0,INF,6,4,INF},
{INF,INF,2,0,INF,5,INF},
{INF,INF,INF,INF,0,INF,6},
{INF,INF,INF,INF,1,0,8},
{INF,INF,INF,INF,INF,INF,0}
};
ArrayToMat(A[0], 7, g);
Dijkstra(g,0);
return 0;
}
输出结果:
我的学习心得:
以上代码取自老师的代码,
根据学习方案的问题,我又从新对下图进行了分析,以及将原先的A[7][7],从新改写为A[6][6]的邻接数组,并进行相关测试:
测试用图为:
int main()
{
MGraph g;
int A[6][6]=
{
{0,50,10,INF,45,INF},
{INF,0,15,INF,5,INF},
{20,INF,0,15,INF,INF},
{INF,20,INF,0,35,INF},
{INF,INF,INF,30,0,INF},
{INF,INF,INF,3,INF,0},
};
ArrayToMat(A[0], 6, g);
Dijkstra(g,0);
return 0;
}
邻接矩阵为:
输出结果:
我的学习心得:
一、最短路径:
对无权图:
(1)若从一顶点到另一顶点存在着一条路径,则称该路径长度为该路径上所有经过的边的数目,它等于该路径上的顶点数减1.
(2)由于从一顶点到另一顶点可能存在着多条路径,每条路径上所经过的边数可能不同,即路径长度不同,我们把路径长度最短(即经过的边数最少)的那条路径叫做最短路径,其路径长度叫做最短路径长度或最短距离。
对带权图:
(1)对于带权图,考虑路径上各边上的权值,则通常把一条路径上所经边的权值之和定义为该路径的路径长度或称带权路径长度。
(2)从源点到终点可能不止一条路径,把带权路径长度最短的那条路径称为最短路径,其路径长度(权值之和)称为最短路径长度或最短距离。
二、从一个顶点到其余各顶点的最短路径问题:
给定一个带权有向图G与源点v,求从v到G中其他顶点的最短路径,并限定各边上的权值大于或等于0.
狄克斯特拉(Dijkstra)算法基本思想:
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组:
第一组为已求出最短路径的顶点集合,用S表示,初值为{v},渐增至V。
第二组为其余未确定最短路径的顶点集合,用U表示。
按最短路径长度递增次序依次把第二组的顶点加入S中,在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
注意:当已加入S中的元素a-----b之间再加入一个c,发现a-----c-----b之间的路径长度小于原a-----b之间的路径长度,则需要保留a-----c-----b这条最短路径。也就是说,每当加入新的一个节点元素的时候,都需要用之前的路径与新产生的路径之间做比较,选择出最短路径进行保留。