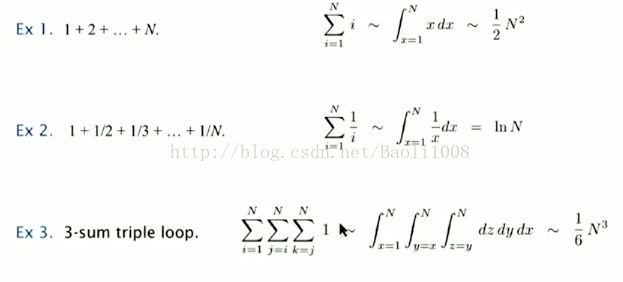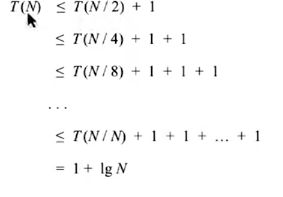Week 1 Analysis of Algorithm(算法分析)

1. Introduction:

本节对算法优化的重要性做了一个概括

两个由算法改进得以优化的技术：

1. Discrete Fourier Transform( 离散傅立叶变换）：使用 FFT（快速傅立叶变换）把时间复杂度由O(N)降为O（log N）

2. N-body Simulation（N体模拟）（天文学）： 使用 Barnes-Hut算法 ，把时间复杂度由O(N)降为O（log N）

还指出了算法优化的流程就是假设和观察相结合直到两者吻合。

2.Observations：

本节介绍了观察的一些方法

首先是观察程序的运行时间和数据量的关系：

建立图像时，一种方法是正常建立，既x轴是数据量，y轴是时间。还有一种log-log Plot，既对x轴和y轴都取对数。

按这个坐标系，许多时候图像会是一条直线，这样可以很方便的对函数做出假设

此时 log(T(n)) = b*log N+ c  (b,c由直线图像得)

推导得 T(n)=2^(b*log N+ c)=2^c*N^b

做出假设

上面这个方程中的b 由算法和数据规模决定，而c由算法，数据规模及硬件环境决定

3.Mathmatical Models:

     1)   Knuth 提出run time=cost*frequency。 其中cost取决于硬件和编译器，frequency取决于算法和输入数据

     2）一些基本操作需要时间：(单位：十亿分之一秒 机型：mac pro）

            int型操作:     add   2.1       multiply   2.4     divide 5.4

           float型操作：     add   4.6     multiply     4.2      divide   13.5

           其他复杂操作：  sin(e)   91.3    arctan(e)   139.7

           可以发现float型操作比int型略高，除法比其他基本运算略高，高级运算明显高于基本操作

           

            学完计算机组成原理后才明白，除法比乘法慢是因为乘法在硬件设计时可以并行计算，除法不行。

      3）估算时间复杂度时忽略低阶项

            一个小知识：

            for(int i=0;i<n;i++){

                    for(int j=i+1;j<n;j++){

                           for(int k=j+1;k<n;k++){。。。。}}}的循环次数是n*(n-1)*(n-2)/3!

       4）计算运算次数的一个好方法是运用积分：

            把级数转换成连续的积分

    

          

            这是一个非常方便的方法

            其实就是求一致收敛的函数性级数的逐步积分法

   

4.Order-of-Growth Classification

     1)复杂度主要只有以下几种：

     1,logN,N,NlogN,N^2,N^3,2^N

      在log log坐标系中他们都是直线：

如图，可见logN的复杂度在n很大时几乎接近O（1）

                  2) 二分搜索：

         公开课中给出的代码为：

int BinarySearch(int a[],int length,int key){
    int l=0,r=length-1;
    while (l<=r) {
        int mid=l+(r-l)/2;
        if(a[mid]==key)return mid;
        else if(a[mid]<key) l=mid-1;
        else if(a[mid]>key) r=mid+1;
    }
    return -1;
}

        始终保证这个不等式成立：a[l]<=key<=a[r]

               

                算法的最差时间复杂度为1+log N

         证明：

         设T(N)为对长度为N的序列二分搜索的时间

5.