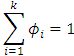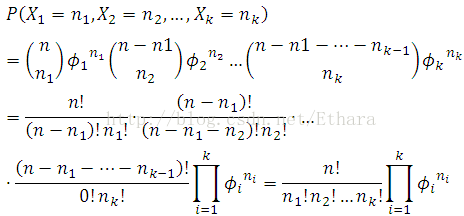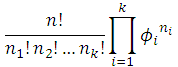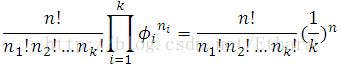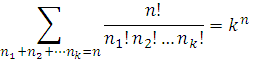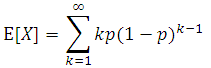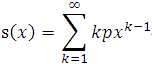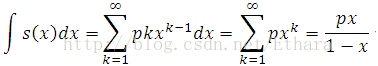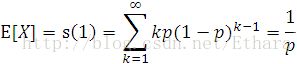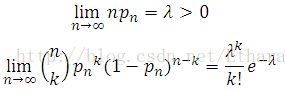猜数字游戏代码:importrandomdefpythonit():a=random.randint(1,100)n=int(input("输入你猜想的数字:"))whilen!=a:ifn>a:print("很遗憾,猜大了")n=int(input("请再次输入你猜想的数字:"))elifna::如果玩家猜的数字n大于随机数字a,则输出"很遗憾,猜大了",并提示玩家再次输入。elifn
基于Google authentic实现的双因子登录认证系统前后台基于SSMP+Vue+Element(解决SecureRandom造成的服务器请求缓慢)
Tate_Brown
gitJAVAIDEADEBUGVUE
用md5两次加盐密码,可以灵活更换算法--直接上代码地址:JAVA后台:https://github.com/TateBrownJava/TwoFALogindemoBackendVue前端:https://github.com/TateBrownJava/TwoFALoginDemofrontend-------------------------------------------------
Open3D 使用RANSAC分割平面
今夕是何年,
单目+双目计算机视觉
目录1,概述2,拟合平面3,实现过程4,主要函数:defsegment_plane(self,distance_threshold,ransac_n,num_iterations):'''5,代码实现6,结果展示1,概述随机抽样一致性算法QRANSAC(Randomsampleconsensus)是一种迭代的方法来从一系列包含有离异值的数据中计算数学模型参数的方法。RANSAC算法本质上由两步组成
groupby 中如何显示 tqdm 的进度条?
domodo2020
在循环时调用tqdm显示进度已经是一个常规操作,常见的方式是foriiintqdm(...):...while循环的情况类似,whileicntintqdm(range(n)):...icnt+=1这里记录没有显式循环时,在groupby中的用法:importpandasaspdimportnumpyasnpfromtqdmimporttqdmdf=pd.DataFrame(np.random.r
Python——俄罗斯方块
星和月
pythonpygame开发语言
俄罗斯方块游戏是一款经典的益智游戏,通常使用编程语言Python来实现。下面是一个简单的俄罗斯方块游戏的示例代码:importpygameimportrandom#定义颜色BLACK=(0,0,0)WHITE=(255,255,255)RED=(255,0,0)GREEN=(0,255,0)BLUE=(0,0,255)CYAN=(0,255,255)MAGENTA=(255,0,255)YELLO
python有趣游戏代码大全
uolo_python
游戏
一.贪吃蛇运行以下代码,将会弹出一个窗口显示贪吃蛇游戏。你可以使用箭头键控制贪吃蛇的移动。吃到食物后蛇的长度会增加,如果蛇触碰到边界或者自己则游戏结束。按下Q键退出游戏,按下C键重新开始游戏。importpygameimportrandom#初始化pygame.init()#设置游戏窗口window_width,window_height=640,480window=pygame.display.
python数组的基本操作
迟遇3
python开发语言
一.创建数组arr:list[int]=[0]*8num1:list[int]=[1,5,9,8,6]二.访问元素1.指定访问(通过索引(下标))defrandom_a(nums:list[int])->int:returnnums[2]print(random_a(arr))2.随机访问(会访问不同的元素)defrandom_access(nums:list[int])->int:"""随机访问
概率图模型(PGM)综述
医学影像处理
概率图模型概率图模型综述
RefLink:http://www.sigvc.org/bbs/thread-728-1-1.htmlGraphicalModel的基本类型基本的GraphicalModel可以大致分为两个类别:贝叶斯网络(BayesianNetwork)和马尔可夫随机场(MarkovRandomField)。它们的主要区别在于采用不同类型的图来表达变量之间的关系:贝叶斯网络采用有向无环图(DirectedAc
qt 创建随机数
入梦游
qt
qt中有两种创建随机数的方法,一种是旧方法,一种是新方法目录旧方法:已过时intqrand()voidqsrand(uintseed)Example新方法QRandomGenerator::global()->bouned(inthighest)QRandomGenerator::global()->generate()更多旧方法:已过时intqrand()生成一个伪随机数,可以使用qsrand(
C++ STL概念之 算法
元凌丶
算法c++开发语言
sortdefault(1)templatevoidsort(RandomAccessIteratorfirst,RandomAccessIteratorlast);custom(2)templatevoidsort(RandomAccessIteratorfirst,RandomAccessIteratorlast,Comparecomp);作用:用于对容器中的元素进行排序。它通常采用快速排序算
开源项目 Kubernetes 源码探索与部署指南
邹滢朦
开源项目Kubernetes源码探索与部署指南kubernetesThisistherepothattracksallpatchestotheOpenShiftdistributionofKubernetesonbranchescorrespondingtoOpenShiftreleases.Seehttps://github.com/openshift/kubernetes/blob/maste
YOLOv8数据增强
热心小张
研究生yolov8
1.找到augment.py(ultralytics/data/augment.py),修改对应内容#TransformsT=[A.Blur(p=0.01),A.MedianBlur(p=0.01),A.ToGray(p=0.01),A.CLAHE(p=0.01),A.RandomBrightnessContrast(p=0.0),A.RandomGamma(p=0.0),A.ImageCompr
计算机视觉中的数据增强方法总结
CV技术指南(公众号)
CV技术总结计算机视觉深度学习卷积神经网络
前言:在计算机视觉方向,数据增强的本质是人为地引入人视觉上的先验知识,可以很好地提升模型的性能,目前基本成为模型的标配。最近几年逐渐出了很多新的数据增强方法,在本文将对数据增强做一个总结。本文介绍了数据增强的作用,数据增强的分类,数据增强的常用方法,一些特殊的方法,如Cutout,RandomErasing,Mixup,Hide-and-Seek,CutMix,GridMask,FenceMask
基于VGG的猫狗识别
卑微小鹿
tensorflowtensorflow
由于猫和狗的数据在这里,所以就做了一下分类的神经网络1、首先进行图像处理:importcsvimportglobimportosimportrandomos.environ['TF_CPP_MIN_LOG_LEVEL']='2'importtensorflowastffromtensorflowimportkerasfromtensorflow.kerasimportlayersimportnum
RAM(随机存取存储器)都有哪些?(超详细)
嵌入式-JY老师
嵌入式工程师c语言硬件架构智能硬件嵌入式硬件
目录RAM的特点RAM的类型1.SRAM(静态随机存取存储器)2.DRAM(动态随机存取存储器)3.SDRAM(同步动态随机存取存储器)4.DDRSDRAM(双倍数据速率同步动态随机存取存储器)5.RDRAM(Rambus动态随机存取存储器)6.VRAM(视频随机存取存储器)7.MRAM(磁阻随机存取存储器)8.FeRAM(铁电随机存取存储器)RAM(RandomAccessMemory,随机存取
使用爬虫写一个简易的翻译器+图像界面+python
w²大大
python学习pythontkinterjson
翻译器+图像界面+python1.效果图如下:2.代码实现1.效果图如下:2.代码实现importtkinterimportrandomimportrequestsimportrequestimporturllibfromurllibimportrequest,parseimporttime,json,random,hashlibwin=tkinter.Tk()defpachong():try:u
Python小游戏——雷霆战机
星和月
pygamepython开发语言
importpygameimportrandom#初始化pygame.init()#定义游戏窗口大小window_width=800window_height=600#创建游戏窗口window=pygame.display.set_mode((window_width,window_height))pygame.display.set_caption("雷霆战机")#加载图片player_img=
JS笔记
陈两全
笔记
9.111.Math对象Math对象属于Javascript内置对象,无需实例化(不需要添加new),可以直接使用。只有一个Math.PI的属性1.1.Math对象的方法Math.round(number)//四舍五入整数Math.ceil(number)//向上取整Math.floor(number)//向下取整Math.random()//随机返回0.0~1.0之间的数Math.max(x,y
极简之美:探索Minimal Linux Live的开源之旅
芮妍娉Keaton
极简之美:探索MinimalLinuxLive的开源之旅minimalMinimalLinuxLive(MLL)isatinyeducationalLinuxdistribution,whichisdesignedtobebuiltfromscratchbyusingacollectionofautomatedshellscripts.MinimalLinuxLiveoffersacoreenvi
[学习笔记]《CSAPP》深入理解计算机系统 - Chapter 6 存储器层次结构
Artintel
学习学习笔记ccsapp
总结一些第六章的一些关键信息Chapter6存储器层次结构DMA局部性抖动Chapter6存储器层次结构随机访问存储器(Random-AccessMemory,RAM)分为两类:静态的和动态的。静态(SRAM)比动态更快,更贵动态(DRAM)数据流通过称为总线(bus)的共享电子电路在处理器和DRAM主存来来回回。每次CPU和主存之间的数据传送都是通过一系列的步骤来完成的,这些步骤称为总线事务(b
js实现动态生成不固定数量的气泡
小丁冲鸭!
javascript前端开发语言
样式:核心代码:1、添加气泡的方法addCircle(){letheight=645;letwidth=312;letminSize=38;letmaxSize=78;letnewCircle={x:Math.random()*width,//随机位置,留出边界y:Math.random()*height,size:(minSize+Math.random()*(maxSize-minSize+1
膨胀腐蚀操作opencv dilate膨胀白膨胀,erode腐蚀是黑吃白。主要针对二值图
tony365
opencv人工智能计算机视觉
效果:代码:importcv2importnumpyasnpfrommatplotlibimportpyplotaspltif__name__=="__main__":h=10w=10data=np.random.normal(0,1,[h,w])#sigma,2*sigma,3*sigma之间的数的比例分别为0.68,0.96,0.99mask_new=data>2print(data)prin
蒙特卡罗——三门问题python代码实现
潮汐退涨月冷风霜
python开发语言蒙特卡罗
三门问题b站李永乐老师讲解三门问题python蒙特卡罗模拟#模拟三门问题importrandomasrd#n:模拟次数,m:中奖次数n=100000m=0foriinrange(n):#车位于的门号car=rd.randint(0,2)#人随机选择一个门door=rd.randint(0,2)#主持人展示空门empties={0,1,2}-{car,door}empty=rd.choice(lis
python爬虫处理滑块验证_python selenium爬虫滑块验证
用户6731453637
python爬虫处理滑块验证
importrandomimporttimefromPILimportImagefromioimportBytesIOimportrequestsasrqfrombs4importBeautifulSoupasbsfromseleniumimportwebdriverfromselenium.webdriverimportActionChainsfromselenium.webdriverimpo
Matlab 简单计算PDF和CDF
奔跑着的孩子
通信概念最大似然算法
CDF(cumulativedistributionfunction)叫做累积分布函数,描述一个实数随机变量X的概率分布,是概率密度函数的积分。它的最主要作用就是观测某些数值也就是随机变量的取值在那个附近出现的概率比较大,它是一个增函数.可以有效的处理一些异常值.随机变量小于或者等于某个数值的概率P(X=b(i)&a(s)<=b(i+1)n(i)=n(i)+1;s=s+1;endendendsum
Python代码雨
镜花照无眠
#Python
importrandomimportpygameimportsys#初始化参数设计win_width=1000win_height=800font_px=15#创建窗口及文本设计pygame.init()winsur=pygame.display.set_mode((win_width,win_height))font=pygame.font.SysFont('',23)bg_surface=py
CentOS 7 上安装 NVIDIA Docker
ManchiBB
centosdockerlinux
在CentOS7上安装NVIDIADocker需要几个步骤。以下是安装NVIDIADocker的基本步骤:安装NVIDIA驱动:确保您的系统已经安装了NVIDIA驱动。如果没有,请先安装驱动。添加NVIDIADocker仓库:添加NVIDIADocker的官方仓库,以便安装最新版本的NVIDIADocker。distribution=$(./etc/os-release;echo$ID$VERSI
蒙特卡罗方法——布丰投针实验近似计算圆周率python代码实现
潮汐退涨月冷风霜
python开发语言蒙特卡罗
布丰实验数学原理python代码importrandomasrdimportnumpyasnpimportmathimportmatplotlib.pyplotaspltimportmatplotlibmatplotlib.rcParams['font.family']='SimHei'#或者'MicrosoftYaHei'matplotlib.rcParams['axes.unicode_min
Day05for和while
PythonLi
1.如果是不断的获取序列中的元素,直接使用for循环2.如果循环次数确定,最好也使用for循环3.死循环和循环次数不确定的时候最好使用while循环。练习:随机产生一个数字(0,100),不断的输入数字,直到输入的数字和产生的随机数相同为止如果猜错了提示大了或者小importrandom产生一个随机数number=random.randint(0,100)返回从键盘接受到的数据(输入的时候以回车结
存储器相关问题
远行者223
FPGAlearining缓存
存储器、硬件相关问题FPGA探索者题型总结1.存储器1.1分类ROM只读存储器Read-OnlyMemoryRAM随机存取存储器RandomAccessMemorySRAM静态随机存取存储器StaticRandom-AccessMemoryDRAM动态随机存取存储器DynamicRandomAccessMemorySDRAM同步动态随机存取内存SynchronousDynamicRandom-ac
ztree设置禁用节点
3213213333332132
JavaScriptztreejsonsetDisabledNodeAjax
ztree设置禁用节点的时候注意,当使用ajax后台请求数据,必须要设置为同步获取数据,否者会获取不到节点对象,导致设置禁用没有效果。
$(function(){
showTree();
setDisabledNode();
});
JVM patch by Taobao
bookjovi
javaHotSpot
在网上无意中看到淘宝提交的hotspot patch,共四个,有意思,记录一下。
7050685:jsdbproc64.sh has a typo in the package name
7058036:FieldsAllocationStyle=2 does not work in 32-bit VM
7060619:C1 should respect inline and
将session存储到数据库中
dcj3sjt126com
sqlPHPsession
CREATE TABLE sessions (
id CHAR(32) NOT NULL,
data TEXT,
last_accessed TIMESTAMP NOT NULL,
PRIMARY KEY (id)
);
<?php
/**
* Created by PhpStorm.
* User: michaeldu
* Date
Vector
171815164
vector
public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) {
for (int i = 0; i < cart.size(); i++) {
if (cart.get(i).getId().equals(id)) {
cart.remove(i);
各连接池配置参数比较
g21121
连接池
排版真心费劲,大家凑合看下吧,见谅~
Druid
DBCP
C3P0
Proxool
数据库用户名称 Username Username User
数据库密码 Password Password Password
驱动名
[简单]mybatis insert语句添加动态字段
53873039oycg
mybatis
mysql数据库,id自增,配置如下:
<insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id"
parameterType=&
struts2拦截器配置
云端月影
struts2拦截器
struts2拦截器interceptor的三种配置方法
方法1. 普通配置法
<struts>
<package name="struts2" extends="struts-default">
&
IE中页面不居中,火狐谷歌等正常
aijuans
IE中页面不居中
问题是首页在火狐、谷歌、所有IE中正常显示,列表页的页面在火狐谷歌中正常,在IE6、7、8中都不中,觉得可能那个地方设置的让IE系列都不认识,仔细查看后发现,列表页中没写HTML模板部分没有添加DTD定义,就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
String,int,Integer,char 几个类型常见转换
antonyup_2006
htmlsql.net
如何将字串 String 转换成整数 int?
int i = Integer.valueOf(my_str).intValue();
int i=Integer.parseInt(str);
如何将字串 String 转换成Integer ?
Integer integer=Integer.valueOf(str);
如何将整数 int 转换成字串 String ?
1.
PL/SQL的游标类型
百合不是茶
显示游标(静态游标)隐式游标游标的更新和删除%rowtyperef游标(动态游标)
游标是oracle中的一个结果集,用于存放查询的结果;
PL/SQL中游标的声明;
1,声明游标
2,打开游标(默认是关闭的);
3,提取数据
4,关闭游标
注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标
隐式游标:主要是对DML数据的操作隐
JUnit4中@AfterClass @BeforeClass @after @before的区别对比
bijian1013
JUnit4单元测试
一.基础知识
JUnit4使用Java5中的注解(annotation),以下是JUnit4常用的几个annotation: @Before:初始化方法 对于每一个测试方法都要执行一次(注意与BeforeClass区别,后者是对于所有方法执行一次)@After:释放资源 对于每一个测试方法都要执行一次(注意与AfterClass区别,后者是对于所有方法执行一次
精通Oracle10编程SQL(12)开发包
bijian1013
oracle数据库plsql
/*
*开发包
*包用于逻辑组合相关的PL/SQL类型(例如TABLE类型和RECORD类型)、PL/SQL项(例如游标和游标变量)和PL/SQL子程序(例如过程和函数)
*/
--包用于逻辑组合相关的PL/SQL类型、项和子程序,它由包规范和包体两部分组成
--建立包规范:包规范实际是包与应用程序之间的接口,它用于定义包的公用组件,包括常量、变量、游标、过程和函数等
--在包规
【EhCache二】ehcache.xml配置详解
bit1129
ehcache.xml
在ehcache官网上找了多次,终于找到ehcache.xml配置元素和属性的含义说明文档了,这个文档包含在ehcache.xml的注释中!
ehcache.xml : http://ehcache.org/ehcache.xml
ehcache.xsd : http://ehcache.org/ehcache.xsd
ehcache配置文件的根元素是ehcahe
ehcac
java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL
白糖_
javaeclipsespringtomcatWeb
今天学习spring+cxf的时候遇到一个问题:在web.xml中配置了spring的上下文监听器:
<listener>
<listener-class>org.springframework.web.context.ContextLoaderListener</listener-class>
</listener>
随后启动
angular.element
boyitech
AngularJSAngularJS APIangular.element
angular.element
描述: 包裹着一部分DOM element或者是HTML字符串,把它作为一个jQuery元素来处理。(类似于jQuery的选择器啦) 如果jQuery被引入了,则angular.element就可以看作是jQuery选择器,选择的对象可以使用jQuery的函数;如果jQuery不可用,angular.e
java-给定两个已排序序列,找出共同的元素。
bylijinnan
java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class CommonItemInTwoSortedArray {
/**
* 题目:给定两个已排序序列,找出共同的元素。
* 1.定义两个指针分别指向序列的开始。
* 如果指向的两个元素
sftp 异常,有遇到的吗?求解
Chen.H
javajcraftauthjschjschexception
com.jcraft.jsch.JSchException: Auth cancel
at com.jcraft.jsch.Session.connect(Session.java:460)
at com.jcraft.jsch.Session.connect(Session.java:154)
at cn.vivame.util.ftp.SftpServerAccess.connec
[生物智能与人工智能]神经元中的电化学结构代表什么?
comsci
人工智能
我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色....
我们可以尝试一下...在某些神经
通过LAC和CID获取经纬度信息
dai_lm
laccid
方法1:
用浏览器打开http://www.minigps.net/cellsearch.html,然后输入lac和cid信息(mcc和mnc可以填0),如果数据正确就可以获得相应的经纬度
方法2:
发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
JAVA的困难分析
datamachine
java
前段时间转了一篇SQL的文章(http://datamachine.iteye.com/blog/1971896),文章不复杂,但思想深刻,就顺便思考了一下java的不足,当砖头丢出来,希望引点和田玉。
-----------------------------------------------------------------------------------------
小学5年级英语单词背诵第二课
dcj3sjt126com
englishword
money 钱
paper 纸
speak 讲,说
tell 告诉
remember 记得,想起
knock 敲,击,打
question 问题
number 数字,号码
learn 学会,学习
street 街道
carry 搬运,携带
send 发送,邮寄,发射
must 必须
light 灯,光线,轻的
front
linux下面没有tree命令
dcj3sjt126com
linux
centos p安装
yum -y install tree
mac os安装
brew install tree
首先来看tree的用法
tree 中文解释:tree
功能说明:以树状图列出目录的内容。
语 法:tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
Map迭代方式,Map迭代,Map循环
蕃薯耀
Map循环Map迭代Map迭代方式
Map迭代方式,Map迭代,Map循环
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年
Spring Cache注解+Redis
hanqunfeng
spring
Spring3.1 Cache注解
依赖jar包:
<!-- redis -->
<dependency>
<groupId>org.springframework.data</groupId>
<artifactId>spring-data-redis</artifactId>
Guava中针对集合的 filter和过滤功能
jackyrong
filter
在guava库中,自带了过滤器(filter)的功能,可以用来对collection 进行过滤,先看例子:
@Test
public void whenFilterWithIterables_thenFiltered() {
List<String> names = Lists.newArrayList("John"
学习编程那点事
lampcy
编程androidPHPhtml5
一年前的夏天,我还在纠结要不要改行,要不要去学php?能学到真本事吗?改行能成功吗?太多的问题,我终于不顾一切,下定决心,辞去了工作,来到传说中的帝都。老师给的乘车方式还算有效,很顺利的就到了学校,赶巧了,正好学校搬到了新校区。先安顿了下来,过了个轻松的周末,第一次到帝都,逛逛吧!
接下来的周一,是我噩梦的开始,学习内容对我这个零基础的人来说,除了勉强完成老师布置的作业外,我已经没有时间和精力去
架构师之流处理---------bytebuffer的mark,limit和flip
nannan408
ByteBuffer
1.前言。
如题,limit其实就是可以读取的字节长度的意思,flip是清空的意思,mark是标记的意思 。
2.例子.
例子代码:
String str = "helloWorld";
ByteBuffer buff = ByteBuffer.wrap(str.getBytes());
Sy
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1
Everyday都不同
$转义el表达式
最近在做Highcharts的过程中,在写js时,出现了以下异常:
严重: Servlet.service() for servlet jsp threw exception
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
用Java实现发送邮件到163
tntxia
java实现
/*
在java版经常看到有人问如何用javamail发送邮件?如何接收邮件?如何访问多个文件夹等。问题零散,而历史的回复早已经淹没在问题的海洋之中。
本人之前所做过一个java项目,其中包含有WebMail功能,当初为用java实现而对javamail摸索了一段时间,总算有点收获。看到论坛中的经常有此方面的问题,因此把我的一些经验帖出来,希望对大家有些帮助。
此篇仅介绍用
探索实体类存在的真正意义
java小叶檀
POJO
一. 实体类简述
实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口,在程序中仅作为数据容器用来持久化存储数据用的
POJO(Plain Old Java Objects)简单的Java对象
它的一般格式就是
public class A{
private String id;
public Str
![]()
![]()
![]()
![]() ,
,![]()