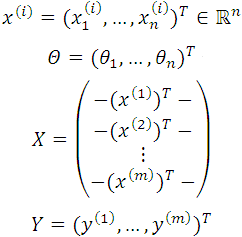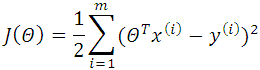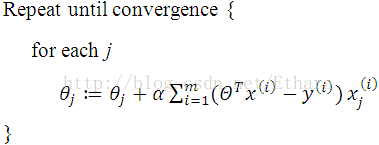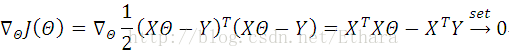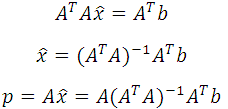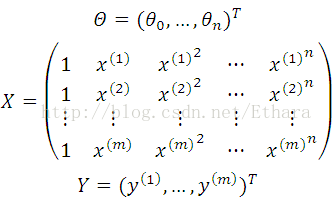Polynomial Curve Fitting

Polynomial Curve Fitting

Ethara

Polynomial curve fitting problem is such that, in a two dimensional plane, given a set of m sample points,

Figure 1

you are asked to fit them into an n-order polynomial curve in an analytical form,

How are we supposed to solve this problem with the sum of error squared to be minimized?

Let’s consider a more general problem where

Therefore, the problem is extended to solving the following equation for theta,

However, there is actually no solution. We can only find the best solution to the m equations with n unknowns by minimizing the cost function measuring how close the polynomial curve is to the sample points,

You may recognize this as the familiar least-squares cost function that gives rise to the ordinary least squares regression model.

We want to choose theta so as to minimize J(.). To do so, we can use a search algorithm called the gradient descent algorithm which starts with some initial theta and repeatedly performs the update:

Indeed, the gradient descent algorithm always works since J(.) is a convex quadratic function.

In fact, we can solve for theta in closed form by performing minimization explicitly and without resorting to an iterative algorithm. There are actually two straightforward ways to get this done.

In the first way, we minimize J by explicitly taking derivatives with respect to theta and setting them to zero.

Hence,

Then, we obtain the normal equations,

Thus, the value of theta that minimizes J(.) is given in closed form by equation,

Alternatively, in the second way, we will solve for theta using the projection matrix.

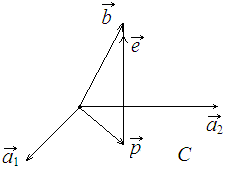
For the sake of intuition, let me derive the projection matrix in the three-dimensional space.

Figure 2

As shown in Figure 2,

By designing an orthogonal matrix,

you are to find x s.t. Ax = b.There’s actually no solution, either. But we can find the best solution by solving

Note that, e is perpendicular to Plane C, i.e.,

Further,

Let

P is called the projection matrix, which projects b onto Plane C. Likewise, this theory can be extended into the n-dimensional space.

Back to our problem, we can similarly project Y onto the space of X, and then the projection p is

Thus,we can solve

for theta,

This result is exactly the same with that of the first way.

Now we are able to solve the polynomial curve fitting problem where

by designing matrices,

So the polynomial curve fitting problem is to solve the equation

for theta

Postscript

Before this discussion, I had a misconception that least squares can only be utilized to solve the linear regression. As a matter of fact, however, it is so powerful that it is capable of solving the polynomial regression as well by designing some particular matrices.

Acknowledgement

This discussion benefits highly from the machine learning course of Stanford University and the linear algebra course of Massachusetts Institute of Technology.