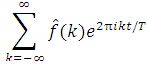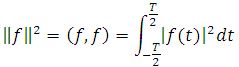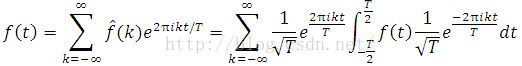Fourier Series
Fourier Series
Ethara
This work will present the derivation on Fourier series and give an intuitive understanding of it.
Derivation on Fourier Series
Given a periodic function f(t) with period T for all t, i.e., f(t) = f(t+T), we will reconstruct f(t) using fundamental periodic (harmonic) signals sin(.) and cos(.). One bold idea is to fill one period T with many (infinite later) frequencies among which 1/T is the smallest (See popular cartoons available from Internet as shown below), since the whole pattern cannot repeat until the longest pattern corresponding to the smallest frequency 1/T repeats.
To model an arbitrarily complicated signal f(t), we can modify amplitude, frequency and phase to the multivariate signal of period T with many frequencies,
Since
by adding a constant term, the multivariate signal becomes
Alternatively, to get a more compact form, representing sine and cosine via complex exponentials (Euler’s formula),
we can convert the trigonometric sum as above into
where Ck’s are complex numbers with symmetry property. (See Appendix I)
So, given a periodic function f(t) of period T, can we write the following equality (*)?
Suppose we can, then Ck’s are (See the proof in Appendix II)
where Ck’s are defined as Fourier coefficients.
Nevertheless, f(t) is not assured to be a continuous and infinitely differentiable function, which takes more higher frequencies to take sharp corners. Therefore, to represent the general periodic phenomena (signals), we have to consider infinite sum, i.e.,
Any non-smooth phenomenon signal will generate infinite many Fourier coefficients. Thus, we have to deal with issues of convergence. (which is set aside for the time being, since it is an exceedingly complicate mathematical problem)
Intuitive Understanding
What is Fourier series telling us?
Firstly, we define the inner product between two functions. If f(.) and g(.) are both squared integrable on [-T/2, T/2], the functional inner product is defined as
The squared norm of a real-valued function is
Moreover, f and g are orthogonal if (f, g) = 0.
Noting the mathematical fact that
we can find an infinite-dimensional orthonormal basis,
One projection of f(t) onto the k’th component of the basis is
Therefore, the intuitive conclusion is that, Fourier series is the sum of all the projections, that is, a function periodic of T is comprised of all its projections onto one component in the infinite-dimensional orthonormal basis,
Appendix
I. Ck’s are complex numbers with symmetry property,
where C0 is real. Why is the equality (*) a summation over k evaluated at from –n to n? The reason is to cancel the imaginary part. Here is the proof. Suppose Ck = ak + ibk, we have,
Therefore,
There is no imaginary part in (*), which assures each component in the summation is valid, since f(t) is a real-valued function.
II. Prove
Proof:
Since
Isolating the term with Cm,
Integrating both sides from –T/2 toT/2,
Therefore,
