POJ 2774 : Long Long Message (后缀数组)
原文: http://blog.sina.com.cn/s/blog_6635898a0102duef.html
题意:给定两个字符串 A 和 B ,求最长公共子串。
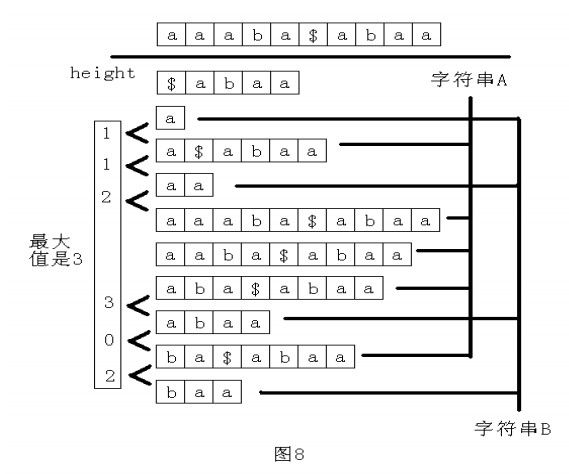
思路:后缀数组。(摘自罗穗骞的国家集训队论文)字符串的任何一个子串都是这个字符串的某个后缀的前缀。求 A 和 B的最长公共子串等价于求 A 的后缀和 B 的后缀的最长公共前缀的最大值。如果枚举A和 B的所有的后缀,那么这样做显然效率低下。由于要计算 A 的后缀和 B的后缀的最长公共前缀,所以先将第二个字符串写在第一个字符串后面,中间用一个没有出现过的字符隔开,再求这个新的字符串的后缀数组。观察一下,看看能不能从这个新的字符串的后缀数组中找到一些规律。以A=“ aaaba ”,B=“ abaa ”为例,如图 8 所示。
那么是不是所有的 height值中的最大值就是答案呢?不一定!有可能这两个后缀是在同一个字符串中的,所以实际上只有当suffix(sa[i-1])和suffix(sa[i])不是同一个字符串中的两个后缀时,height[i]才是满足条件的。而这其中的最大值就是答案。记字符串 A 和字符串 B的长度分别为|A|和|B|。求新的字符串的后缀数组和 height 数组的时间是 O(|A|+|B|) ,然后求排名相邻但原来不在同一个字符串中的两个后缀的height值的最大值,时间也是O(|A|+|B|),所以整个做法的时间复杂度为O(|A|+|B|) 。时间复杂度已经取到下限,由此看出,这是一个非常优秀的算法。
源代码:(5676K,313MS)
#include<iostream>
#include<cstring>
#define max(a,b) ((a)>(b)?(a):(b))
using namespace std;
const int MAX = 200050;
int sa[MAX], rank[MAX], height[MAX];
int wa[MAX], wb[MAX], wv[MAX], wd[MAX];
int cmp(int *r, int a, int b, int l)
{
return r[a] == r[b]&& r[a+l] == r[b+l];
}
void da(int *r, int n, int m) // 倍增算法0(nlgn)。
{
int i, j, p, *x = wa, *y= wb, *t;
for(i = 0; i< m; i ++) wd[i] = 0;
for(i = 0; i< n; i ++) wd[x[i]=r[i]] ++;
for(i = 1; i< m; i ++) wd[i] += wd[i-1];
for(i = n-1; i>= 0; i --) sa[-- wd[x[i]]] = i;
for(j = 1, p = 1; p< n; j *= 2, m = p)
{
for(p = 0, i = n-j; i < n; i ++)y[p ++] = i;
for(i = 0; i < n; i ++) if(sa[i]>= j) y[p ++] = sa[i] - j;
for(i = 0; i < n; i ++) wv[i] =x[y[i]];
for(i = 0; i < m; i ++) wd[i] =0;
for(i = 0; i < n; i ++) wd[wv[i]]++;
for(i = 1; i < m; i ++) wd[i] +=wd[i-1];
for(i = n-1; i >= 0; i --) sa[--wd[wv[i]]] = y[i];
for(t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i= 1; i < n; i ++)
{
x[sa[i]] =cmp(y, sa[i-1], sa[i], j) ? p - 1 : p ++;
}
}
}
void calHeight(int *r, int n) // 求height数组。
{
int i, j, k = 0;
for(i = 1; i<= n; i ++) rank[sa[i]] = i;
for(i = 0; i< n; height[rank[i ++]] = k)
{
for(k ? k -- : 0, j = sa[rank[i]-1]; r[i+k] ==r[j+k]; k ++);
}
}
int main()
{
int i, k, l1, l2,num[MAX];
char str[MAX];
scanf("%s", str);
l1 = strlen(str);
for(k = i = 0; i< l1; i ++)
{
num[k ++] = str[i] - 'a' + 2;
}
num[k ++] = 1; // 相当于论文中的'$'分隔符。
scanf("%s", str);
l2 = strlen(str);
for(i = 0; i< l2; i ++)
{
num[k ++] = str[i] - 'a' + 2;
}
int n = l1 + l2;
da(num, n + 1,30);
calHeight(num, n);
int ans = 0;
for(i = 2; i< k; i ++)
if((sa[i] < l1&& sa[i-1] > l1) ||(sa[i-1] < l1 &&sa[i] > l1))
{
ans =max(ans, height[i]);
}
printf("%d\n",ans);
return 0;
}
=================================有时间解决下========================================
我写的一个求公共字串的算法:就是两个循环。有待利用后缀数组的概念改进
#include <stdio.h>
#include <string.h>
#include <malloc.h>
char *maxcommstr(char *str1, char *str2)
{
char *commstr; // 返回最大公共字串
char *tmpcomstr1, *tmpcomstr2;
char *p1, *p2, *p3, *p4;
int len;
// 有一个串为空,则返回NULL
if(str1 == NULL || str2 == NULL)
return NULL;
// p1 指向最长的串
if(strlen(str1) >= strlen(str2)){
p1 = str1;
p2 = str2;
}else{
p1 = str2;
p2 = str1;
}
//
commstr = malloc(256);
tmpcomstr1 = malloc(256);
tmpcomstr2 = malloc(256);
memset(commstr , '\0', sizeof(commstr));
memset(tmpcomstr1, '\0', sizeof(tmpcomstr1));
memset(tmpcomstr2, '\0', sizeof(tmpcomstr2));
while(*p1 != '\0'){
p3 = p1;
p4 = p2;
len = 0;
while(*p4 != '\0'){
if(*p4 == *p3){
tmpcomstr1[len++] = *p4;
p3++;
}else if(len > 0){ // 此公共串结束
tmpcomstr1[len] = '\0';
p3 = p1; // 恢复p3
len = 0;
// tmpcomstr2 <-- max(tmpcomstr1, tmpcomstr2)
if(strlen(tmpcomstr1) > strlen(tmpcomstr2)){
strcpy(tmpcomstr2, tmpcomstr1);
}
}
p4++;
}
// tmpcomstr2 <-- max(tmpcomstr1, tmpcomstr2)
if(strlen(tmpcomstr1) > strlen(tmpcomstr2)){
strcpy(tmpcomstr2, tmpcomstr1);
}
// commstr <-- max(commstr, tmpcomstr2)
if(strlen(tmpcomstr2) > strlen(commstr)){
strcpy(commstr, tmpcomstr2);
}
memset(tmpcomstr1, '\0', sizeof(tmpcomstr1));
memset(tmpcomstr2, '\0', sizeof(tmpcomstr2));
p1++;
}
//free
free(tmpcomstr1);
free(tmpcomstr2);
return commstr;
}
int main()
{
printf("%s\n", maxcommstr("gbafezzzzz", "dafgaf"));
return 0;
}
======================================关于本问题的其它博文============================================
http://blog.csdn.net/ysjjovo/article/details/6635138
==========================================13-6-19=========================================================
原文: http://hi.baidu.com/ahnkftravhdhkyr/item/021db59784502d15924f41f1
学习了后缀数组之后,很容易就解决这个问题。
AC的代码:
Source Code
| Problem: 2774 | User: huntinux | |
| Memory: 5792K | Time: 344MS | |
| Language: C | Result: Accepted |
- Source Code
#include <stdio.h> #include <string.h> #define maxn 100000*2+1+1 int wa[maxn],wb[maxn],wv[maxn],ws[maxn]; int cmp(int *r,int a,int b,int l) {return r[a]==r[b]&&r[a+l]==r[b+l];} //就像论文所说,由于末尾填了0,所以如果r[a]==r[b](实际是y[a]==y[b]),说明待合并的两个长为j的字符串,前面那个一定不包含末尾0,因而后面这个的起始位置至多在0的位置,不会再靠后了,因而不会产生数组越界。 //da函数的参数n代表字符串中字符的个数,这里的n里面是包括人为在字符串末尾添加的那个0的,但论文的图示上并没有画出字符串末尾的0。 //da函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值。 void da(int *r,int *sa,int n,int m) { int i,j,p,*x=wa,*y=wb,*t; //以下四行代码是把各个字符(也即长度为1的字符串)进行基数排序,如果不理解为什么这样可以达到基数排序的效果,不妨自己实际用纸笔模拟一下,我最初也是这样才理解的。(chj联想到计数排序) for(i=0;i<m;i++) ws[i]=0; for(i=0;i<n;i++) ws[x[i]=r[i]]++; //x[]里面本意是保存各个后缀的rank值的,但是这里并没有去存储rank值,因为后续只是涉及x[]的比较工作,因而这一步可以不用存储真实的rank值,能够反映相对的大小即可。 for(i=1;i<m;i++) ws[i]+=ws[i-1]; for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i; //i之所以从n-1开始循环,是为了保证在当字符串中有相等的字符串时,默认靠前的字符串更小一些。 //下面这层循环中p代表rank值不用的字符串的数量,如果p达到n,那么各个字符串的大小关系就已经明了了。 //j代表当前待合并的字符串的长度,每次将两个长度为j的字符串合并成一个长度为2*j的字符串,当然如果包含字符串末尾具体则数值应另当别论,但思想是一样的。 //m同样代表基数排序的元素的取值范围 for(j=1,p=1;p<n;j*=2,m=p) { //以下两行代码实现了对第二关键字的排序 for(p=0,i=n-j;i<n;i++) y[p++]=i; //结合论文的插图,我们可以看到位置在第n-j至n的元素的第二关键字都为0,因此如果按第二关键字排序,必然这些元素都是排在前面的。 for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j; //结合论文的插图,我们可以看到,下面一行的第二关键字不为0的部分都是根据上面一行的排序结果得到的,且上一行中只有sa[i]>=j的第sa[i]个字符串(这里以及后面指的“第?个字符串”不是按字典序排名来的,是按照首字符在字符串中的位置来的)的rank才会作为下一行的第sa[i]-j个字符串的第二关键字,而且显然按sa[i]的顺序rank[sa[i]]是递增的,因此完成了对剩余的元素的第二关键字的排序。 //第二关键字基数排序完成后,y[]里存放的是按第二关键字排序的字符串下标 for(i=0;i<n;i++) wv[i]=x[y[i]]; //这里相当于提取出每个字符串的第一关键字(前面说过了x[]是保存rank值的,也就是字符串的第一关键字),放到wv[]里面是方便后面的使用 //以下四行代码是按第一关键字进行的基数排序 for(i=0;i<m;i++) ws[i]=0; for(i=0;i<n;i++) ws[wv[i]]++; for(i=1;i<m;i++) ws[i]+=ws[i-1]; for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i]; //i之所以从n-1开始循环,含义同上,同时注意这里是y[i],因为y[i]里面才存着字符串的下标 //下面两行就是计算合并之后的rank值了,而合并之后的rank值应该存在x[]里面,但我们计算的时候又必须用到上一层的rank值,也就是现在x[]里面放的东西,如果我既要从x[]里面拿,又要向x[]里面放,怎么办?当然是先把x[]的东西放到另外一个数组里面,省得乱了。这里就是用交换指针的方式,高效实现了将x[]的东西“复制”到了y[]中。 for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //这里就是用x[]存储计算出的各字符串rank的值了,记得我们前面说过,计算sa[]值的时候如果字符串相同是默认前面的更小的,但这里计算rank的时候必须将相同的字符串看作有相同的rank,要不然p==n之后就不会再循环啦。 } return; } //能够线性计算height[]的值的关键在于h[](height[rank[]])的性质,即h[i]>=h[i-1]-1,下面具体分析一下这个不等式的由来。 //论文里面证明的部分一开始看得我云里雾里,后来画了一下终于搞明白了,我们先把要证什么放在这:对于第i个后缀,设j=sa[rank[i] - 1],也就是说j是i的按排名来的上一个字符串,按定义来i和j的最长公共前缀就是height[rank[i]],我们现在就是想知道height[rank[i]]至少是多少,而我们要证明的就是至少是height[rank[i-1]]-1。 //好啦,现在开始证吧。 //首先我们不妨设第i-1个字符串(这里以及后面指的“第?个字符串”不是按字典序排名来的,是按照首字符在字符串中的位置来的)按字典序排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2,因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。 //这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀自然是height[rank[i-1]],现在先讨论一下第k+1个字符串和第i个字符串的关系。 //第一种情况,第k个字符串和第i-1个字符串的首字符不同,那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面,但没有关系,因为height[rank[i-1]]就是0了呀,那么无论height[rank[i]]是多少都会有height[rank[i]]>=height[rank[i-1]]-1,也就是h[i]>=h[i-1]-1。 //第二种情况,第k个字符串和第i-1个字符串的首字符相同,那么由于第k+1个字符串就是第k个字符串去掉首字符得到的,第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然第k+1个字符串要排在第i个字符串前面,要么就产生矛盾了。同时,第k个字符串和第i-1个字符串的最长公共前缀是height[rank[i-1]],那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rank[i-1]]-1。 //到此为止,第二种情况的证明还没有完,我们可以试想一下,对于比第i个字符串的字典序排名更靠前的那些字符串,谁和第i个字符串的相似度最高(这里说的相似度是指最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀,即sa[rank[i]-1]。也就是说sa[rank[i]]和sa[rank[i]-1]的最长公共前缀至少是height[rank[i-1]]-1,那么就有height[rank[i]]>=height[rank[i-1]]-1,也即h[i]>=h[i-1]-1。 //证明完这些之后,下面的代码也就比较容易看懂了。 int rank[maxn],height[maxn]; void calheight(int *r,int *sa,int n) { int i,j,k=0; for(i=1;i<=n;i++) rank[sa[i]]=i; //计算每个字符串的字典序排名 for(i=0;i<n;height[rank[i++]]=k) //将计算出来的height[rank[i]]的值,也就是k,赋给height[rank[i]]。i是由0循环到n-1,但实际上height[]计算的顺序是由height[rank[0]]计算到height[rank[n-1]]。 for(k?k--:0,j=sa[rank[i]-1];r[i+k]==r[j+k];k++); //上一次的计算结果是k,首先判断一下如果k是0的话,那么k就不用动了,从首字符开始看第i个字符串和第j个字符串前面有多少是相同的,如果k不为0,按我们前面证明的,最长公共前缀的长度至少是k-1,于是从首字符后面k-1个字符开始检查起即可。 return; } int nstr1, nstr2; int check(int a,int b){ if (a>b) return check(b,a); if (a<nstr1&&b>nstr1) return 1;//一开始我写成(a-n1)*(b-n1)<0,为什么会不对呢..求高手指点! else return 0; } int main() { //最后再说明一点,就是关于da和calheight的调用问题,实际上在“小罗”写的源程序里面是如下调用的,这样我们也能清晰的看到da和calheight中的int n不是一个概念,同时height数组的值的有效范围是height[1]~height[n]其中height[1]=0,原因就是sa[0]实际上就是我们补的那个0,所以sa[1]和sa[0]的最长公共前缀自然是0。 char arr[maxn]; int r[maxn]; int i; int n; int sa[maxn]; int max_height; // 读入字符串用 '@' 连接 scanf("%s", arr); nstr1 = strlen(arr); arr[nstr1] = '@'; scanf("%s", arr + nstr1 + 1); nstr2 = strlen(arr + nstr1 + 1); // 求后缀数组, heigth[] n = strlen(arr); for(i = 0; i < n; i++) r[i] = arr[i]; da(r,sa,n+1,128); calheight(r,sa,n); // 找到height[]中最大数字即可 max_height = 0; for(i = 2; i <= n; i++) if(check(sa[i-1], sa[i]) && max_height < height[i]) max_height = height[i]; printf("%d\n", max_height); return 0; }
int check(int a,int b){ if (a>b) return check(b,a); if (a<nstr1&&b>nstr1) return 1;//一开始我写成(a-n1)*(b-n1)<0,为什么会不对呢..求高手指点! else return 0; }