POJ 2486 Apple Tree
学习树形DP时间不是很长,之前做的都是没有考虑返回这种情况。
现在要考虑一个节点会不会返回,增加一维表示该点是不是返回。
借鉴文章
dp[i][i][0]表示从i出发走j步回到i的可以得到的最大价值
dp[i][i][0]表示从i出发走j步不回到i的可以得到的最大价值
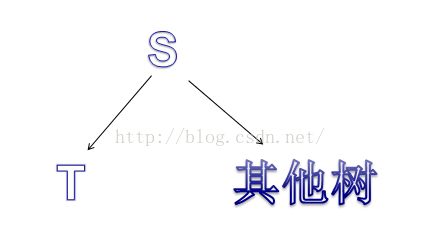
现在有三种措施:要么去s的其他子树呆着,要么去t子树呆着,要么回到s点
1、返回S 那么T就要返回S(dp[t][k][0]),其他子树返回也要返回S点(dp[s][j-k][0])
2、去其他子树 那么T返回到S点(dp[t][k][0]),从S到其他子树不返回(dp[s][j-k][1]);
3、S去T子树不返回 (dp[s][k][1]) 其他子树返回到S点(dp[s][j-k][0] );
1、dp[s][j+2][0]=max(dp[s][j+2][0],dp[s][j-k][0]+dp[t][k][0]);//S-T,T-S(T返回)花两步
2、dp[s][j+2][1]=max(dp[s][j+2][1],dp[s][j-k][1]+dp[t][k][0]);//去其他树 也要从T-S ,S-T,两步
3、dp[s][j+1][1]=max(dp[s][j+1][1],dp[s]j-k][0]+dp[t][k][1]);//去T不返回 只需要走一遍s-t所以加+1
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int N=202;
int dp[N][N][2];
int n,m;
int pnt[N],nxt[N],head[N],e=0;
int val[N];
void AddEdge(int u,int v)
{
pnt[e]=v;nxt[e]=head[u];head[u]=e++;
}
void dfs(int u,int fa)
{
for(int i=head[u];i!=-1;i=nxt[i])
{
int v=pnt[i];
if(v!=fa){
dfs(v,u);
int s=u,t=v;
for(int j=m;j>=0;j--)
for(int k=0;k<=j;k++)
{
dp[s][j+2][0]=max(dp[s][j+2][0],dp[s][j-k][0]+dp[t][k][0]);
dp[s][j+2][1]=max(dp[s][j+2][1],dp[s][j-k][1]+dp[t][k][0]);
dp[s][j+1][1]=max(dp[s][j+1][1],dp[s][j-k][0]+dp[t][k][1]);
}
}
}
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
memset(head,-1,sizeof(head));
e=0;
for(int i=1;i<=n;i++){
scanf("%d",&val[i]);
for(int j=0;j<=m;j++)
dp[i][j][0]=dp[i][j][1]=val[i];
}
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
AddEdge(u,v);
AddEdge(v,u);
}
dfs(1,-1);
printf("%d\n",dp[1][m][1]);
}
return 0;
}