剖析八种经典排序算法
排序(Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个关键字有序的序列。
我整理了以前自己所写的一些排序算法结合网上的一些资料,共介绍8种常用的排序算法,希望对大家能有所帮助。
八种排序算法分别是:
1.冒泡排序;
2.选择排序;
3.插入排序;
4.快速排序;
5.归并排序;
6.希尔排序;
7.二叉排序;
8.计数排序;
其中快排尤为重要,几乎可以说IT开发类面试必考内容,而希尔排序和归并排序的思想也非常重要。下面将各个排序算法的排序原理,代码实现和时间复杂度一一介绍。
—,最基础的排序——冒泡排序
冒泡排序是许多人最早接触的排序算法,由于逻辑简单,所以大量的出现在计算机基础课本上,作为一种最基本的排序算法被大家所熟知。
设无序数组a[]长度为N,以由小到大排序为例。冒泡的原理是这样的:
1.比较相邻的前两个数据,如果前面的数据a[0]大于后面的数据a[1] (为了稳定性,等于不交换),就将前面两个数据进行交换。在将计数器 i ++;
2.当遍历完N个数据一遍后,最大的数据就会沉底在数组最后a[N-1]。
3.然后N=N-1;再次进行遍历排序将第二大的数据沉到倒数第二位置上a[N-2]。再次重复,直到N=0;将所有数据排列完毕。
无序数组: 2 5 4 7 1 6 8 3
遍历1次后: 2 4 5 1 6 7 3 8
遍历2次后: 2 4 1 5 6 3 7 8
...
遍历7次后: 1 2 3 4 5 6 7 8 可以轻易的得出,冒泡在 N– 到 0 为止,每遍近似遍历了N个数据。所以冒泡的时间复杂度是 -O(N^2)。
按照定义实现代码如下:
void BubbleSore(int *array, int n)
{
int i = 0;
int j = 0;
int temp = 0;
for(i = 0; i < n; ++i){
for(j = 1; j < n - i; ++j){
if(array[j - 1] > array[j]){
temp = array[j-1];
array[j - 1] = array[j];
array[j] = temp;
}
}
}
}我们对可以对冒泡进行优化,循环时,当100个数据,仅前10个无序,发生了交换,后面没有交换说明有序且都大于前10个数据,那么以后循环遍历时,就不必对后面的90个数据进行遍历判断,只需每遍从0循环到10就行了。
void BubbleSore(int *array, int n) //优化
{
int i = n;
int j = 0;
int temp = 0;
Boolean flag = TRUE;
while(flag){
flag = FALSE;
for(j = 1; j < i; ++j){
if(array[j - 1] > array[j]){
temp = array[j-1];
array[j - 1] = array[j];
array[j] = temp;
flag = TRUE;
}
}
i--;
}
}虽然我们对冒泡进行了优化,但优化后的时间复杂度逻辑上还是-O(n^2),所以说冒泡还是效率比较低下的,数据较大时,建议不要采用冒泡。
二,最易理解的排序——选择排序
如果让一个初学者写一个排序算法,很有可能写出的就是选择排序(反正我当时就是 ^.^),因为选择排序甚至比冒泡更容易理解。
原理就是遍历一遍找到最小的,放在第一个位置。在遍历一遍找到第二小的,放在第二个位置。看起来比较像冒泡,但它不是相邻数据交换的。
无序数组: 2 5 4 7 1 6 8 3
遍历1次后: 1 2 5 4 7 6 8 3
遍历2次后: 1 2 5 4 7 6 8 3
...
遍历7次后: 1 2 3 4 5 6 7 8 选择排序的时间复杂度也是 -O(N^2);
void Selectsort(int *array, int n)
{
int i = 0;
int j = 0;
int min = 0;
int temp = 0;
for(i; i < n; i++){
min = i;
for(j = i + 1; j < n; j++){
if(array[min] > array[j])
min = j;
}
temp = array[min];
array[min] = array[i];
array[i] = temp;
}
}
#endif三,扑克牌法排序——插入排序
打牌时(以挖坑为例)我们一张张的摸牌,将摸到的牌插入手牌的”顺子”里,凑成更长的顺子,这就是插入排序的含义。
设无序数组a[]长度为N,以由小到大排序为例。插入的原理是这样的:
1.初始时,第一个数据a[0]自成有序数组,后面的a[1]~a[N-1]为无序数组。令 i = 1;
2.将第二个数据a[1]加入有序序列a[0]中,使a[0]~a[1]变为有序序列。i++;
3.重复循环第二步,直到将后面的所有无序数插入到前面的有序数列内,排序完成。
无序数组: 2 | 5 4 7 1 6 8 3
遍历1次后: 2 5 | 4 7 1 6 8 3
遍历2次后: 2 4 5 | 7 1 6 8 3
遍历3次后: 2 4 5 7 | 1 6 8 3
...插入排序的时间度仍然是-O(N^2),但是,插入排序是一种比较快的排序,因为它每次都是和有序的数列进行比较插入,所以每次的比较很有”意义”,导致交换次数较少,所以插入排序在-O(N^2)级别的排序中是比较快的排序算法。
{
int i = 0;
int j = 0;
int temp = 0;
for(i = 1; i < n; i++){
if(array[i] < array[i-1]){
temp = array[i];
for(j = i - 1; j >= 0 && array[j] > temp; j--){
array[j+1] = array[j];
}
array[j+1] = temp;
}
}
}四,最快的排序——快速排序
我真的很敬佩设计出这个算法的大神,连起名字都这么霸气——Quick Sort。为什么这么自信的叫快速排序?因为已经被数学家证明出 在交换类排序算法中,快排是是速度最快的!
快排是C.R.A.Hoare于1962年提出的一种划分交换区的排序。它采用一种很重要的”分治法(Divide-and-ConquerMethod)”的思想。快排是一种很有实用价值的排序方法,很多IT公司在面试算法时几乎都会去问,所以快排是一定要掌握的。
快排的原理是这样的:
1. 先在无序的数组中取出一个数作为基数。
2. 将比基数小的数扔到基数的左边,成为一个区。将比基数大的数扔到基数的右边,成为另一个区。
3. 将左右两个区重复进行前两步操作,使数列变成四个区。
4. 重复操作,直到每个区里只有一个数时,排序完成。
快速排序初次接触比较难理解,我们可以把快排看做挖坑填数,具体操作如下:
数组下标: 0 1 2 3 4 5 6 7
无序数列: 4 2 5 7 1 6 8 3 初始时,left = 0; right = 7; 将第一个数设为基数 base = a[left];
由于将a[0]保存到base中,可以理解为在a[0]处挖了一个坑,可以将数据填入a[0]中。
从最右边right挨个开始找比base小的数。当right==7符合,则将a[7]挖出来填入a[0]的坑里面(a[0] = a[7]),所以又 形成了新坑a[7],并且left ++。
再从左边left开始挨个找比base大的数(注意上一步left++),当left == 2符合,就将a[2]挖出来填入a[7]位置处,并且right–。
现在数组变为:
数组下标: 0 1 2 3 4 5 6 7
无序数列: 3 2 5 7 1 6 8 5 重复以上步骤,左边挖的坑在右边找,右边找到比基数小的填到左边,左边++。右边的坑在左边找,找到比基数大的填在右边,右边–。
循环条件是left > right,当排序完后,将基数放在循环停止的位置,比基数小的都到了基数的左边,比基数大的都到了基数的右边。
数组下标: 0 1 2 3 4 5 6 7
无序数列: 3 2 1 4 7 6 8 5 再对0~2区间和4~7区间重复以上操作。直到分的区间只剩一个数,证明排序已经完成。
可以看出快排是将数组一分为二到底,需要log N次,再乘以每个区间的排序次数 N。所以时间复杂度为:-O(N * log N)。
void Quicksort(int *array, int l, int r)
{
int i = 0;
int j = 0;
int x = 0;
if(l < r){
i = l;
j = r;
x = array[l];
while(i < j){
while(i < j && array[j] >= x){
j--;
}
if(i < j){
array[i++] = array[j];
}
while(i < j && array[i] <= x){
i++;
}
if(i < j){
array[j--] = array[i];
}
}
array[i] = x;
Quicksort(array, l, i - 1);
Quicksort(array, i + 1, r);
}
}快排还有许多改进版本,如随机选择基数,区间内数据较少时直接用其他排序来减小递归的深度等等。快排现在仍是很多人研究的课题,有兴趣的同学可以深入的研究下。
五,分而治之——归并排序
归并排序是建立在归并操作上的一种优秀的算法,也是采用分治思想的典型例子。
我们知道将两个有序数列进行合并,是很快的,时间复杂度只有-O(N)。而归并就是采用这种操作,首先将有序数列一分二,二分四……直到每个区都只有一个数据,可以看做有序序列。然后进行合并,每次合并都是有序序列在合并,所以效率比较高。
无序数组: 2 5 4 7 1 6 8 3
第一步拆分:2 5 4 7 | 1 6 8 3
第二步拆分:2 5 | 4 7 | 1 6 | 8 3
第三步拆分:2 | 5 | 4 | 7 | 1 | 6 | 8 | 3
第一步合并:2 5 | 4 7 | 1 6 | 3 8
第二步合并:2 4 5 7 | 1 3 6 8
第三步合并:1 2 3 4 5 6 7 可见归并排序的时间复杂度是拆分的步数 log N 乘以排序步数 N ,为-O(N * log N)。也是高级别的排序算法(-O(N ^ 2)为低级别)。
void Mergesort(int *array, int n)
{
int *temp = NULL;
if(array == NULL || n < 2)
return;
temp = (int *)Malloc(sizeof(int )*n);
mergesort(array, 0, n - 1, temp);
free(temp);
}
void mergesort(int *array, int first, int last, int *temp)
{
int mid = -1;
if(first < last){
mid = first + ((last - first) >> 1);
mergesort(array, first, mid, temp);
mergesort(array, mid+1, last, temp);
mergearray(array, first, mid, last, temp);
}
}
void mergearray(int *array, int first, int mid, int last, int *temp)
{
int i = first;
int m = mid;
int j = mid + 1;
int n = last;
int k = 0;
while(i <= m && j <= n){
if(array[i] <= array[j]){
temp[k++] = array[i++];
}else{
temp[k++] = array[j++];
}
}
while(i <= m){
temp[k++] = array[i++];
}
while(j <= n){
temp[k++] = array[j++];
}
memcpy(array + first, temp, sizeof(int) * k);
}由于要申请等同于原数组大小的临时数组,归并算法快速排序的同时也牺牲了N大小的空间。这是速率与空间不可调和矛盾,接触数据结构越多,越能发现这个道理,我们只能取速度与空间权衡点,不可能两者兼得。
六,缩小增量——希尔排序
希尔排序的实质就是分组插入排序,该方法又称为缩小增量排序,因DJ.Shell与1959年提出而得名。
该方法的基本思想是:先将整个待排序列分割成若干个子序列(由相隔某个”增量”的元素组成)分别进行插入排序,然后依次缩减增量再次进行排序,待整个序列中的元素基本有序时(增量足够小),再对全体进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的。
无序数组: 2 5 4 7 1 6 8 3
第一次gap=8/2 2A 1A
5B 6B
4C 8C
7D 3D设第一次增量为N/2 = 4,即a[0]和a[4]插入排序,a[1]和a[5]插入排序,a[2]和a[6],a[3]和a[7].字母相同代表在同一组进行排序。
排序完后变为:
一次增量: 1 5 4 3 2 6 8 7
A B C D A B C D 缩小增量,gap=4/2。
一次增量: 1 5 4 3 2 6 8 7
第二次gap=4/2 :1A 4A 2A 8A
5B 3B 6B 7B第二次增量变为2,即a[0],a[2],a[4],a[6]一组进行插入排序。a[1],a[3],a[5],a[7]一组进行排序。结果为:
二次增量: 1 3 2 5 4 6 8 7第三次增量gap=1,直接进行选择排序。
三次增量: 1 2 3 4 5 6 7 8希尔排序的时间复杂度为-O(N * log N),前提是使用最佳版本,后面有提到。
void Shellsort(int *array, int n)
{
int i,j,k,temp,gap;
for(gap = n/2; gap > 0; gap /= 2){
for(i = 0; i < gap; i++){
for(j = i + gap; j < n; j += gap){
for(k = j - gap; k >= i && array[k] > array[k+1]; k -= gap){
temp = array[k+1];
array[k+1] = array[k];
array[k] = temp;
}
}
}
}
} 很显然,上面的Shell排序虽然对直观理解希尔排序有帮助,但代码过长循环过多,不够简洁清晰。因此进行一下改进和优化,在gap内部进行排序显然也能达到缩小增量排序的目的。
void Shellsort(int *array, int n)
{
int i,j,k,temp;
for(gap = n/2; gap > 0; gap /= 2){
for(j = gap; j < n; j ++){
if(array[j] < array[j-gap]){
temp = array[j];
k = j - gap;
while(k >= 0 && array[k] > temp){
array[k+gap] = array[k];
k -= gap;
}
array[k+gap] = temp;
}
}
}
}希尔排序的缩小增量思想很重要,学习数据结构主要就是学习思想。我们上面排序的步长gap都是N/2开始,在进行减半,实际上还有更高效的步长选择,如果你有兴趣,可以去维基百科查看更多的步长算法推导。
七,集中数据的排序——计数排序
如果有这样的数列,其中元素种类并不多,只是元素个数多,请选择->计数排序。
比如一亿个1~100的整型数据,它出现的数据只有100种可能。这个时候计数排序非常的快(亲测,快排需要19秒,基数排序只需要不到1秒!)。
计数排序的思想是这样的:
1. 根据数据范围size(100),malloc构造一个用于计算数据出现次数的数组,并将其初始化个数都置为0。
2. 遍历一遍,将出现的每个数据的次数记录于数组。
3. 再次遍历,按照顺序并根据数据出现的次数重现摆放,排序完成。
可见计数排序仅仅遍历了两遍。时间复杂度:-O(N) + -O(N) = -O(N)。
void count_sort(int *array, int length, int min, int max)
{
int *count = NULL;
int c_size = max - min + 1;
int i = 0;
int j = 0;
count = (int *)Malloc(sizeof(int) * c_size);
bzero(count, sizeof(int) * c_size);
for(i = 0; i < length; ++i){
count[array[i] - min]++;
}
for(i = 0, j = 0; i < c_size;){
if(count[i]){
array[j++] = i + min;
count[i]--;
}else{
i++;
}
}
free(count);
}计数排序虽然时间复杂度最小,速度最快。但是,限制条件是数据一定要比较集中,要是数据范围很大,程序可能会卡死。
八,构造树——二叉堆排序
堆排序与快速排序,归并排序一样都是时间复杂度为 O(N*logN)的几种常见排序方法。学习堆排序前,先讲解下什么是数据结构中的二叉堆。
二叉堆的定义:
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:

由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储:
一般都用数组来表示堆,i 结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为 2 * i + 1 和 2 * i + 2。如第 0 个结点左右子结点下标分别为 1 和 2。
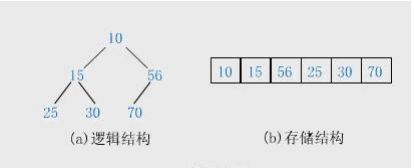
堆的操作——插入删除:
下面先给出《数据结构 C++语言描述》中最小堆的建立插入删除的图解,再给出代码实现,最好是先看明白图后再去看代码。

堆的插入:
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中,写出插入一个新数据时堆的调整代码:
void MinHeapFixup(int a[], int i)
{
int j,temp;
temp = a[i];
j = (i - 1) / 2; //父结点
while (j >= 0){
if (a[j] <= temp)
break;
a[i] = a[j]; //把较大的子结点往下移动,替换它的子结点
i = j;
j = (i - 1) / 2;
}
a[i] = temp;
}更简短的表达为:
void MinHeapFixup(int a[], int i)
{
for (int j = (i - 1) / 2; j >= 0 && a[i] > a[j]; i = j, j = (i - 1) / 2)
Swap(a[i], a[j]);
}插入时://在最小堆中加入新的数据nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
a[n] = nNum;
MinHeapFixup(a, n);
}堆的删除:
按定义,堆中每次都只能删除第 0 个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码:
// 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n){
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}堆化数组:
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
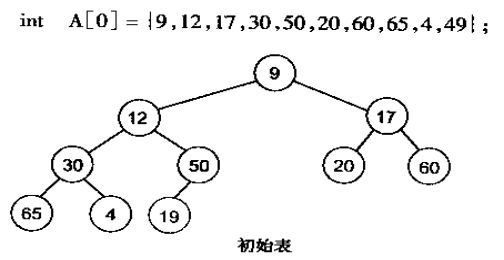
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即 20,60, 65,4, 49 都分别是一个合法的堆。只要从 A[4]=50 开始向下调整就可以了。然后再取 A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9 分别作一次向下调整操作就可以了。下图展示了这些步骤:

写出堆化数组的代码:
//建立最小堆
void MakeMinHeap(int a[], int n)
{
for (int i = n / 2 - 1; i >= 0; i--)
MinHeapFixdown(a, i, n);
}至此,堆的操作就全部完成了,再来看下如何用堆这种数据结构来进行排序。
堆排序:
首先可以看到堆建好之后堆中第 0 个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。
这样堆中第 0 个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。由于堆也是用数组模拟的,故堆化数组后,第一次将 A[0]与 A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将 A[0]与 A[n – 2]交换,再对 A[0…n - 3]重新恢复堆,重复这样的操作直到 A[0]与 A[1]交换。
由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
// 堆排序 最小堆 –> 降序排序
void MinheapsortTodescendarray(int a[], int n)
{
for (int i = n - 1; i >= 1; i--){
Swap(a[i], a[0]);
MinHeapFixdown(a, 0, i);
}
}注意使用最小堆排序后是递减数组,要得到递增数组,可以使用最大堆。由于每次重新恢复堆的时间复杂度为 O(logN),共 N - 1 次重新恢复堆操作,再加上前面建立堆时 N / 2 次向下调整,每次调整时间复杂度也为 O(logN)。二次操作时间相加还是 O(N * logN)。故堆排序的时间复杂度为 O(N * logN)。
八种排序算法已经介绍完毕,希望大家有所收获!
染尘 16.4.29