线性回归与正则化
线性回归与正则化
线性回归总述
追根溯源,回归(Regression)这一概念最早由英国生物统计学家高尔顿和他的学生皮尔逊在研究父母亲和子女的身高遗传特性时提出。他们的研究揭示了关于身高的一个有趣的遗传特性:若父母个子高,其子代身高高于平均值的概率很大,但一般不会比父母更高。即身高到一定程度后会往平均身高方向发生“回归”。这种效应被称为“趋中回归(Regression Toward the Mean)”。如今,我们做回归分析时所讨论的“回归”和这种趋中效应已经没有任何瓜葛了,它只是指源于高尔顿工作的那样一整套建立变量间数量关系模型的方法和程序,即用一个或多个自变量来预测因变量的数学方法。
回归分析之所以成为一种重要的统计模型,是因为它关注的是现象解释和预测,而不仅是描述层面的统计分析。在一个回归模型中,我们需要关注或预测的变量叫做因变量(响应变量或结果变量),我们选取的用来解释因变量变化的变量叫做自变量(解释变量或预测变量)。做回归分析,确定变量后我们还需要根据具体问题选择一个合适的回归模型,通俗地说就是把自变量映到因变量的函数的大体样子。常用的回归模型有线性回归,多项式回归,逻辑斯蒂回归等等。考虑到线性关系是自然界最普遍,最本质的数量关系,所以毋庸置疑线性回归是最简单实用的一类回归模型,也是其他回归模型研究的基础。本节我们主要讨论线性回归的相关理论及部分应用场景。
一元线性回归
让我们从最简单的一元线性回归说起。现有自变量 X ,因变量 Y ,模型为
其中 k,b 是模型参数, ε 为残差。面对一个具体问题,我们拿到样本点,即 X,Y 的观测值是 (x1,y1),...,(xn,yn) ,我们的目标是找到一条直线 y=kx+b 使得所有样本点尽可能落在它的附近。换句话说就是让 ε 在某种意义上极小化残差 ε .在高中我们就熟知这个问题的解法——求解使得 εi(i=1,2,...,n) 的平方和极小化的 k,b ,即
以上关于 (k,b) 的无约束二次优化问题,其解析解是容易得到的。这个方法叫做最小二乘法(Ordinary Least Square, OLS)。直观上,这个算法给出了描述 X,Y 两个变量线性关系的最优近似。
多元线性回归
多元线性回归本质也是一样,只是自变量和参数的个数变为 k 个。我们的目的仍是在最小二乘的意义下找到让残差平方和极小的参数。模型为
其中 Y=(y1,...,yn)T 为因变量,有 n 个观测值; X=(xij)n×k 为 n×k 矩阵,其 k 个列分别表示 k 个自变量的 k×n 个观测值; β=(β1,...,βk) 为自变量的回归系数, ε 为残差。若考虑截距项,可在 X 中加入一列常数,出于简单起见暂不考虑。
这个问题在OLS意义下的解为
上式称作法方程。
最小二乘法的合理性
1829年高斯提出最小二乘法,然而实际上早在1760年波斯科维奇就提出了最小一乘法。最小一乘在数学上更简单也更符合人们的直觉,但为什么实际中却很少有人使用?最小二乘究竟有什么优势?为什么回归模型的训练准则是最小化残差的平方和,不是绝对值的总和,立方和,四次方和或是别的什么?要回答这些问题,我们必须深入理解OLS条件的本质。
线性代数给出的理由
从线性代数的角度来看,多元回归是一个典型的最佳逼近问题。即在 X 的列向量所张成的 k 维线性空间 Vk 中找一个元素 Yk=Xβ ,使得 Yk∈Vk 与 Y∈Vn 在某种度量的意义下距离最短。于是自然地,我们选取欧氏距离作为度量,这就是OLS中残差平方和的由来。
具体来讲,选取欧氏距离带来的好处在于使得线性空间 Vn 及其子空间 Vk 成为内积空间,从而具备了良好的几何性质。在欧氏度量的意义下, Y 在 Vk 中的最佳逼近元 Yk 正是 Y 在 Vk 上的正交投影,于是我们有
即 ε⊥X,XTε=0 .这样一来,在回归方程的两边同时左乘 (XTX)−1XT 立刻解得 β∗=(XTX)−1XTY .这就是著名的法方程(Normal Equation)。
数理统计给出的理由
从数理统计的角度来看,多元回归是一个典型的参数估计问题。OLS的好处在于,在一定条件条件下它得到的估计拥有统计上的优良性质。严格来说,要对模型提以下条件:
1、误差 ε 是一个期望0的随机向量;
2、对于解释变量的所有观测值, ε 的各个分量有相同的方差,且彼此不相关;
3、解释变量与随机误差项彼此相互独立;
4、解释变量之间不存在精确的线性关系;
5、随机误差项服从正态分布。
在条件1,2,3,4成立的前提下,我们有著名的高斯-马尔科夫定理(Gauss-Markov Thm.):最小二乘估计是最小方差线性无偏估计,即“OLS is BLUE(Best Linear Unbiased Estimator)”.在5个条件全部成立的前提下,还不难证明最小二乘估计是极大似然估计。
理论上第5个条件并不是硬性的,但实际问题中我们一般希望它能够满足。毕竟,若只要模型足够好以至于选取的自变量确实与因变量线性相关,那么残差与预测值就应该没有任何系统关联,于是当数据量足够大时它理应服从正态分布*(关于这一点的深入讨论读者可以自学广义线性模型(Generalized Linear Model,GLM),GLM关注的就是当给定自变量后因变量服从某指数分布族分布的一般情形)。此外,残差满足正态分布的假设还有助于我们在做回归结果诊断时对模型参数进行显著性检验。
回归结果诊断
在数据基本满足模型假设的前提下,我们容易通过求解法方程得到模型参数。然而此时我们需要一些指标来帮助判断我们最终得到的模型是否合适,这就需要进行结果诊断。
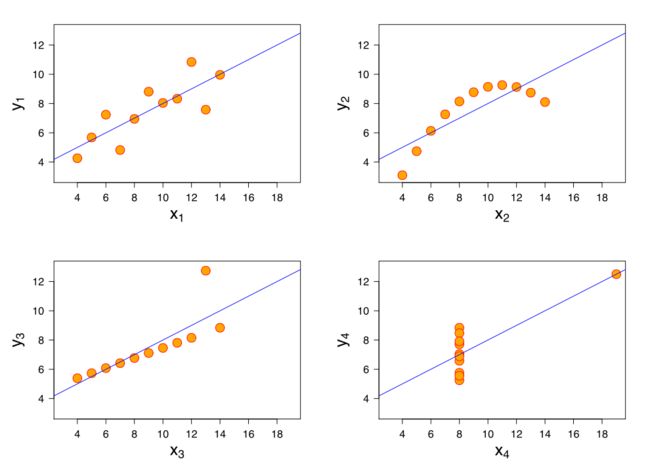
为了说明结果诊断的重要性,我们先来看一个著名例子(Anscombe’s quartet,图来自维基百科)
对这四组观测数据,我们用线性回归将得到完全相同的模型,但它们的解释力显然大相径庭。这个例子告诉我们,在接受一个回归结果之前需要检验的事项至少有如下几条:
1. 残差是否近似满足均值为0的正态分布,这一点可以通过观察残差分布QQ图来验证;
2. 因变量值是否独立,这一点要从搜集的数据出发直接验证;
3. 是否存在离群点,高杠杆值点或强影响点;
接受一个回归模型之后,我们还需要设计一些指标去衡量它的效果。最重要的指标有如下几个:
1. R2 值,衡量模型拟合优度:
2. F值,衡量拟合方程的显著性
3. t值,衡量各个变量拟合系数的显著性
这些功能都包含在R的线性回归工具包中。
岭回归与LASSO
变量选择是多元线性回归不可回避的重要问题,这一步骤的好坏直接影响到模型效果。线性回归作为一种统计学习算法,也会出现过拟合的问题。若只是尽可能地去拟合样本数据,回归模型的参数个数会过多(选取过多的自变量),或者拟合出来的参数绝对值很大(自变量间存在多重共线性),这样不仅会导致差强人意的泛化能力,还大大降低了模型的可解释性(对统计学家来说,可解释性非常重要。eg医生研究疾病的例子)。为避免出现过拟合,我们可以使用带正则化的线性回归模型。
所谓正则化,就是对模型的参数添加一些先验假设,控制模型空间,以达到使得模型复杂度较小的目的。岭回归(Ridge Regression)和LASSO(Least Absolute Shrinkage and Selection Operator)是目前最为流行的两种线性回归正则化方法。具体来讲,岭回归和LASSO分别对应 L2 , L1 正则化( L0 正则化带来NP难的组合优化问题),对 β 提的先验假设分别为 ||β||2≤C 和 ||β||1≤C , C 为预先取定的常数。也就是说,关注下面带约束的优化问题
以及
利用拉格朗日乘子法,易知以上约束优化问题等价于无约束的罚函数优化问题
以及
其中 λ 为依赖于 C 的常数。
对岭回归,直接求导易得
和法方程比较,可以看到岭回归得到的估计只多了一个正则项 λI .这一项的存在使得 (XTX+λI)−1 在数值计算上表现更加稳定。尤其是当多重共线性(Multicollinearity)情况发生, XTX 接近奇异时,岭回归还是能得到稳定的结果。另外,在岭回归中还可以通过观察岭迹来剔除多重共线性的变量。
LASSO的解 βLASSO 没有解析表达式,但比起岭回归却有其独到的优势—— βLASSO 是稀疏的,即很多分量恰好为0.这一优良的性质是由一范数在坐标轴上一阶不可导所决定的。因此,LASSO模型得到的结果可以帮助我们做特征选择。当某个 Xi 和Y相关性不高或者和其他 Xj 存在多重共线性情况时, βLASSOi 极有可能等于0.
正则化的本质,其实是在估计参数 β 时做一个bias 和 variance 的trade-off.高斯马尔科夫定理告诉我们,不带正则化的线性回归模型得到的参数 β 已经是最小方差无偏估计。换句话说,若不放弃无偏性是没有办法改进模型效果的。岭回归和LASSO作为有偏估计,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价,以期望获得更为符合实际的回归系数。他们对病态数据的耐受性远远强于最小二乘法。
线性回归R实战
最后总结一下建立回归模型的基本步骤:
| 模型建立的基本步骤 | 回归模型 |
|---|---|
| 特征选择 | 选取因变量 |
| 模型选择 | 选取回归函数 |
| 参数训练 | 定义回归残差 |
| 效果检验 | 回归诊断 |
分析实际问题时,我们自己去实现其中的每一个细节,因为开源软件R已经为我们提供了丰富而完善的线性回归工具包。
在R中,线性回归的基本函数是lm().例如,我们选取的自变量为 X1,X2,X3 ,因变量为 Y ,数据为dataFrame,则调用的格式为
myLinearModel = lm(Y ~ X_1 + X_2 + X_3, data = dataFrame);
其中第一个参数为回归函数的表达式formula,第二个参数为回归数据data.formula可以灵活选取,甚至不仅局限于线性模型:
| 表达式 | 回归函数 |
|---|---|
| Y ~ | 包含data中除Y之外所有变量的线性项 |
| Y ~ X_1 + X_2 + X_3 | y ~ x1+x2+x3+b |
| Y ~ X_1 + X_2 + X_3 - 1 | y ~ x1+x2+x3 |
| Y ~ X_1 + I(X_2 ^ 2) | y ~ x1+x22 |
| Y ~ X_1 + X_2 : X_3 | y ~ x1+x2×x3 |
| Y ~ X_1 * X_2 * X_3 | y ~ x1+x2+x3+x1×x2+x2×x3+x3×x1+x1×x2×x3 |
对lm()得到的对象myLinearModel,将回归分析的相关函数作用于它可以得到我们关心的模型信息。常用的分析函数有
| 函数 | 用途 |
|---|---|
| summary() | 显示模型详细信息 |
| fitted() | 列出拟合模型的预测值 |
| confint() | 列出模型参数的置信区间 |
| plot() | 生成回归诊断图 |
| predict() | 对新的数据预测因变量值 |
另外R语言中岭回归的包是library(MASS), 通过函数是lm.ridge()进行调用。
R语言中LASSO的包是library(lars), 通过lars()进行调用。