静态数组表示的有限状态机

2013-07-13 16:18  745人阅读  评论(1)  收藏  举报

前段时间搞无状态的TCP conntrack，发现其中一个静态数组表示的TCP状态机很是不错，希望这种思想以后可以用在实际的工作中，直说吧，就是这个状态机数组：

 static const u8 tcp_conntracks[2][6][TCP_CONNTRACK_MAX] = {
     {
 /* ORIGINAL */
 /*          sNO, sSS, sSR, sES, sFW, sCW, sLA, sTW, sCL, sS2    */
 /*syn*/       { sSS, sSS, sIG, sIG, sIG, sIG, sIG, sSS, sSS, sS2 },
 /*
 ...
 };

以下是状态机转换公式：
new_state = tcp_conntracks[dir][index][old_state];
上述公式中，dir就是IP_CT_DIR_REPLY或者IP_CT_DIR_ORIGINAL，index其实就是事件。初看，就可以看出这个要比一个while循环实现的状态机，原因就在于状态机完全数据化了，而不是常规的那样用代码逻辑if state-if event或者switch-case等硬编码完成的。在这个数组填充的时候，那些if state-if event等判断就已经做好了，数组填充完成了，直接拿来用就是了。
        实际上，在Linux内核中，这样的实现还不止conntrack一个，IPVS也是一个很好的例子，net/netfilter/ipvs/ip_vs_proto_tcp.c：

 static struct tcp_states_t tcp_states [] = {
 /*    INPUT */
 /*        sNO, sES, sSS, sSR, sFW, sTW, sCL, sCW, sLA, sLI, sSA    */
 /*syn*/ {{sSR, sES, sES, sSR, sSR, sSR, sSR, sSR, sSR, sSR, sSR }},
 /*fin*/ {{sCL, sCW, sSS, sTW, sTW, sTW, sCL, sCW, sLA, sLI, sTW }},
 /*ack*/ {{sCL, sES, sSS, sES, sFW, sTW, sCL, sCW, sCL, sLI, sES }},
 /*rst*/ {{sCL, sCL, sCL, sSR, sCL, sCL, sCL, sCL, sLA, sLI, sSR }},
 ...
 };

可见和ip_conntrack的极其类似！这种数组所包含的信息量极大，几乎把索引下标，数组维数全部都用来存储数据了，这样就形成了一个多维的存储结构，一旦两个维度的信息不再正交，那么数组元素本身它就有了状态，而这正是实现状态机的关键。

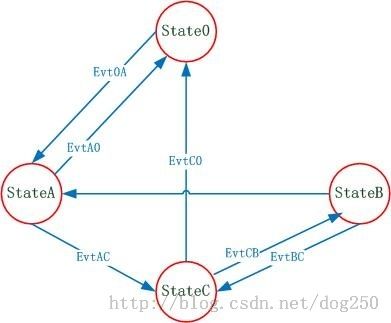
        我这里给出一个例子，下图是一个一般的状态机

以下就需要用该状态机构造一个数组，填充每一个元素，最终把这个静态数组写入.h文件中，若计算机自己有智能，那么这个填充工作完全可以在运行时完成，然而计算机没有智能，所以只能程序员写好它。如果非要运行时填充，那么填充代码本身的代码还是回归到了while循环处理状态机了。
        填充过程很简单，公式如下：
StateMachine[Event][OldSate]=NewState;
为此，我们先定义一套数据，将State和Event数据化：

 /*状态定义*/
 enum State{
     State0=0,
     StateA=1,
     StateB=2,
     StateC=3,
 };
 /*事件定义*/
 enum Event{
     Einit=0,
     Evt0A=1,
     EvtA0=2,
     EvtAC=3,
     EvtC0=4,
     EvtCB=5,
     EvtBC=6,
 };

我们定义一个二维数组，第一维代表事件，第二维的值代表下一个状态第二维的索引，其实就是下面的公式
NewState=StateMachine[Event][OldState];
按照上面的填充规则，终于，我们得到了下面的这个数组：

 StateMachine[][]=
 {
 /*Einit*/       {State0,}
 /*Evt0A*/    {StateA,},
 /*EvtA0*/    {stub,State0,},
 /*EvtAC*/    {stub,StateC,},
 /*EvtC0*/    {stub,stub,stub,State0,},
 /*EvtCB*/    {stub,stub,StateB,},
 /*EvtBC*/    {stub,stub,StateC,},
 }

其中的stub表示该处不表示任何状态。

       看懂了这个例子以后，再回过头上ip_conntrack以及ipvs的TCP的状态机数组的例子，就更加清晰了，唯一不同的是，ip_conntrack通过一个新的维度来表示数据方向，而ipvs则通过一个base+offset的方式定位到了事件维度数组的索引。最后把上面的过程做成了一张图：

总结：

我们知道，任何程序都可以表示成一个状态机，这也是程序的本质，它本质上就是下面的形式：
if (match0) {
    do_something0;
} elif (match1) {
    do_something1;
} elif (match2) {
    do_something2;
}
但凡可以用这种方式表示的逻辑，都可以用一个多维数组来表示。常见的如BPF或者其它的过滤机制，本质上也是一些叠加判断：
if (match0 && match1 && match2 && match 3 && ...) {
   return TRUE;
} else {
   return FALSE;
}
把每一个match作为数组的一个维度，就可以构造出一个数组，最终是否匹配的判断就转换成根据诸多match计算出的数组各维度索引指示的目标位置的元素是否为NULL(或者上述简单例子的stub)。可是且慢！上述的思路有一个大前提，那就是填充数组的那个人或者那个程序必须事先知道结果才行，对于既有的有限状态机，这是肯定的，然而对于上述的多match元素匹配，填充者在拿到输入前并不知道结果(有点废话，要是知道了结果还要那个判断程序干什么！！)，因此必须让输入也参与到数组中来才行，因此必然这个输入是有限个的，毕竟数组必须是有限维度的。

更多 0

• 上一篇无状态TCP的ip_conntr