从导数的物理意义理解梯度下降

机器学习中常会用随机梯度下降法求解一个目标函数 L(Θ) ，并且常是最小化的一个优化问题：

min L(Θ)

我们所追求的是目标函数能够快速收敛或到达一个极小值点。而随机梯度法操作起来也很简单，不过是求偏导数而已，但是为什么是这样呢？为什么算出偏导数就能说下降得最快？初期并不很明了，后来看过一些数学相关的知识才稍微明白了一点，以下内容算是一个理解梯度的渐进过程。如果不当之处，欢迎指正。

以下关于梯度下降法，导数，偏导数的内容可在维基百科中找到，关于方向导数与梯度的内容可在高等数学书中找到。

预备知识

既然是从导数的物理意义进行理解，必然要先了解其物理意义是什么。 在以下内容中， 导数与偏导数大多数人都很熟悉， 请重点关注方向导数与梯度。

梯度下降法简介

梯度下降法（Gradient descent）是一个最优化算法，通常也称为最速下降法（Deepest gradient）。

梯度下降法，基于这样的观察：如果实值函数 F(x) 在点 a 处可微且有定义，那么函数 F(x) 在 a 点沿着梯度相反的方向 −∇F(a) 下降最快。

因而，如果 b=a−γ∇F(a)
对于 γ>0 为一个够小数值时成立，那么 F(a)≥F(b) 。

考虑到这一点，我们可以从函数F的局部极小值的初始估计 x0 出发，并考虑如下序列

x0 , x1 , x2 , …

使得 xn+1=xn−γn∇F(xn) ,  n≥0 。

因此可得到
F(x0)≥F(x1)≥F(x2)≥⋯ ,

如果顺利的话序列 (xn) 收敛到期望的极值。注意每次迭代步长 γ 可以改变。

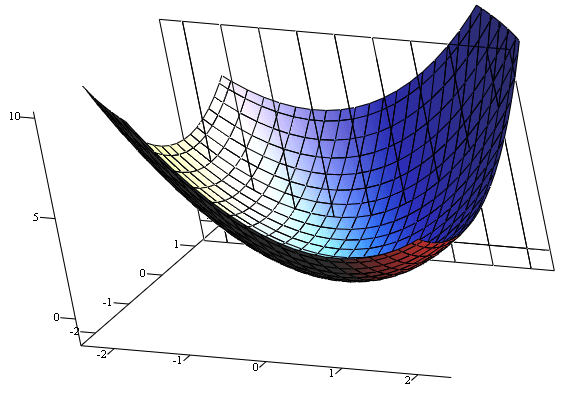
下面的图片示例了这一过程，这里假设F定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数F为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数F值最小的点。

求解机器学习中的 min L(Θ) 问题，可以选择采用梯度下降法。

梯度下降法的缺点如下，为何可能会有下面的缺点，可在梯度下降法的维基百科中看到更多内容。这里仅当一个搬运工而已：

• 靠近极小值时速度减慢。

• 直线搜索可能会产生一些问题。

• 可能会’之字型’地下降。

导数

导数（Derivative）是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

当函数 f 的自变量在一点 x0 上产生一个增量 h 时，
函数输出值的增量与自变量增量 h 的比值在 h 趋于 0 时的极限如果存在，即为 f 在 x0 处的导数，记作 f′(x0) 、 dfdx(x0) 或 dfdx∣∣x=x0 .

物理意义上， 导数表示函数值在这一点的变化率。

偏导数

在数学中，一个多变量的函数的偏导数是它关于其中一个变量的导数，而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。

假设 ƒ 是一个多元函数。例如：

f(x,y)=x2+xy+y2

f=x2+xy+y2 的图像。我们希望求出函数在点（1, 1, 3）的对 x 的偏导数；对应的切线与xOz平面平行。

因为曲面上的每一点都有无穷多条切线，描述这种函数的导数相当困难。偏导数就是选择其中一条切线，并求出它的斜率。通常，最感兴趣的是垂直于y轴（平行于xOz平面）的切线，以及垂直于x轴（平行于yOz平面）的切线。

一种求出这些切线的好办法是把其他变量视为常数。例如，欲求出以上的函数在点（1, 1, 3）的与xOz平面平行的切线。上图中显示了函数 f=x2+xy+y2 的图像以及这个平面。下图中显示了函数在平面y = 1上是什么样的。我们把变量y视为常数，通过对方程求导，我们发现 ƒ 在点（x, y, z）的。我们把它记为：
∂z∂x=2x+y ，于是在点（1, 1, 3）的与xOz平面平行的切线的斜率是3。 ∂f∂x=3 在点（1, 1, 3），或称“f在（1, 1, 3）的关于x的偏导数是3”。

在几何意义上偏导数即为函数在坐标轴方向上的变化率。

方向导数

方向导数是分析学特别是多元微积分中的概念。一个标量场在某点沿着某个向量方向上的方向导数，描绘了该点附近标量场沿着该向量方向变动时的瞬时变化率。方向导数是偏导数的概念的推广。

方向导数定义式：

方向导数计算公式（在推导方向导数与梯度关系时用到）：

几何意义上方向导数为函数在某点沿着其他特定方向(也便是这里的 l 方向）上的变化率。

梯度

在一个数量场中，函数在给定点处沿不同的方向，其方向导数一般是不相同的。那么沿着哪一个方向其方向导数最大，其最大值为多少? 这是我们所关心的问题， 为此引进一个很重要的概念 –> 梯度。假设在点 p0 处， 函数值沿哪一方向增加的速度最快？ 先说结论，沿着梯度方向增加的速度最快。

为什么沿着梯度方向，函数值增加最快

这里可以从方向导数与梯度的关系进行推导：

总结

函数在某一点处的方向导数在其梯度方向上达到最大值，此最大值即梯度的范数。

这就是说，沿梯度方向，函数值增加最快。同样可知，方向导数的最小值在梯度的相反方向取得，此最小值为最大值的相反数，从而沿梯度相反方向函数值的减少最快。详细内容：方向导数与梯度。

在机器学习中往往是最小化一个目标函数, 最大化问题也可转换为最小化问题， min L(Θ) ，理解了上面的内容，便很容易理解在梯度下降中常用的更新公式：

θ=θ−γ∂L∂θ

γ 在机器学习中常被称为学习率 ( learning rate ) , 也就是上面梯度下降法中的步长。

通过算出目标函数的梯度并在其反方向更新完参数 θ ，在此过程完成后也便是达到了函数值减少最快的效果，那么经过迭代以后目标函数即可很快地到达一个极小值。

注：
本文如有后续更新内容可在我的github博客找到，欢迎访问。