【Algorithm】棋盘覆盖问题
这是我CSDN博客上第100篇原创博文,之前是计划写一篇关于Android源码分析的博文,但是Android源码还在阅读中,目前还没有较好的体会要分享。今天在做一道算法题,许久没写,有点生疏了。
题目描述如下:
在一个2^k×2^k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。显然,特殊方格在棋盘中可能出现的位置有4^k种,因而有4^k种不同的棋盘,图(a)所示是k=2时16种棋盘中的一个。棋盘覆盖问题(chess cover problem)要求用图(b)所示的4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
我尝试了两种实现方法。第一种是暴力地遍历,很显然,这中方法效率是极低的同时也是比较麻烦的。遍历的策略比较重要,不能重复也不能遗漏。我写完后测试,图稍微大一点就直接爆栈,还不仅仅是效率低的问题。递归的层次深,明显吃不消。
然后我尝试了第二种方法,分治&递归。这也是大部分人的解法,效率自然是数量级的提升。
大体分析如下:
1.分治首先自然是要进行划分。 我将棋盘横竖对切分为四块。这样就分出一块有一个特殊方格的和三个没有特殊方格的
2.进行依次划分后,接下来是递归。递归的前提是子问题规模较父问题小但是形式上得一样。从第一步可以知道:
有一块是有一个特殊方格的。这个特殊的方格明显是不能“吃掉”的。所以我将另外三个方格也给添加一个特殊方 格。
例如:
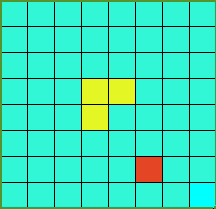
本来初始棋盘是这样的(红色为特殊方块):
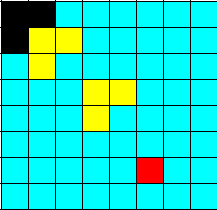
然后我进行划分后给其他三块没有特殊方块的添加上“特殊方块”。因为题目中要求,要用“L”形骨牌进行覆盖,因此
我只能在它们的连接处添加。
添加后如下:
这就进行了第一次划分。
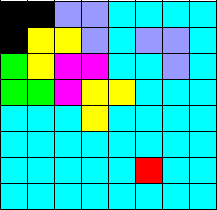
接下来就按照同样的方法对划分后的字块继续划分。
就画这么多了.....
这样代码实现也就简单了
直接上代码:
/*
Author:MummyDing
Date:18/10/2015
Algorithm:ChessBoard Coverage
*/
#include<iostream>
#include<stdio.h>
#define N 500
using namespace std;
int chess[N][N]={0};
int n;
int dir[4][3][2]={
{{0,1},{1,0},{1,1}},{{0,-1},{1,-1},{1,0}},
{{-1,0},{-1,1},{0,1}},{{-1,-1},{-1,0},{0,-1}}
};
void print(){
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
printf(j== n-1 ? "%d\n":"%d ",chess[i][j]);
}
int calcType(int sx,int sy,int halfX,int halfY){
int type = 0;
if(sx > halfX) type+=2;
if(sy > halfY) type++;
return type;
}
void getXY(int &px,int &py,int type){
if(type == 1) py++;
else if(type==2)px++;
else if(type==3)px++,py++;
}
void fillBoard(int x,int y,int sx,int sy,int width){
if(width == 1) return;
int midX = width/2 + x -1;
int midY = width/2 + y -1;
int type = calcType(sx,sy,midX,midY);
int px = midX, py = midY;
getXY(px,py,type);
for(int i=0;i<3;i++){
int tmpX = px+dir[type][i][0];
int tmpY = py+dir[type][i][1];
chess[tmpX][tmpY] = type+1;
}
if(width == 2) return;
for(int i =0 ;i<4;i++){
if(i==0){
if(i==type) fillBoard(x,y,sx,sy,width/2);
else fillBoard(x,y,midX,midY,width/2);
}else if(i==1){
if(i==type) fillBoard(x,width/2+y,sx,sy,width/2);
else fillBoard(x,width/2+y,midX,midY+1,width/2);
}else if(i==2){
if(i==type) fillBoard(width/2+x,y,sx,sy,width/2);
else fillBoard(width/2+x,y,midX+1,midY,width/2);
}else{
if(i==type) fillBoard(width/2+x,width/2+y,sx,sy,width/2);
else fillBoard(width/2+x,width/2+y,midX+1,midY+1,width/2);
}
}
}
int main(){
cout<<"Input the width"<<endl;
cin>>n;
cout<<"Input x and y:"<<endl;
int x,y;
cin>> x>>y;
x--,y--;
chess[x][y]=5;
fillBoard(0,0,x,y,n);
print();
return 0;
}
【转载请注明出处】
Author: MummyDing
出处:http://blog.csdn.net/mummyding/