USACO-Section 3.3 Camelot (最短路&&枚举)
此处有目录↑
描述
很久以前,亚瑟王和他的骑士习惯每年元旦去庆祝他们的友谊。为了纪念上述事件,我们把这些是看作是一个有一人玩的棋盘游戏。有一个国王和若干个骑士被放置在一个由许多方格组成的棋盘上,没有两个骑士在同一个方格内。
这个例子是标准的8*8棋盘
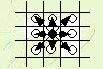
国王可以移动到任何一个相邻的方格,从下图中黑子位置到下图中白子位置前提是他不掉出棋盘之外。
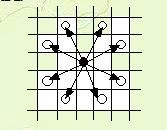
一个骑士可以从下图中黑子位置移动到下图中白子位置(走“日”字形) 但前提是他不掉出棋盘之外。
在游戏中,玩家可在每个方格上放不止一个棋子,假定方格足够大,任何棋子都不会阻碍到其他棋子正常行动。
玩家的任务就是把所有的棋子移动到同一个方格里——用最小的步数。为了完成这个任务,他必须按照上面所说的规则去移动棋子。另外,玩家可以选择一个骑士跟国王从他们两个相遇的那个点开始一起行动,这时他们按照骑士的行动规则行动,其他的单独骑士则自己一直走到集中点。骑士和国王一起走的时候,只算一个人走的步数。
写一个程序去计算他们集中在一起的最小步数,而且玩家必须自己找出这个集中点。当然,这些棋子可以在棋盘的任何地方集合。
[编辑]格式
PROGRAM NAME: camelot
INPUT FORMAT
(file camelot.in)
第一行: 两个用空格隔开的整数:R,C 分别为棋盘行和列的长。不超过26列,30行。
第二行..结尾: 输入文件包含了一些有空格隔开的字母/数字对,一行有一个或以上。第一对为国王的位置,接下来是骑士的位置。可能没有骑士,也可能整个棋盘都是骑士。行从1开始,列从大写字母A开始。
OUTPUT FORMAT
(file camelot.out)
单独一行表示棋子集中在一个方格的最小步数。
[编辑]SAMPLE INPUT
8 8 D 4 A 3 A 8 H 1 H 8
国王位置在D4。一共有四个骑士,位置分别是A3,A8,H1和H8。
[编辑]SAMPLE OUTPUT
10
他们集中在B5。
骑士1: A3 - B5 (1步)
骑士2: A8 - C7 - B5 (2步)
骑士3: H1 - G3 - F5 - D4 (此时国王开始与这个骑士一起走) - B5 (4步)
骑士4: H8 - F7 - D6 - B5 (3步)
1 + 2 + 4 + 3 = 10步
最开始没注意到有国王,就想到直接先用BFS处理出任意两点间的“最短路”,然后枚举终点即可,复杂度是O(n*m)
后来发现有国王,还是往枚举的方向想,可以枚举搭载国王的骑士,再枚举搭载国王的点,复杂度O((n*m)^3),估计很容易就超时,加了点剪枝,最慢的点0.85s,应该是服务器好,险过
官方是对每一点处理出两个值:①骑士到该点最短路,②骑士搭载王到该点的最短路,这样最慢的点0.4s
也有大神用dp过,不过看不懂...
/*
ID: your_id_here
PROG: camelot
LANG: C++
*/
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
struct Node {
int r,c;
Node(int rr=0,int cc=0):r(rr),c(cc) {}
}u,king,knight[30*26+5];
int dis[31][27][31][27],n,m,desR,desC,num;//dis[i][j][k][l]表示(i,j)和(k,l)两点见骑士走的最少步数
bool vis[31][27];
const int dr[8]={-2,-1,1,2,2,1,-1,-2};
const int dc[8]={1,2,2,1,-1,-2,-2,-1};
inline bool isInside(int r,int c) {
return 0<=r&&r<n&&0<=c&&c<m;
}
void bfs() {
int r,c,step;
queue<Node> q;
q.push(Node(desR,desC));
memset(vis,false,sizeof(vis));
dis[desR][desC][desR][desC]=0;
vis[desR][desC]=true;
while(!q.empty()) {
u=q.front();
q.pop();
step=dis[desR][desC][u.r][u.c];
for(int i=0;i<8;++i) {
r=u.r+dr[i];
c=u.c+dc[i];
if(isInside(r,c)&&!vis[r][c]) {
vis[r][c]=true;
dis[desR][desC][r][c]=step+1;
q.push(Node(r,c));
}
}
}
}
void solve() {
memset(dis,0x0f,sizeof(dis));//最大值不能初始化太大否则枚举的终点存在多个骑士均不能到达时,all会溢出(推荐用循环赋更小的值,即使0x01多了也可能会溢出)
for(desR=0;desR<n;++desR)//预处理任意两点间,骑士走的最少步数
for(desC=0;desC<m;++desC)
bfs();
int ans=0x3f3f3f3f,all,cur,kn,r,c,knr,knc;
for(desR=0;desR<n;++desR) {
for(desC=0;desC<m;++desC) {//枚举终点
all=0;
for(kn=0;kn<num;++kn)
all+=dis[desR][desC][knight[kn].r][knight[kn].c];
ans=min(ans,all+max(abs(king.r-desR),abs(king.c-desC)));//由于可能没有骑士,则一下循环无法执行,所以在此让国王自己走到终点
for(kn=0;kn<num;++kn) {//枚举搭载国王的骑士
knr=knight[kn].r;
knc=knight[kn].c;
cur=all-dis[desR][desC][knr][knc];
if(0<=cur&&cur<ans) {//剪枝
for(r=0;r<n;++r) {
for(c=0;c<m;++c) {//枚举搭载国王的点
ans=min(ans,cur+dis[r][c][knr][knc]+dis[desR][desC][r][c]+max(abs(king.r-r),abs(king.c-c)));
}
}
}
}
}
}
printf("%d\n",ans);
}
int main() {
freopen("camelot.in","r",stdin);
freopen("camelot.out","w",stdout);
num=0;
scanf("%d%d",&n,&m);
char pc[3];
int pr;
scanf("%s%d",pc,&pr);
king.r=pr-1;
king.c=pc[0]-'A';
while(2==scanf("%s%d",pc,&pr)) {
knight[num].r=pr-1;
knight[num++].c=pc[0]-'A';
}
solve();
return 0;
}