跳跃表(续)
http://blog.csdn.net/qq575787460/article/details/16371287上一篇引入了跳跃表的介绍,并且测试了跳跃表的插入和查找效率。可以看到在大量数据中效率明显高于红黑树。(当然带来的空间的巨大浪费)。
那么跳跃表为什么会快呢?下来看一个生活中的例子。
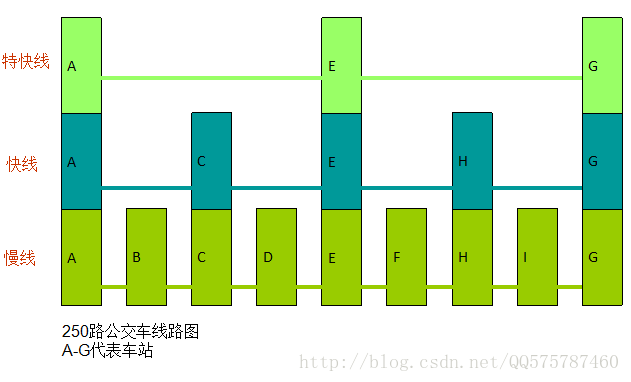
如图,A--G分别代表250路公交车经过的车站。有特快,快和慢3条线路。
特快的只在A,E,G站牌停车。
快线只在A,C,E,H,G站牌停车。
慢线则在所有的站牌停车。
如果我想A站坐到I站,那么最快的乘车方案就是
A站牌---特快线---E站牌---换成快线---H站牌---换成慢线---I站牌。
是不是很像跳跃表?
并且在上一篇博客中测试情况看来,跳跃表与红黑树的查找效率差别不大,而跳跃表的插入效率明显高于红黑树。究其原因,跳跃表在插入的时候,只需要记下来插入一个节点需要更新哪一层的哪个节点就行了,而红黑树则需要回溯的对整个插入路径调整。
在插入节点时,我们是随机的给新节点一个层次高度,其实并不是随机。
int get_rand_lvl()
{
int lvl = 1;
while ((rand() & 0xffff) < (0xffff >> 2))
lvl++;
return lvl;
}关键是要理解while循环中的那一句是什么意思?
rand() & 0xffff 意思是随机一个0---0xffff之间的整数。
0xffff >> 2 意思是0xffff的四分之一
可以把while循环理解为产生一个0--1之间的小数,如果这个小数小于0.25,那么把层数+1,并且进行下一次while循环。
是不是感觉很诡异,为什么不直接随机一个1---MAX_LVL之间的数呢?
我想了好几天,终于知道了,这涉及到了层次分布的问题。
通过while循环来产生层次,那么层次越大,几率越低。
例如,lvl=1的概率为0.75(第一次while就为false)
lvl=2的概率为0.25
lvl=3的概率为0.25*0.25
lvl=4的概率为0.25*0.25*0.25
所以,如果数据量非常大,那么整个跳跃表看起来是波浪线非常明显的。
而如果直接随机出来一个高度,那么高度的分布均匀了,反而不利于查找。
跳跃表的源码点击打开链接