Markov定位

一.Markov定位算法说明

        Markov定位初始化时让所有位姿的置信度服从均匀分布，然后从里程计获得当前时刻与上一时刻的差值作为测量值。

1.预测

        对上一时刻t-1在所有位姿处的概率根据下式更新当前时刻t在i处的概率，可以看成是以里程计测量值为基础得到xi处的概率，前提是已知上一时刻所有位姿到位姿i的状态转移概率和上一时刻所有位姿的概率。假设当前状态仅仅取决于上一时刻的状态和当前时刻的测量值。

   （*）例：

        假设机器人安装编码器和罗盘，位于下面16单元的栅格中。

 

        位于栅格(3,3)时地图（左下方为原点，横轴为x轴，纵轴为y轴）的概率分布如下。

 

        现在得到当前时刻的里程计信息如下。

 

       

        我们必须知道里程计工作得多好，例如：

        假设上一时刻完全确定机器人在(3,3)位置，根据里程计信息知道机器人有可能左移1格。而此时有0.5的可能左移1格，有0.2的可能移动到左上角或左下角，有0.1的可能保持不动。

        将这个里程计模型应用到地图中，左移1格后位置为(2,3)。

     

        考虑(3,3)->(2,3) ：

 

        同理，(2,3)->(2,3)：0.1*0.05；(3,2)->(2,3)：0.2*0.18；(3,4)->(2,3)：0.2*0.05。

        所以，当前位置为(2,3)的概率为从所有可能位置移动到(2,3)的后验概率之和。

2.修正

（1）：感知更新前的置信度状态，根据里程计信息更新的后验概率。

（2）：在处获得测量值的概率。关键！取决于传感器的值和预测的上下文。假定环境误差可以用均值描述，任何测量值都不为0。

（3）：传感器（激光）测量值的概率。

   （*）例：

        如果z=1.2m？

      “？”部分（对于超声（而不是激光））：

 

       当测量值固定时可能对应的实际位置的概率的和为1。

       下图为典型的超声（左图）和激光测距仪（右图）测量模型，表示二者测量的距离出现在不同距离值上的概率，虚线表示测量距离，实线表示估计距离。

 

注：翻译选自《COS 495-Lecture 14 Autonomous Robot Navigation》课件。

 

二.Markov定位算法实现

       基于上一节的运动学模型，由于这里在单位时间内对当前位置的周围进行采样，而上一节的模型是对每个位置只是随机采样1点。所以这里假设从上一时刻位置到当前时刻位置的状态转移概率服从高斯分布。根据《Probabilistic Robotics》中的算法：

 

        matlab源码如下：

t=0.4*T;
PosNum=T;                       %number of poses along the route
X=ones(PosNum,1);               %robot pose
DoorPos=[0.3*T,0.4*T,0.7*T];    %door location
DoorNum=size(DoorPos,2);        %number of doors
Cov=30;                         %convariance
Bel=ones(PosNum,1)*1./sum(X);   %uniform initial belief 

Prob=zeros(PosNum,1);           %probability of different poses
for i=1:PosNum
    for j=1:DoorNum
        Prob(i)=Prob(i)+exp(-(i-DoorPos(j))^2/2/Cov);   %assume that looking for doors subjected to normal distributions
    end
end

figure;
set(gcf,'Color','white');
subplot(2,2,1);
i=1:PosNum;
plot(i,Prob(i),'b-');           %p(zt|xt,m)
xlabel('x'); ylabel('p(zt|xt)');
grid on;

for i=1:PosNum
    Bel(i)=Bel(i)*Prob(i);      %bel(x) in figure 7.4(b)
end

%motion model

CurrentPos=t;
ProbMeasure=zeros(PosNum,1);
for i=1:PosNum
    ProbMeasure(i)=exp(-(i-CurrentPos)^2/2/(0.1*Cov));
end

                                %not allowed here! it requires posteriors of all poses per time!
%ProbMeasure=ProbOdom;          %acquire posteriors from motion model and sample only 1 posterior per time
subplot(2,2,2);
i=1:PosNum;
plot(i,ProbMeasure(i),'b-');
xlabel('x'); ylabel('p(xt|xt-1,ut)');
grid on;


%algorithm_markov_localization
BelTemp=zeros(PosNum,1);
for x=1:PosNum
    for i=1:PosNum
        BelTemp(x)=BelTemp(x)+ProbMeasure(i)*Bel(i);
    end
        Bel(x)=Prob(x)*BelTemp(x);
end

for x=1:PosNum
    Bel(x)=Bel(x)/sum(Bel(:));
end

subplot(2,2,3);
i=1:PosNum;
plot(i,Bel(i),'b-');            %desired result is a shifted belief as in figure 7.4(c),but here the experiment result is different  
xlabel('x'); ylabel('bel_mrkv(xt)');
grid on;

for i=1:PosNum
    Bel(i)=Bel(i)*Prob(i);
end
subplot(2,2,4);
i=1:PosNum;
plot(i,Bel(i),'b-');            %bel(x) in figure 7.4(d)
xlabel('x'); ylabel('bel(xt)');
grid on;

 

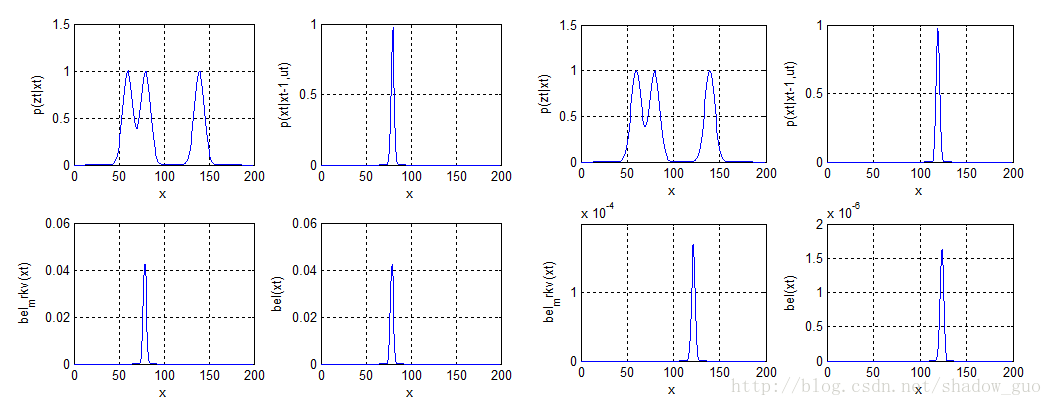
        仿真结果如下图所示：

 

       先说说根据算法实现后上图存在的问题，按书上理想的情况说法，左下图是左上图置信度的右平移，但是这里140附近出现了1个尖峰，甚至高过当前位置的尖峰值。原因是算法的第3行对临时的置信度变量进行累加，造成后面位置的概率累加了前面位置的概率，最终第3行循环结束后出现的结果是个上升的很像Sigmoid函数的曲线，乘以左上图的概率没有办法将140附近的大概率给削弱。如果第3行如书上所说真的是1个平移的置信度曲线，后面的计算得到的曲线则都是合理的。唯一我们不知道的地方是状态转移概率。修改状态转移概率也可以得到合理的结果，这里仅仅是描述过程不再作多余的工作。

      既然状态转移概率有问题那么如前面算法说明那样，强行假设一维运动状态转移概率的结果服从高斯分布，和前面里程计的工作一样，所以只需要将累加的部分给忽略掉。BelTemp为预测部分的结果，修正部分P(z)为常数忽略，由传感器的内部参数决定。

    BelTemp(x)=ProbMeasure(x)*Bel(x);
    Bel(x)=Prob(x)*BelTemp(x);

      maltab仿真结果如下图（左图为机器人在门边，右图为机器人在走廊上）。左图机器人计算得到出现在门边的概率要远大于右图。