主席树学习笔记
问题:给定一个n个数的序列,q次询问第x个数到第y个数中的第k最值。我们假定是第k小。
为了使讨论更加简便,我们假定序列的每个数都是不大于n的正整数。当然一般题目中元素范围很大,但是可以用离散化预处理来做到这一点。
考虑一个比较高端的做法:令g[i][j]为前i个数中,值为j的数的个数。很容易用O(n^2)的代价获得g[ ][ ]数组和其前缀和数组f[ ][ ],其中f[i][j]表示前i个数中,不大于j的数的个数。
注意到第l个数到第r个数中不大于t的数共有f[r][t]-f[l-1][t]个。因此对于每个询问,我们可以二分答案m,比较f[y][m]-f[x-1][m]和k的大小关系。
这个算法比完全暴力要更优,综合时间复杂度为O(n^2+qlogn),可以接受q较大的情况,代码如下:
#include<cstdio>
#include<cstring>
#define rpt(i,l,r) for(i=l;i<=r;i++)
#define N 2015
int a[N];
int p[N][N];
int n,i,j,q,x,y,k,l,r,m,ans;
int main(){
scanf("%d",&n);
memset(p[0],0,sizeof(p[0]));
rpt(i,1,n){
scanf("%d",&a[i]);
rpt(j,1,a[i]-1) p[i][j]=p[i-1][j];
rpt(j,a[i],n) p[i][j]=p[i-1][j]+1;
}
scanf("%d",&q);
while(q--){
scanf("%d%d%d",&x,&y,&k);
l=1;r=n;
while(l<=r){
m=l+r>>1;
if(p[y][m]-p[x-1][m]>=k) ans=m,r=m-1; else l=m+1;
}
printf("%d\n",ans);
}
}
但是这个算法也有缺陷,无法支持n较大的情况。
主席树,全名可持久化线段树。先不要管可持久化是啥,先看线段树。
我学习的时候因为这个迷惑了很久,准确地说,这里是权值线段树。
我们知道,一般的线段树用于维护一个序列a[1...n]的诸多区间问题。在权值线段树中,a[i]表示i这个值出现的次数。
权值线段树一些最基础的应用就是给一个可重数集添加数,删除数,询问第k小,询问排名,等等。
我们先把上文提到的算法中的f数组作一些小变换:因为每个g[i]都是一个一维数组,我们可以将对于每个i,g[i][1...n]这些元素建立一棵线段树。
看上去非常复杂,举个例子画个图冷静一下。设n=4,序列为2,4,1,3,则包括g[0][ ]的g[ ][ ]数组为:
| j=1 | j=2 | j=3 | j=4 | |
| i=1 | 0 | 1 | 0 | 0 |
| i=2 | 0 | 1 | 0 | 1 |
| i=3 | 1 | 1 | 0 | 1 |
| i=4 | 1 | 1 | 1 | 1 |
第一棵:
1[1...4]
/ \
1[1...2] 0[3...4]
/ \ / \
0[1] 1[2] 0[3] 0[4]
第二棵:
2[1...4]
/ \
1[1...2] 1[3...4]
/ \ / \
0[1] 1[2] 0[3] 1[4]
第三棵:
3[1...4]
/ \
2[1...2] 1[3...4]
/ \ / \
1[1] 1[2] 0[3] 1[4]
第四棵:
4[1...4]
/ \
2[1...2] 2[3...4]
/ \ / \
1[1] 1[2] 1[3] 1[4]
我们还是可以秉着二分思想用与前一种算法几乎相同的做法来求取答案,注意到这里二分答案可能会询问到的任何一个值域都一定是线段树的某一整段,因此判断答案是过小还是过大可以做到O(1),因此对于每个询问的复杂度都是O(logn),综合复杂度此时还是O(n^2+qlogn)。
我们发现,这种二分答案做似乎总有一个瓶颈:要统计前若干个数中出现在某值域内的次数,似乎总是需要O(n^2)。真的是这样吗?
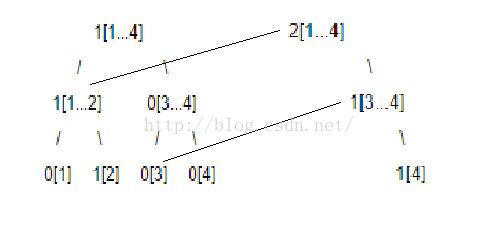
我们观察第一、二棵线段树,发现它们的左子树完全相同。不仅如此,它们的右子树的左子树也是完全相同的。第二、三棵,第三、四棵,甚至是第零、一棵,其中第零棵为结点信息的和值均为0的线段树,都满足只有一条从根到某叶子的链上的各点有区别。显然,不论n有多大,相邻两个线段树中,只有某一条链上的值不同。而线段树的深度当然一定是logn级别的,因此每棵树实际上只有logn个结点是不与前面重复的,既然别的都是重复的,那我们是否可以对每棵树只储存logn级别的结点呢?当然可以!
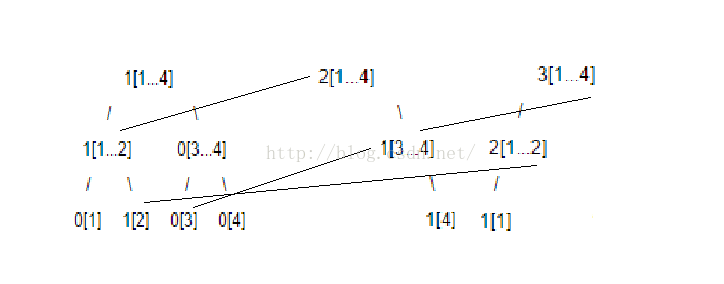
甚至可以这样:
类似这样构造的每棵线段树,即能做到O(nlogn)的代价。因此综合复杂度变为O(nlogn+qlogn),非常优越,代码如下:
#include<cstdio>
#include<cstring>
#define rpt(i,l,r) for(i=l;i<=r;i++)
#define N 100005
int n,cnt,i,a,q,x,y,k;
struct node{
int lb,rb,mid,lc,rc,sum;
}t[N*20];
void build(int x,int l,int r){
t[x].mid=((t[x].lb=l)+(t[x].rb=r))>>1;
t[x].sum=0;
if(l==r) return;
build(t[x].lc=++cnt,l,t[x].mid);
build(t[x].rc=++cnt,t[x].mid+1,r);
}
void ins(int x,int xx,int y){
t[x].mid=((t[x].lb=t[xx].lb)+(t[x].rb=t[xx].rb))>>1;
t[x].sum=t[xx].sum+1;
if(t[x].lb==t[x].rb) return;
if(y>t[x].mid){
t[x].lc=t[xx].lc;
ins(t[x].rc=++cnt,t[xx].rc,y);
}
else{
t[x].rc=t[xx].rc;
ins(t[x].lc=++cnt,t[xx].lc,y);
}
}
int query(int x,int xx,int k){
if(t[x].lb==t[x].rb) return t[x].lb;
int half=t[t[xx].lc].sum-t[t[x].lc].sum;
if(k>half) return query(t[x].rc,t[xx].rc,k-half);
else return query(t[x].lc,t[xx].lc,k);
}
int main(){
//the numbers must be not more than n
scanf("%d",&n);
cnt=n;build(0,1,n);
rpt(i,1,n){
scanf("%d",&a);
ins(i,i-1,a);
}
scanf("%d",&q);
while(q--){
scanf("%d%d%d",&x,&y,&k);
printf("%d\n",query(x-1,y,k));
}
}