hdu 2647 Reward【拓扑排序】

Reward

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 6922    Accepted Submission(s): 2139

Problem Description

Dandelion's uncle is a boss of a factory. As the spring festival is coming , he wants to distribute rewards to his workers. Now he has a trouble about how to distribute the rewards.
The workers will compare their rewards ,and some one may have demands of the distributing of rewards ,just like a's reward should more than b's.Dandelion's unclue wants to fulfill all the demands, of course ,he wants to use the least money.Every work's reward will be at least 888 , because it's a lucky number.

 

 

Input

One line with two integers n and m ,stands for the number of works and the number of demands .(n<=10000,m<=20000)
then m lines ,each line contains two integers a and b ,stands for a's reward should be more than b's.

 

 

Output

For every case ,print the least money dandelion 's uncle needs to distribute .If it's impossible to fulfill all the works' demands ,print -1.

 

 

Sample Input

2 1

1 2

2 2

1 2

2 1

 

 

Sample Output

1777

-1

 

 

Author

dandelion

 

 

Source

曾是惊鸿照影来

 

 题目大意：给你n个人，m个关系，表示a比b的奖金要多。问最少分配的奖金总数是多少。

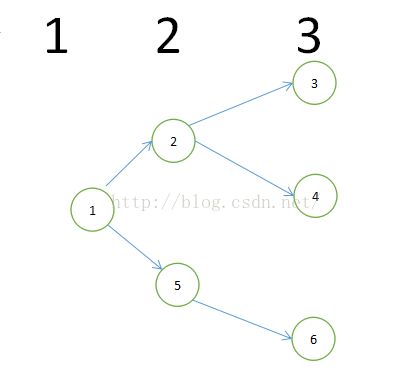
思路：假如有这样一个图：

（ 箭头表示1比2奖金要多，1比5奖金要多）

 不难看出，标号3的那层都是888的奖金，标号2的那层都是889的奖金，标号1的那成是890的奖金，如果我们想要确定每个点权值的话，我们需要知道各个节点之间的全序关系，也就不难想到使用拓扑排序来做这个题，直接能够想到的方法就是直接拆点拆边，完成拓扑排序，如果不满足拓扑序输出-1.那么如果满足拓扑序呢？每个节点拆出来的层数来如何判断呢？每个点权值如何判断呢？这个时候我们其实不用一直憋牛角尖正向思维去做，我们不妨反着来考虑，反向建造图，也就相当于在原图中反着拆点拆边。

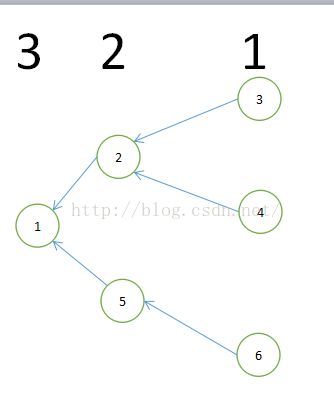
我们将图建成这样：

 这个时候度为0的点也就是分配888奖金的点，也就首先确定了一些点的点权值，接着我们拆边拓扑，也就不难想到，如果当前点u拆边之后使得一个点v的度为0，辣么这个点v的点权值也就比u的点权值多1.这个时候问题就全部解决辣.

最后处理代码问题：

10000*10000的邻接矩阵会超内存，我们使用邻接表实现即可：

#include<stdio.h>
#include<queue>
#include<string.h>
using namespace std;
#define maxn 200010
int head[maxn];
struct EdgeNode
{
    int to;
    int w;
    int next;
} e[maxn];
int vis[maxn];
int price[maxn];
int degree[maxn];
void add(int x,int y,int i)
{
    e[i].to=x;
    e[i].next=head[y];
    head[y]=i;
}
int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        queue<int >s;
        memset(price,0,sizeof(price));
        memset(degree,0,sizeof(degree));
        memset(vis,0,sizeof(vis));
        memset(head,-1,sizeof(head));
        for(int i=0; i<m; i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            degree[x]++;
            add(x,y,i);
        }
        int cont=0;
        for(int i=1;i<=n;i++)
        {
            if(degree[i]==0)
            {
                s.push(i);
                vis[i]=1;
                price[i]=888;
                cont++;
            }
        }
        while(!s.empty())
        {
            int u=s.front();s.pop();
            for(int j=head[u];j!=-1;j=e[j].next)
            {
                int v=e[j].to;
                degree[v]--;
                if(degree[v]==0&&vis[v]==0)
                {
                    vis[v]=1;
                    s.push(v);
                    price[v]=price[u]+1;
                    cont++;
                }
            }
        }
        if(cont==n)
        {
            int sum=0;
            for(int i=1;i<=n;i++)
            {
                sum+=price[i];
            }
            printf("%d\n",sum);
        }
        else
        {
            printf("-1\n");
        }
    }
}