递推求解专题练习（For Beginner） 【hdu】

一定要细心，所有的问题都提交了很多次代码，但是都没有直接AC

long long 定义和输出格式要注意

该题特点，后面的可以根据前面的得出，n限制不大（n越大，往往答案越大），往往案例给出了前几个~（因为让你推的嘛~）

hdu2044

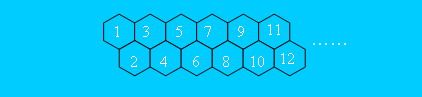
一只小蜜蜂...

Problem Description

有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。

 

Input

输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。

 

Output

对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

 

Sample Input

    
    
    
    

     
     
     
     2
1 2
3 6
    
    
    
    

 

Sample Output

    
    
    
    

     
     
     
     1
3
    
    
    
    

~~~~~~~~~~~~~~~~~~~~~~~~~

题解：每一格的走法都是前两格相加，即f[n]=f[n-1]+f[n-2]

          而两个之间的走法可以转化成从1开始。

#include <cstdio>
#define maxn 55 

long long ans[maxn];

int main(){
	int n,a,b;
	ans[0]=1;
	ans[1]=1;
	ans[2]=1;
	ans[3]=2;
	for(int i =4;i<=50;i++){
		ans[i]=ans[i-1]+ans[i-2];
	}
	scanf("%d",&n);
	while(n--){
		scanf("%d%d",&a,&b);
		printf("%d\n",ans[b-a+1]);
		//注意这里，都可以转化成从1进入。而不是ans[a]-ans[b] 
		
	}
	return 0; 
} 

hdu2045

不容易系列之(3)—— LELE的RPG难题

Problem Description

人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉，这可急坏了众多“Cole”（LELE的粉丝,即"可乐"）,经过多方打探，某资深Cole终于知道了原因，原来，LELE最近研究起了著名的RPG难题:

有排成一行的ｎ个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.

以上就是著名的RPG难题.

如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?

 

Input

输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成，(0<n<=50)。

 

Output

对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。

 

Sample Input

    
    
    
    

     
     
     
     1
2
    
    
    
    

 

Sample Output

    
    
    
    

     
     
     
     3
6
    
    
    
    

题解：

实际上相当于在n-1个块之后再加一个,分两种情况

1.n-1时的首尾相同。则n处直接有2种颜色，而n-1首尾相同的情况就是 f[n-2], 所以是2*f[n-1]

   n-1和1相同，n-1和n-2又肯定不同，所以1和n-2不同，也就和f[n-2]的情况一样了~

2.n-1时的首尾不同。则n处只有一种情况f[n-1]

f[n]=2*f[n-1]+f[n-2]

#include <cstdio>
#define maxn 55

long long ans[maxn];
int main(){
	int n;
	ans[0]=0;
	ans[1]=3;
	ans[2]=6;
	ans[3]=6;
	for(int i = 4;i<=50;i++)
	{
		ans[i]=ans[i-1]+2*ans[i-2];
	} 
	while(scanf("%d",&n)!=EOF&&n){
		printf("%lld\n",ans[n]);
	}
	return 0;
}

hdu2046

骨牌铺方格

Problem Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

 

Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。

 

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

 

Sample Input

    
    
    
    

     
     
     
     1
3
2
    
    
    
    

 

Sample Output

    
    
    
    

     
     
     
     1
3
2
    
    
    
    

网上的解释特别好，直接粘过来了

摘自：http://blog.csdn.net/lishuhuakai/article/details/8531214

  只要简单的推断即可~

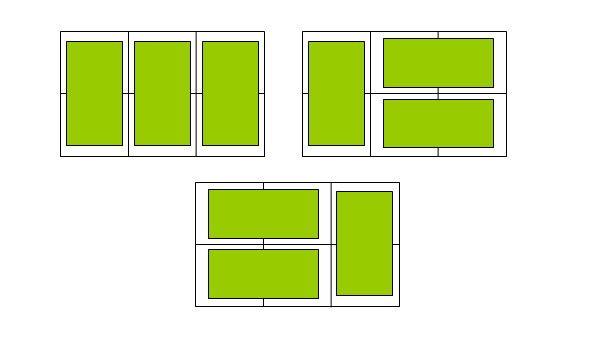
   假设用arr[i]表示2*i的方格一共有组成的方法数，我们知道arr[1]=1;arr[2]=2;

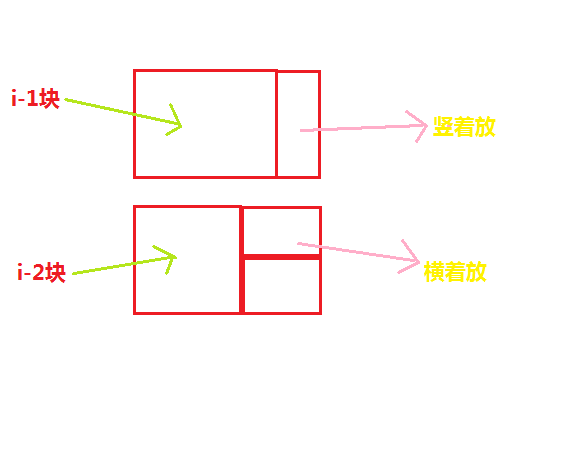
   现在假设我们已经知道了arr[i-1]和arr[i-2],求arr[i],所谓arr[i],不过是在2*（i-1）的格子后边加上一格2*1的方格罢了，骨牌在这一格上横着放，竖着放，如果前面i-1块已经铺好，则第i块只有一种铺法，就是竖着放，如果要横着放，也只有一种铺法，不过要求前面i-2块已经铺好！

 因此arr[i]=arr[i-1]+arr[i-2];

需要特别注意，i-2块之后只能两个横着放，如果竖着放，情况和i-1重复

#include <cstdio>
#define maxn 55

long long ans[maxn];

int main(){
	int n;
	ans[0]=0;
	ans[1]=1;
	ans[2]=2;
	ans[3]=3;
	for(int i=4;i<=50;i++){
		ans[i]=ans[i-1]+ans[i-2];
	}
	while(scanf("%d",&n)!=EOF){
		printf("%lld\n",ans[n]);
	}
	
	return 0;
}

hdu2047

阿牛的EOF牛肉串

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 29149    Accepted Submission(s): 13671

Problem Description

今年的ACM暑期集训队一共有18人，分为6支队伍。其中有一个叫做EOF的队伍，由04级的阿牛、XC以及05级的COY组成。在共同的集训生活中，大家建立了深厚的友谊，阿牛准备做点什么来纪念这段激情燃烧的岁月，想了一想，阿牛从家里拿来了一块上等的牛肉干，准备在上面刻下一个长度为n的只由"E" "O" "F"三种字符组成的字符串（可以只有其中一种或两种字符，但绝对不能有其他字符）,阿牛同时禁止在串中出现O相邻的情况，他认为，"OO"看起来就像发怒的眼睛，效果不好。

你，NEW ACMer,EOF的崇拜者，能帮阿牛算一下一共有多少种满足要求的不同的字符串吗？

PS: 阿牛还有一个小秘密，就是准备把这个刻有 EOF的牛肉干，作为神秘礼物献给杭电五十周年校庆，可以想象，当校长接过这块牛肉干的时候该有多高兴！这里，请允许我代表杭电的ACMer向阿牛表示感谢！

再次感谢！

 

Input

输入数据包含多个测试实例,每个测试实例占一行,由一个整数n组成，(0<n<40)。

 

Output

对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。

 

Sample Input

   
   
   
   

    
    
    
    1
2
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    3
8
   
   
   
   

题解：

根据n-1的结尾分两种情况

理解角度一：

1.n是E,F，不管n-1是什么情况都可以接，即2*f[n-1]

2.n是O，那么只有n-1不是O的时候可以，也就是n-1的情况1 ，也就是2*f[n-2]

f[n]=2*f[n-1]+2*f[n-2];

理解角度二：

设S[n]为n个字符，结尾是O 的情况，T[n]结尾是E.F的情况

1.n-1是O,n只能是E/F，2*S[n-1];

2.n-1是E/F，n可以为任意，3*T[n-1]

f[n]=2*S[n-1]+3*T[n-1]=2*f[n-1]+T[n-1]

T[n-1]实际上就是n-2时候以E/F结尾，2*f[n-2]

所以f[n]=2*f[n-1]+2*f[n-2];

#include <cstdio>
#define maxn 55

long long ans[maxn];

int main(){
	int n;
	ans[0]=0;
	ans[1]=3;
	ans[2]=8;
	for(int i=3;i<=50;i++){
		ans[i]=2*(ans[i-1]+ans[i-2]);
	}
	while(scanf("%d",&n)!=EOF){
		printf("%lld\n",ans[n]);
	}
	
	return 0;
}

hdu2048

神、上帝以及老天爷

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 31748    Accepted Submission(s): 13035

Problem Description

HDU 2006'10 ACM contest的颁奖晚会隆重开始了！
为了活跃气氛，组织者举行了一个别开生面、奖品丰厚的抽奖活动，这个活动的具体要求是这样的：

首先，所有参加晚会的人员都将一张写有自己名字的字条放入抽奖箱中；
然后，待所有字条加入完毕，每人从箱中取一个字条；
最后，如果取得的字条上写的就是自己的名字，那么“恭喜你，中奖了！”

大家可以想象一下当时的气氛之热烈，毕竟中奖者的奖品是大家梦寐以求的Twins签名照呀！不过，正如所有试图设计的喜剧往往以悲剧结尾，这次抽奖活动最后竟然没有一个人中奖！

我的神、上帝以及老天爷呀，怎么会这样呢？

不过，先不要激动，现在问题来了，你能计算一下发生这种情况的概率吗？

不会算？难道你也想以悲剧结尾？！

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(1<n<=20),表示参加抽奖的人数。

 

Output

对于每个测试实例，请输出发生这种情况的百分比，每个实例的输出占一行, 结果保留两位小数(四舍五入)，具体格式请参照sample output。

 

Sample Input

   
   
   
   

    
    
    
    1
2
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    50.00%
   
   
   
   

题解，也可以看成n-1后又有一个人

1.n-1个人都不一样，来第n个人，n和其中一个人交换   (n-1)*f(n-1)

2.n-1中有一个人拿自己的，来n个人，和他交换。n-1中有一个人拿自己的情况是f[n-2]，所以是：(n-1)*f[n-2]

f[n]=(n-1)*(f[n-1]+f[n-2]);

#include <cstdio>
#define maxn 22

long long ans[maxn],b[maxn];

int main(){
	int n,k;
	ans[0]=0;ans[1]=0;ans[2]=1;
	b[0]=0;	b[1]=1;b[2]=2;
	for(int i=3;i<=20;i++){
		b[i]=i*b[i-1];
		ans[i]=(i-1)*(ans[i-1]+ans[i-2]);
	}
	scanf("%d",&k); 
	while(k--){
	 	scanf("%d",&n); 
		printf("%.2f%%\n",ans[n]*100.0/b[n]);
	}
	
	return 0;
}